在这一页
解构阿特金斯饮食老虎机
介绍
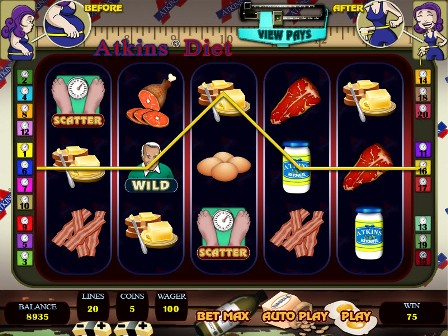
2008年,我在澳大利亚悉尼的一个老虎机会议上做了一个演讲,设计了阿特金斯饮食法老虎机。当时,我用它来演示视频老虎机(有时也被称为pokies)的设计。我会先介绍一下它的赔率表和转轴条,然后再展示各种赢钱方式的概率和回报率。
赔率表
下表为阿特金斯饮食法赔付表。所有奖金必须左对齐。阿特金斯符号为百搭符号,可替代除体重秤以外的任何符号。
阿特金斯饮食支付表
| 象征 | 连续 5 次 | 连续4次 | 连续 3 次 | 连续 2 次 |
|---|---|---|---|---|
| 阿特金斯 | 5000 | 500 | 50 | 5 |
| 牛排 | 1000 | 200 | 40 | 3 |
| 火腿 | 500 | 150 | 三十 | 2 |
| 布法罗鸡翅 | 300 | 100 | 二十五 | 2 |
| 香肠 | 200 | 75 | 20 | 0 |
| 鸡蛋 | 200 | 75 | 20 | 0 |
| 黄油 | 100 | 50 | 15 | 0 |
| 奶酪 | 100 | 50 | 15 | 0 |
| 熏肉 | 50 | 二十五 | 10 | 0 |
| 蛋黄酱 | 50 | 二十五 | 10 | 0 |
卷轴条
以下是阿特金斯饮食法的卷轴。
阿特金斯饮食卷条
| 停止 | 卷轴 1 | 卷轴 2 | 卷轴 3 | 卷轴 4 | 卷轴 5 |
|---|---|---|---|---|---|
| 1 | 规模 | 蛋黄酱 | 火腿 | 火腿 | 熏肉 |
| 2 | 蛋黄酱 | 布法罗鸡翅 | 黄油 | 奶酪 | 规模 |
| 3 | 火腿 | 牛排 | 鸡蛋 | 阿特金斯 | 牛排 |
| 4 | 香肠 | 香肠 | 规模 | 规模 | 火腿 |
| 5 | 熏肉 | 奶酪 | 奶酪 | 黄油 | 奶酪 |
| 6 | 鸡蛋 | 蛋黄酱 | 蛋黄酱 | 熏肉 | 香肠 |
| 7 | 奶酪 | 火腿 | 黄油 | 奶酪 | 黄油 |
| 8 | 蛋黄酱 | 黄油 | 火腿 | 香肠 | 熏肉 |
| 9 | 香肠 | 熏肉 | 香肠 | 牛排 | 布法罗鸡翅 |
| 10 | 黄油 | 牛排 | 熏肉 | 鸡蛋 | 奶酪 |
| 11 | 布法罗鸡翅 | 香肠 | 牛排 | 熏肉 | 香肠 |
| 12 | 熏肉 | 蛋黄酱 | 布法罗鸡翅 | 蛋黄酱 | 火腿 |
| 十三 | 鸡蛋 | 火腿 | 黄油 | 香肠 | 黄油 |
| 14 | 蛋黄酱 | 阿特金斯 | 蛋黄酱 | 奶酪 | 牛排 |
| 15 | 牛排 | 黄油 | 奶酪 | 黄油 | 蛋黄酱 |
| 16 | 布法罗鸡翅 | 鸡蛋 | 香肠 | 火腿 | 鸡蛋 |
| 17 | 黄油 | 奶酪 | 鸡蛋 | 蛋黄酱 | 香肠 |
| 18 | 奶酪 | 熏肉 | 熏肉 | 熏肉 | 火腿 |
| 19 | 鸡蛋 | 香肠 | 蛋黄酱 | 布法罗鸡翅 | 阿特金斯 |
| 20 | 阿特金斯 | 布法罗鸡翅 | 布法罗鸡翅 | 香肠 | 黄油 |
| 21 | 熏肉 | 规模 | 火腿 | 奶酪 | 布法罗鸡翅 |
| 22 | 蛋黄酱 | 蛋黄酱 | 香肠 | 鸡蛋 | 蛋黄酱 |
| 23 | 火腿 | 黄油 | 熏肉 | 黄油 | 鸡蛋 |
| 24 | 奶酪 | 奶酪 | 奶酪 | 布法罗鸡翅 | 火腿 |
| 二十五 | 鸡蛋 | 熏肉 | 鸡蛋 | 熏肉 | 熏肉 |
| 二十六 | 规模 | 鸡蛋 | 阿特金斯 | 蛋黄酱 | 黄油 |
| 二十七 | 黄油 | 布法罗鸡翅 | 布法罗鸡翅 | 鸡蛋 | 牛排 |
| 二十八 | 熏肉 | 蛋黄酱 | 熏肉 | 火腿 | 蛋黄酱 |
| 二十九 | 香肠 | 牛排 | 黄油 | 香肠 | 香肠 |
| 三十 | 布法罗鸡翅 | 火腿 | 奶酪 | 牛排 | 鸡蛋 |
| 31 | 牛排 | 奶酪 | 蛋黄酱 | 蛋黄酱 | 奶酪 |
| 三十二 | 黄油 | 熏肉 | 牛排 | 熏肉 | 布法罗鸡翅 |
示例旋转
让我们看看下面的旋转示例。
多线视频老虎机的工作原理是为每个转轴选择一个随机数,并将其映射到转轴条上相应的停止位置。假设所选的随机数指定了转轴在中间行的停止位置。上方和下方的符号将是转轴条上正上方和正下方的符号。
如果1至5号转轴分别出现27、14、3、31和27的随机数,则会出现上述结果。下表显示了所有15个可见符号在屏幕上的转轴条位置。
阿特金斯饮食卷条
| 停止 | 卷轴 1 | 卷轴 2 | 卷轴 3 | 卷轴 4 | 卷轴 5 |
|---|---|---|---|---|---|
| 顶部 | 二十六 | 十三 | 2 | 三十 | 二十六 |
| 中间 | 二十七 | 14 | 3 | 31 | 二十七 |
| 底部 | 二十八 | 15 | 4 | 三十二 | 二十八 |
还要注意的是,卷轴上的条带是环绕的。因此,如果中间位置选择的数字是 1,那么顶部位置的数字就是 32。同样,如果中间位置的数字是 32,那么底部位置的数字就是 1。
符号分布
计算视频老虎机回报率的第一步是计算每个符号在每个转轴上出现的频率。下表解答了这个问题。
阿特金斯饮食符号分布
| 象征 | 卷轴 1 | 卷轴 2 | 卷轴 3 | 卷轴 4 | 卷轴 5 |
|---|---|---|---|---|---|
| 阿特金斯 | 1 | 1 | 1 | 1 | 1 |
| 牛排 | 2 | 3 | 2 | 2 | 3 |
| 火腿 | 2 | 3 | 3 | 3 | 4 |
| 布法罗鸡翅 | 3 | 3 | 3 | 2 | 3 |
| 香肠 | 3 | 3 | 3 | 4 | 4 |
| 鸡蛋 | 4 | 2 | 3 | 3 | 3 |
| 黄油 | 4 | 3 | 4 | 3 | 4 |
| 奶酪 | 3 | 4 | 4 | 4 | 3 |
| 熏肉 | 4 | 4 | 4 | 5 | 3 |
| 蛋黄酱 | 4 | 5 | 4 | 4 | 3 |
| 规模 | 2 | 1 | 1 | 1 | 1 |
| 全部的 | 三十二 | 三十二 | 三十二 | 三十二 | 三十二 |
线路支付数学
阿特金斯饮食法共有 32 × 32 × 32 × 32 × 32 = 33,554,432 种可能的结果。下表显示了每种可能的组合中有多少种结果能够获胜。这些数字是由一个包含五个嵌套循环的程序计算得出的,该程序会统计每种可能组合的获胜总数。
阿特金斯饮食线支付组合
| 象征 | 连续 5 次 | 连续4次 | 连续 3 次 | 连续 2 次 | 全部的 |
|---|---|---|---|---|---|
| 阿特金斯 | 1 | 二十八 | 513 | 1,024 | 1,566 |
| 牛排 | 431 | 2,996 | 32,480 | 326,656 | 362,563 |
| 火腿 | 955 | 5,157 | 42,112 | 315,392 | 363,616 |
| 布法罗鸡翅 | 764 | 5,348 | 58,464 | 430,080 | 494,656 |
| 香肠 | 1,595 | 8,613 | 54,432 | - | 64,640 |
| 鸡蛋 | 956 | 6,692 | 52,864 | - | 60,512 |
| 黄油 | 1,995 | 10,692 | 88,704 | - | 101,391 |
| 奶酪 | 1,996 | 13,860 | 85,536 | - | 101,392 |
| 熏肉 | 2,976 | 20,832 | 103,168 | - | 126,976 |
| 蛋黄酱 | 2,980 | 20,860 | 128,736 | - | 152,576 |
| 全部的 | 14,649 | 95,078 | 647,009 | 1,073,152 | 1,829,888 |
下表显示了每种可能中奖的概率。该概率是用上表所示的中奖组合数除以组合总数 33,554,432 得出的。右下角单元格中的总数反映了每行的中奖频率(即中奖概率)为 5.45%。
阿特金斯线支付概率
| 象征 | 连续 5 次 | 连续4次 | 连续 3 次 | 连续 2 次 | 全部的 |
|---|---|---|---|---|---|
| 阿特金斯 | 0.00000003 | 0.00000083 | 0.00001529 | 0.00003052 | 0.00004667 |
| 牛排 | 0.00001284 | 0.00008929 | 0.00096798 | 0.00973511 | 0.01080522 |
| 火腿 | 0.00002846 | 0.00015369 | 0.00125504 | 0.00939941 | 0.01083660 |
| 布法罗鸡翅 | 0.00002277 | 0.00015938 | 0.00174236 | 0.01281738 | 0.01474190 |
| 香肠 | 0.00004753 | 0.00025669 | 0.00162220 | - | 0.00192642 |
| 鸡蛋 | 0.00002849 | 0.00019944 | 0.00157547 | - | 0.00180340 |
| 黄油 | 0.00005946 | 0.00031865 | 0.00264359 | - | 0.00302169 |
| 奶酪 | 0.00005949 | 0.00041306 | 0.00254917 | - | 0.00302172 |
| 熏肉 | 0.00008869 | 0.00062084 | 0.00307465 | - | 0.00378418 |
| 蛋黄酱 | 0.00008881 | 0.00062168 | 0.00383663 | - | 0.00454712 |
| 全部的 | 0.00043657 | 0.00283355 | 0.01928237 | 0.03198242 | 0.05453491 |
下表显示了每种可能的中奖方式对回报的贡献。每个单元格是上表中概率与赔付表的乘积。右侧单元格显示线赔付的总回报率为 63.46%。
阿特金斯饮食法预期收益
| 象征 | 连续 5 次 | 连续4次 | 连续 3 次 | 连续 2 次 | 全部的 |
|---|---|---|---|---|---|
| 阿特金斯(野生) | 0.000149 | 0.000417 | 0.000764 | 0.000153 | 0.001483 |
| 牛排 | 0.012845 | 0.017858 | 0.038719 | 0.029205 | 0.098627 |
| 火腿 | 0.014231 | 0.023054 | 0.037651 | 0.018799 | 0.093734 |
| 布法罗鸡翅 | 0.006831 | 0.015938 | 0.043559 | 0.025635 | 0.091963 |
| 香肠 | 0.009507 | 0.019252 | 0.032444 | - | 0.061202 |
| 鸡蛋 | 0.005698 | 0.014958 | 0.031509 | - | 0.052165 |
| 黄油 | 0.005946 | 0.015932 | 0.039654 | - | 0.061532 |
| 奶酪 | 0.005949 | 0.020653 | 0.038238 | - | 0.064839 |
| 熏肉 | 0.004435 | 0.015521 | 0.030746 | - | 0.050702 |
| 蛋黄酱 | 0.004441 | 0.015542 | 0.038366 | - | 0.058349 |
| 全部的 | 0.070029 | 0.159124 | 0.331651 | 0.073792 | 0.634597 |
分散支付
秤盘用作分散支付符号。只要分散支付符号出现在屏幕上的任何位置,玩家即可获得奖励。与线支付不同,分散支付符号无需左对齐或位于有效支付线上。公平起见,分散支付的赢利取决于总投注金额。下表显示了每卷轴上的分散支付符号数量、每卷轴上的符号总数以及分散支付在该卷轴上的概率,即 3×(第 2 列)/(第 3 列)。乘以 3 的原因是每个卷轴上有三个可见位置。
每卷阿特金斯饮食散布
| 卷轴 | 散点图 | 总符号数 在卷轴上 | 分散 可能性 |
|---|---|---|---|
| 1 | 2 | 三十二 | 0.18750 |
| 2 | 1 | 三十二 | 0.09375 |
| 3 | 1 | 三十二 | 0.09375 |
| 4 | 1 | 三十二 | 0.09375 |
| 5 | 1 | 三十二 | 0.09375 |
下表显示了分散符号总数为0至5个时,其概率及其对回报的贡献。右下角单元格显示,分散支付功能为游戏回报贡献了6.98%。
阿特金斯饮食分散支付概率和回报
| 散点图 | 支付 | 组合 | 可能性 | 返回 |
|---|---|---|---|---|
| 5 | 100 | 486 | 0.000014 | 0.001448 |
| 4 | 二十五 | 20,898 | 0.000623 | 0.015570 |
| 3 | 5 | 353,916 | 0.010548 | 0.052738 |
| 全部的 | 33,554,432 | 0.011185 | 0.069756 |
奖金
玩家至少获得三个分散的刻度即可获得奖励。上表中3至5个刻度的概率之和为0.011185。奖励期间,玩家将获得十次免费旋转,所有奖金将增加三倍。
在此游戏中,免费旋转使用与基础游戏相同的卷轴。我们已经显示,预期线支付回报为 0.634597,预期分散回报为 0.069756。因此,如果奖金增加三倍,则每转预期奖金为 3 × (0.634597 + 0.069756) = 2.113058。
接下来,有一条规则:免费旋转可以无限次获得。奖励中预期的总旋转次数为 10/(1-10×0.011185) = 11.259335。
因此,有 11.259335 次免费旋转,每次旋转的平均赢额为 2.113058,每个奖金的预期最终赢额为 11.259335 × 2.113058 = 23.791632。
首先赢得奖金的概率是 0.011185,因此奖金功能每次初始旋转的预期回报是 0.011185 × 23.791632 = 0.266105。
概括
下表总结了游戏中三种获胜方式。右下角单元格显示预期回报率为 97.046%。换句话说,玩家每投注 1 美元,预期可获得 97 美分的回报。
阿特金斯饮食总结
| 物品 | 返回 |
|---|---|
| 线路支付 | 63.460% |
| 分散 | 6.976% |
| 奖金 | 26.610% |
| 全部的 | 97.046% |
更多解构
我拆解过很多老虎机。以下是一些例子:
- 解构视频老虎机的 Jackpot Party分析。
- 解构经典米高梅渐进式游戏的狮子份额分析。
- 解构流行的 IGT 游戏的埃及艳后分析。
- 解构 Lionfish对许多 Game Maker 机器上的老虎机游戏的分析。
- 解构 Megabucks 。
- 解构阿特金斯饮食法老虎机。
- 解构幸运拉里的龙虾狂热。
- 解构 Hexbreaker 。
- 解构 Blazing Sevens 。
- 解构热卷。
内部链接
- 玩阿特金斯饮食法。您可以玩演示版来获得乐趣。
- 解构阿特金斯饮食老虎机。本页早期的 PDF 版本。
- 老虎机主页。
- 附录 4显示了如何计算我的Wizard's Fruit Slot Machine的回报。
- 附录5 21铃老虎机分析。
- 附录6红、白、蓝老虎机分析。
- 对北卡罗来纳州的基于技能的老虎机进行锁定和滚动分析。