轮盘 - 常问问题
如果你这样玩轮盘赌会怎么样——在0和00各押5美元,再在任意两列各押15美元。这样你赢的概率不是有70%左右吗?
你将拥有2/38的概率赢得140美元,24/38的概率赢得5美元,以及12/38的概率损失40美元。总体预期回报率为[(2/38)*140 + (24/38)*5 + (12/38)*-40]/40 = -5.26%。这与双零轮盘赌中每次投注的庄家优势相同(除了0-00-1-2-3组合,其庄家优势为7.89%)。
假设我走进一家赌场,在轮盘赌的赔率2-1中押注两个,比如押1-12的100美元,押13-24的100美元。如果是一次性交易,我赢100美元的概率难道不是63%吗?我不是说长期来看,只是一次性的赌注。
你说得对,中奖概率是24/38,也就是大约63%。然而,你得冒200美元的风险,才能赢100美元。如果你想进一步提高中奖概率,那就押注任意35个号码。中奖概率将达到92%。
轮盘赌中有没有组合投注来最大化赔率的方法?例如,12 的赔率为 2 比 1。如果我下注 22,比如第一组和第二组都是 12,那么我有 63.16% 的概率赢钱。这比简单的红/黑、单/偶或高/低投注要好。虽然我实际上的赔率只有 1 比 1,而不是 2 比 1(如果我赢了,因为中奖号码不能同时出现在第一组和第二组 12 中,所以我的部分投注必须输掉),但通过组合两个投注,赔率略微对我有利。这类组合的赔率已经确定了吗?如果已经确定了,我可以在哪里找到它们?
只要你避开0-0-0-1-2-3的组合,任何投注组合的赌场优势始终是1/19,即5.26%。有一些方法可以提高你的赢钱概率,但代价是赢钱金额相对于你的总投注金额会减少。
昨晚我玩轮盘赌,用的是“马丁格尔”策略,第一次输了之后就加倍两次。我知道这很蠢,但我通常输得不多,而且赌的时间很长。总之,我之所以输掉这局,是因为我押注相同,结果四次投掷,有三次都出现了数字9。这概率有多大?听起来可疑吗?话说回来,赌场有没有被发现作弊?
4次中任意三次出现任意数字的概率是38*4*(1/38) 3 *(37/38) = 1/5932。然而,如果你玩得够久,几乎会忍不住注意到类似的异常情况。这远不至于引起怀疑。在现实赌场中确实存在作弊行为。通常情况下,被赌场保安抓到的都是不法荷官。虽然有一些针对在线赌场的作弊案件,但据我所知,还没有政府机构判处任何人有罪。
像大多数玩家那样,在一次投注中同时投注多个内圈号码(而非连续投注一个号码),难道不是更糟糕的轮盘投注策略吗?例如,假设你手上有 100 美元,那么在“8”这个数字上投注 10 次,每次 10 美元,比在一次投注 10 个号码上投注 10 美元损失更小吗?在我看来,“对冲”只是保证某些投注(在上面的例子中是 9 次)总是会输吗?你的页面上没有提到“对冲”吗?
请参阅我的《赌博十诫》 。第六诫是“切勿两面下注”。关于您的轮盘赌问题,如果一次只押一个数字,则输掉所有十个数字的概率为 (37/38) 10 = 76.59%。如果一次性将十个数字押在不同数字上,则输掉所有十个数字的概率为 (28/38) = 73.68%。通过对冲,即一次性押注十个数字,您可以降低全输的概率,但也将最高赢利限制在 26 美元。如果一次押一个数字,则最高赢利可达 350 美元。这两种方法的总预期回报率相同,均为 94.74%。
我读过你关于系统的页面,而且多年来一直跟别人讲这个!我在赌场发轮盘,各种系统我都见过。我见过一个系统,虽然在电脑模拟中可能行不通(很可能永远行不通),但在现实生活中却“似乎”行得通。也就是说,我看到它赢的次数比输的次数多。
它的运作方式是,玩家在1到18的数字上投注75美元,在第三个12的数字上投注50美元,在0到00的数字上投注10美元,总共135美元。这涵盖了除六个数字(19到22)之外的所有数字,并且每次球未击中这六个数字时,都会产生15美元的赔付,除非击中0或00,在这种情况下,赔付40美元。我知道这听起来很疯狂!!!但相信我,我可以告诉你,我见过用这种方法赢的比输的多。反过来也一样(废话)。我很想知道这个系统的真实赔率,但当有人从我的桌子上赚了2000美元时,很难告诉他它不起作用:-)
有30种方式可以赢得15美元,有6种方式可以输掉135美元,还有2种方式可以赢得45美元(而不是40美元)。这种投注组合的预期回报为((30/38)*15 + (6/38)*-135 + (2/38)*(45))/135 = -0.0526,即5.26%,只要避免可怕的0-0-0-1-2-3组合,任何一种投注或投注组合的赌场优势就为5.26%。在你的观察中,你可能看到的出现次数比预期的要少,只有19-24次,这解释了为什么你会误以为这种方法会赢。
巫师,我在想轮盘赌的事。用Boss Media软件,你可以不用下注就能转动轮盘。这难道不是对玩家有利吗?我见过的一些轮盘投注系统,比如马丁格尔系统,输了就翻倍等等。难道你不能只看着轮盘不下注,然后根据之前的旋转结果来下注吗?举个例子,在下注之前先转5圈。假设所有数字都是奇数,一开始就押偶数不是更合理吗?我知道这有点儿像赌徒谬误,轮盘不在乎上次旋转的结果,而且每次旋转后,奇数出现的概率都会减小。我是不是明白了什么道理,还是只是在重复一个老理论?
你只是在重复赌徒谬误。如果球在一个公平的轮盘上连续100次落在奇数位置,那么下一轮是偶数的概率仍然和每次一样,在双零轮盘上是47.37%。所以,即使你不用下注也能旋转,这根本没用。球没有记忆。
虽然轮盘赌显然不可能靠运气取胜,但我听说理论上可以通过两种物理原理取胜。方法一:使用高科技设备,测量球的速度与轮盘速度的对比,并以大约40%的准确率预测轮盘的结果区域。方法二:轮盘偏差。显然,轮盘的偏差至少要达到5.26%才能让玩家保持平衡。问题是,巫师,您觉得需要旋转多少次才能确定轮盘偏差(如果有的话)?
我听说过这两种伎俩都被用过。我对计时轮盘的装置了解不多,只知道它们确实存在,而且时不时有人使用。在内华达州,这种装置是绝对违法的。我听说利用有偏差的轮盘作案的案例更多,而且这种事已经发生过很多次了。我认为使用老式轮盘的赌场是最容易被利用的目标。多年来我一直在说,我认为阿根廷就是一个成熟的目标。
在任何一个均等赔率的轮盘上,用马丁格尔双倍投注系统对抗单零轮盘时,我估计你每248次投注中会输一次。也就是说,一个投注要么赢一个单位,要么输255个单位。我的计算正确吗?如果不正确,能否请您给出正确的赔率?
如果最大损失为255个单位,那么您最多可以下注8次。连续输掉8次的概率为(19/37) 8 = 0.004835。因此,您赢得一个单位的概率为99.52%,输掉255个单位的概率为0.48%。
平均而言,在单零轮盘赌中,在 36 次旋转过程中,一个数字会重复多少次(例如连续两个 8)?
每 37 对数字中,预期会出现一次重复。所以,36 个数字对应 35 对数字。因此,预期重复次数为 35/37 = 0.9459。
大家都说,从长远来看,用数学系统是赢不了轮盘赌的。但是,你该如何解释为什么有些职业赌徒靠轮盘赌谋生呢?我认为这并非吹牛。他们每天玩轮盘赌,实际上赢的比输的要多。
告诉我谁在公平的轮盘赌中赢钱,我就能告诉你谁只是运气好,很可能会输光所有钱。你只有巧妙地利用优势才能在轮盘赌中获胜,比如利用有偏差的轮盘,或者精准地控制轮盘。
我读了你所有关于轮盘赌的内容,但没看到任何关于轮盘转盘机的内容。在赌场经理的密切关注下,轮盘转盘机抛出“部分”来提高赌场的胜率。那些能抛出绿色的转盘机,虽然不是每次都能,但概率很高,当他想彻底消灭一个大额累积奖金玩家时,大概七八次就能抛出一次。
赌场无需诉诸此类策略即可赢钱。此外,赌场无需惧怕累积奖金玩家。大多数累积奖金玩家都能赢钱,但少数达到资金上限的玩家会为所有赢家支付赔款,赌场还会因此损失一部分。此外,要故意将球旋转到特定区域需要高超的技巧。我认为,这很难做到非常精准。
嗨,巫师,您的网站太棒了。在双0轮盘赌中,我意识到所有投注都有同样高的赌场优势,但我刚刚完成一门统计学课程,我发现由于标准差的存在,并非所有投注都完全相同。例如,根据我的计算,1美元投注红色,其标准差为1.012019,而1美元投注单个数字,其标准差为5.839971。因此,在1次、100次和10000次试验中,等额投注的预期胜出概率分别为0.4793、0.3015和0.0000,而单个数字投注的预期胜出概率分别为0.4964、0.4641和0.1837。我的分析正确吗?(我假设了正态分布)谢谢!
谢谢你的赞美。首先,任何等额投注的标准差是0.998614,单个数字的标准差是5.762617。在1、100和10000次旋转中,通过等额投注平注获胜的概率分别为0.473684、0.265023和0.00000007。在1、100和10000次旋转中,通过单个数字平注获胜的概率分别为0.0263158、0.491567和0.18053280。你似乎想说,单个数字投注更好,因为其获胜的概率高于多个投注。这话没错,但是,巨额亏损的概率也更大。在一个回合中,预期结果总是落在钟形曲线的某个位置。对于低波动性投注(例如红色或黑色),钟形曲线很陡峭,不会偏离小额亏损太远。对于高波动性投注(例如单个数字),钟形曲线很宽,允许更大的净结果范围,包括好结果和坏结果。
我的同事 D. 坚持说他已经找到了一种在轮盘赌中持续获胜的完美方法。我不太信服。他是运气好,还是有什么有效的方法?
他只是运气好而已。我已经说过无数次了,没有任何投注系统能够经得起时间的考验。
我读了你在轮盘赌中关于马丁格尔方法的文章。我在电脑上试过几次这种方法,赢了500美元。然后我去了赌场,输了1000多美元。因为黑牌连续出现了8次。但我才刚开始学习百家乐。我之前在电脑上试过,也赢了500美元,因为我押庄。一开始是20美元,然后是40美元,然后是80美元,以此类推。即使每手牌都要支付5%的佣金,我也赢了500美元。你觉得这种方法在赌场行得通吗?我想在去赌场再输1000美元之前问问。就像我说的,黑牌连续出现了8次。但你觉得闲家会连续赢8次吗?而且,百家乐很好玩,因为平局算输,而在轮盘赌中,0或00算输。
马丁格尔策略在每场游戏中都存在风险,长远来看永远不会赢。然而,由于赌场优势较低,它在百家乐中比在轮盘赌中更适用。玩家连续赢8次的概率是0.493163^8 = 286分之一。另外,请记住,你可能在系列赛后期赢了一手牌,但仍然会因为佣金而落后。例如,如果你最初下注1美元,在第7手牌赢了,你将赢得60.80美元(64美元*95%),这不足以弥补之前输掉的63美元。
你好。你说所有投注系统都会失效。如果你玩轮盘赌,在1-12号投注一个单位,在13-24号投注两个单位,那么你赢钱或不赢钱的概率是不是有66.66%?
不完全是。您有 12/38 的概率赢得 3 个单位,12/38 的概率不赢不赔,14/38 的概率输掉 3 个单位。预期值为 [(12/38)*3 + (12/38)*0 + (14/38)*-3]/3 = (-6/38)/3 = -2/38 = -5.26%。任何投注组合都适用,只要您避开可怕的 5 个数字组合 (0/00/1/2/3)。如果您只玩一轮,并且想要最大化您的获胜概率,那么请在 35 个数字上均等投注。您有 92.11% 的概率赢得 1 个单位,7.89% 的概率输掉 35 个单位。
你好。我玩轮盘赌已经好几年了,这是我第一次考虑尝试轮盘赌系统……现在我知道你对这些所谓的“系统”以及它们背后的骗子是什么感觉了。相信我,我也有同样的感受,但我遇到过两个不容忽视的系统……
第一个是 RD Ellison 著作《赌赢:轮盘》中的 3q/A 策略,其验证胜率为 7.94%(7500 次旋转)。该系统由 Frank Scoblete 的《Spin roultte Gold》和 Eric St. Germain 的《轮盘系统测试员》共同测试和开发。
第二个是 Don Young 的轮盘系统,该系统经过验证,击败了 Zumma Publishing 的轮盘系统测试仪(15000 次旋转)。
现在,我必须得说,我对花钱购买这些系统还是有点怀疑,但既然它们已经经过长期考验,我实在找不到不买的理由。我的意思是,打败这些考试题库肯定意味着什么……
你对这些系统有什么看法?你觉得我应该尝试一下吗?
非常感谢!祝您今天愉快。祝一切顺利
7500次旋转?就这些吗?如果下注积极,任何人都可以在7500次旋转中获得相当于总投注金额7.94%的利润。15000次旋转也是如此。大多数系统的设计初衷就是为了获得大量小额收益和少量巨额亏损。一个需要巨额资金的系统很容易在15000次旋转后就盈利。但最终亏损会接踵而至,它经不起时间的考验。巨额亏损也可能在一开始就出现。检验一个系统的真正方法是进行数十亿次的试验。我对这些系统的看法和所有系统一样,它们一文不值。我不介意你尝试一下,但我不介意有人把一分钱塞进卖主的口袋里。
注:请参阅下一栏中对此问题的后续内容。
尊敬的先生,在单零轮盘游戏中,如果您在更多次旋转中将部分资金押在较少的数字上,而不是每次旋转都押在更多数字上,那么您获胜的概率就会增加。例如:如果您愿意冒 500 美元的风险赢得 250 美元,那么您可以:选项 (A):在两打中的任意一打上押 250 美元,如果您赢了,您将赢得 250 美元。发生这种情况的概率是 24/37=(0.648648)。选项 (B):在任意一打上押 125 美元,如果您赢了,您将赢得 250 美元并离开。但是,如果您输了,您现在可以在同一个打上押 187.5 美元,如果您赢了,您将赢得 375 美元,这将使您获得 250 美元以及您在上一次旋转中输掉的 125 美元。现在,即使两次都输了,您仍然有 187.5 美元可用,您可以在任意九个数字上投注 20.833333 美元,如果您赢了,您将获得 750 美元,这相当于您的 500 美元原始资金加上您的目标奖金 250 美元。这种情况发生的可能性是,在三次旋转中至少一次击中 12 个或 9 个数字,其概率等于 [1-(25/37)x(25/37)x(28/37)]=0.65451。因此,对于相同的资金和相同的回报,如果您投注更少的数字和更少的钱,但可能旋转更多次,您就可以像选项 (B) 那样提高成功的概率。(因为您可能在第一次旋转中获胜)如果您一次只投注六个数字并尝试赢得 250 美元,您甚至可以进一步提高您的概率。有什么解释吗?!!!!我向您致以最崇高的敬意,并期待您的回复。
您说得对,尽管目标和本金相同,但选项B的成功概率更大。原因是选项B的平均投注金额较小,因此您的资金承受的庄家优势较小,从而获胜的概率更高。选项A的投注金额始终为500美元。选项B的平均投注金额为(12/37)*125 + (25/37)*(12/37)*(125+187.5)+ (25/37)*(25/37)*(125+187.5+187.5) = 337.29。
当我参加拉斯维加斯挑战赛时,离比赛结束还有几分钟,我手头大约有8000美元,需要至少赢到24000美元。所以我把资金分成四堆,每堆2000美元,每堆都押注一个4个数字的组合,每个组合的赔率是22000美元。这样,我就不必把全部赌注都押在赌场优势上,从而增加了我赢钱的概率。
如果在轮盘赌上押注全部 38 个数字,那么即使在短时间内也不可能战胜赔率,如果每个数字押注 1 美元,那么每次转动轮盘就会损失 2 美元。(0、00 轮盘,没有对等额赌注的有利规则)根据统计数据确定一个最佳的赌注数字范围,这看起来合理吗?
我衡量投注价值的标准是预期回报,而不是中奖概率。因此,投注全部38个数字的庄家优势为2/38 = 5.26%,与投注单个数字或任意多个数字的庄家优势相同。虽然投注全部38个数字净赢的概率为0%,但缺点是只损失总投注金额的5.26%。如果被迫投注,并且希望最小化差异,那么您应该投注全部38个数字。举个实际的例子,如果您有促销筹码需要下注,而您不想冒险,那么就投注所有筹码以获得准确的预期价值。因此,回答您的问题,没有最佳的数字范围。所有范围的预期价值都相等。
今天有个故事,讲的是一位英国男子,他愿意把毕生积蓄都押在一次轮盘赌上。我和我的朋友一直在争论,对于这种类型的赌注,赌场里最好的选择是什么。如果你只能下注一次,并且希望最大化你的赔率,那么最好的游戏是什么?最好的选择又是什么?
首先,我要说这家伙是个傻瓜。他在一个普通的美式轮盘赌上押了13.8万美元,这个轮盘有两个零,赌场优势是5.26%。这相当于预期损失7263美元。然而,如果他坐10分钟的车去百乐宫、幻影酒店或阿拉丁酒店,他完全可以在单零轮盘赌上押注,因为单零轮盘遵循欧式规则,如果球落在零上,他会退还一半的等额投注。反正他打算押等额投注。所以,在这些完全遵循欧式规则的轮盘赌上,他的赌场优势只有1.35%,预期损失只有1865美元。
回答你的问题,如果被迫只进行一次等额赌注,我会选择百家乐中的庄家赌注,其赌场优势为 1.06%。
如果轮盘赌采用以下投注模式,我的破产风险有多大?
破产风险问题在数学上很复杂。除非是简单的输赢游戏,否则我建议在计算机上进行随机模拟。
我住在新泽西州,距离大西洋城以北约两小时车程。你知道离我家最近的欧洲轮盘赌在哪里吗?
大西洋城有很多单零轮盘。那里的大多数赌场都有,但最低投注额为25美元。
我当时在Casino On Net赌场玩轮盘赌。我押的是稳妥的注,只押在第一个12(大注)、第二个12(中注)和第三个12(高注)上。我转了5圈都没下注,等着某个组合的图案不出现,就押注,希望这能改变我中奖的概率。5圈之后,大注没出现。我继续押大注,我猜1、2、3、4、5、6、7、8、9、10、11或12会在12圈内出现,这样至少能赢回我的钱……但并没有。赌桌连续转了17圈,都没出现小注,我的奖金从258美元降到了0美元……反正都是奖金。这个问题分为三个部分:
- 我等待 5 次旋转而没有出现小数字是否真的增加了出现 L 的概率?
- 低数字连续 16 次不出现的概率是多少?
- 低数字连续 17 次不出现的概率是多少?
谢谢,我也想感谢你的那本《二十一点指南》,我用你的方法把 5.00 美元变成了 100.00 美元。
- 不
- Casino on Net 使用单零轮盘。因此,出现 16 次零的概率为 (25/37) 16 = 0.1887%。
- (25/37) 17 = 0.1275%。
庄家在轮盘赌 10 次旋转中得到 5 个相同数字的概率是多少?
在双零轮盘游戏中,任意数字在 10 次旋转中恰好出现 5 次的概率可以近似为 38* combin (10,5)*(1/38) 5 *(37/38) 5 = 1/359275。
恭喜你创建了一个很棒的网站。我完全理解你对21点赔率6比5的差距感到愤怒,但我也很好奇为什么美国人似乎毫无异议地接受了00轮盘赌。这种轮盘赌简直是犯罪,应该和基诺和老虎机并列。
谢谢。你说得对。通常情况下,6比5二十一点的庄家优势是1.44%,而双零轮盘赌的庄家优势是5.26%。这差了3.7倍。然而,这些年来我的经验告诉我,无论庄家优势有多差,让玩家放弃他们喜欢的游戏几乎是不可能的。所以我能做的最好的就是建议他们如何玩他们喜欢的游戏。对于二十一点玩家来说,3比2的游戏仍然不缺。玩6比5会让赌场毫无理由地多赢0.8%。我还强调,如果你是轮盘赌玩家,寻找单零轮盘赌非常重要。所以我认为这并没有什么矛盾。
能否请您解释一下轮盘赌的赌桌限额是如何运作的,以及单个号码的最低限额和赌桌限额之间有什么区别?如果可以的话,请举例说明。
轮盘赌通常有两个最低投注额。例如:外围投注 5 美元,内围投注 1 美元。外围投注包括所有等额投注、列注和十二注。内围投注则指投注数字,包括 2、3、4、5 和 6 的数字组合。在这种情况下,外围投注的最低投注额为 5 美元,内围投注的最低投注额为 1 美元。但是,内围投注的总投注额必须至少为 5 美元,否则不投注。
我在赌场工作,有人打赌说轮盘荷官无法影响掷骰结果。肯定有人认为可以。当然不是影响某个数字,而是影响轮盘的某个部分。你认为应该用什么测试来合理地判断荷官是否影响了结果?假设试验次数合理,我很乐意分享结果。
我支持你。如果真能做到这一点,那么荷官就能轻易地与玩家合谋,瓜分利润。但我从未听说过这种情况。一个很好的测试方法是找一个声称能够影响掷骰结果的人,让他在 100 次旋转中尽可能多地尝试将骰子投到轮盘的特定半边。他尝试的次数越多,他的说法就越有说服力。下表显示了 50 到 70 次旋转成功的概率。例如,60 次或更多次旋转成功的概率是 2.8444%。统计学中常见的置信阈值是 90%、95% 和 99%。要通过 90% 置信度测试(其中随机旋转失败的概率为 90%),成功旋转的次数需要达到 57 次或更多。要通过 95% 的测试,成功旋转的次数需要达到 59 次或更多,而要通过 99% 的测试,成功旋转的次数需要达到 63 次或更多。
至少 50 到 70 次轮盘赌成功旋转的概率
| 胜利 | 可能性 |
| 70 | 0.000039 |
| 69 | 0.000092 |
| 68 | 0.000204 |
| 67 | 0.000437 |
| 66 | 0.000895 |
| 65 | 0.001759 |
| 64 | 0.003319 |
| 63 | 0.006016 |
| 62 | 0.010489 |
| 61 | 0.0176 |
| 60 | 0.028444 |
| 59 | 0.044313 |
| 58 | 0.066605 |
| 57 | 0.096674 |
| 56 | 0.135627 |
| 55 | 0.184101 |
| 54 | 0.242059 |
| 53 | 0.30865 |
| 52 | 0.382177 |
| 51 | 0.460205 |
| 50 | 0.539795 |
www.ccc-casino.com 有无零轮盘,他们称之为超级机会轮盘。有没有其他系统可以有效应对没有零的情况?如果没有零,玩家可以同时有效地玩红黑轮盘吗?因为不用担心零。
我试图找到那个游戏,但当我查看时,网站已经瘫痪了。然而,假设这样的游戏确实存在,答案是否定的。从长远来看,没有任何系统能够击败它,也不会输给它。每个系统的预期值都恰好为零。
单0轮盘。任意一个数字(0-36)在连续三次旋转中出现多次的概率是多少?感谢您抽出时间!
无论第一个数字是多少,只有第二个旋转匹配它的概率是 (1/37)*(36/37)。只有第三个旋转匹配它的概率是 (36/37)*(1/37)。两个旋转都不匹配,但第二个和第三个旋转互相匹配的概率是 (36/37)*(1/37)。第二个和第三个旋转都匹配它的概率是 (1/37)*(1/37)。将所有这些加起来,您将得到 3*(1/37)*(36/37)+ (1/37)*(1/37) = 7.962%。
我想你可能会对此感兴趣。我在英国用的是Betfair。我敢肯定你们这些好心人在美国因为某些原因不能用它。如果你不熟悉它,可以去betfair.co.uk看看。它是一个博彩交易所,不是博彩公司。总之,我的问题是:他们现在提供无零轮盘,没错,就是无零轮盘。这确实是真的。你能想到一个好的策略吗?如果有的话,你会保密吗?祝好,乔纳森。附言:他们也提供其他没有庄家优势的赌场游戏。
我尝试在那里注册一个账户来查看情况,但他们屏蔽了美国玩家。我被告知最低投注额为2英镑,最高投注额为50英镑。即使是像无零轮盘这样的零庄家优势游戏,也没有任何投注系统能够超过或低于0%这个数字。无论你做什么,你投注的越多,实际庄家赢利就越接近0%。
你说轮盘赌没有必胜法。贡萨洛·加西亚-佩拉约和他的家人在世界各地的许多赌场赢了很多钱。他们甚至出版了一本书,描述了他们是如何做到的。你对此有何看法?
我曾经看过一个关于他的电视节目,我很欣赏他的做法。我所定义的“系统”是指一种投注模式,例如马丁格尔策略,应用于具有庄家优势的游戏,例如公平的轮盘赌。Gonzalo Garcia-Pelayo成功做到的是调查球落在每个数字上的概率,以便发现并利用存在偏差的轮盘赌机制。我称之为策略,而不是系统。有很多可以击败赌场的盈利策略,但却没有盈利的投注系统。
如果我向您展示一款没有零的轮盘游戏,并且所有常见的轮盘规则都适用,那么有可能 100% 获胜吗?
不。
我是你们时事通讯的长期订阅者,至今仍很喜欢你们的网站。我偶然发现一个赌场网站,它提供的轮盘赌没有零,只有1-36的数字,所有标准的轮盘赌规则都适用。你们有什么办法可以利用这一点吗?我知道你们不喜欢投注系统,但这个网站没有庄家优势。肯定有一个资金管理系统,可以在这些赌桌限额下盈利。任何建议都值得感激。
谢谢你的赞美。我想我之前回答过这个问题,但答案是否定的。即使没有赌场优势,从长远来看,仍然没有任何投注系统能够获胜。
您好,出于显而易见的原因,如果您不告诉任何人我的名字,我将不胜感激。在我工作的赌场,轮盘荷官几乎一致认为,他们可以“控制旋转”,轻松击中轮盘的某些部分,或者故意错过其他部分。考虑到轮盘中球旋转的所有因素,包括球侧面的凸起(凸起)、球的方向和轮盘的速度等等——您觉得这有什么意义吗?一个不诚实的荷官就能帮助玩家克服巨大的赌场优势吗?
这远非我第一次听到这种说法,我对此深表怀疑。大多数荷官也相信一些流言蜚语,比如糟糕的三垒手会导致其他玩家在二十一点游戏中输钱,所以总的来说,他们并不是最怀疑的一群人。我认为真正的原因是,他们记得自己成功控制旋转的次数,却轻易忘记了失败的次数。就像他们记得三垒手抢走荷官爆牌的次数,却忘记了他拯救牌桌的次数一样。
如果荷官真能做到这一点,那么很容易就能找到同伙,让他赢,让其他玩家输,以此来弥补损失。只要他们按照正确的程序进行旋转,并且不与同伙一起出现在公共场合,这一切看起来就完全合法。然而,你从未听说过这种事。我想那些相信的人可能会说,这样做的人只是在保持低调,但那些相信毫无价值的投注系统的人也会这么说。如果这真的像你工作的轮盘赌荷官说的那么容易,那么由此产生的作弊问题就会非常猖獗。
在双零轮盘赌中,第 200 次旋转时任何数字都不会出现的概率是多少?
任何给定数字不会命中的概率是 (37/38) 200 = 0.48%。
对于 38 个数字,我们可能会错误地说其中任何一个数字都不会被击中的概率是 38 × (37/38) 200 = 18.34%。
这是不正确的,因为它重复计算了两个未中数字的概率。所以我们需要减去这些概率。38 个数字中,有(38,2) = 703 组,每组 2 个。任意两个给定数字未中概率为 (36/38) 200 = 0.000020127。我们需要减去避开这两个数字的概率。因此,我们得到:
38×(37/38) 200 - 组合(38,2)×(36/38) 200 = 16.9255%。
然而,现在我们已经抵消了三个号码未中奖的概率。对于任何给定的三个号码组,我们将任意一个号码未中奖的概率计算三次。然后,我们分别减去三次,从三个号码中选出两个号码,最后三个号码全部未中奖的概率为零。共有 combin(38,3)=8,436 个这样的组。将它们加回去,我们现在得到:
38×(37/38) 200 - 组合(38,2)×(36/38) 200 + 组合(38,3)×(35/38) 200 = 16.9862%。
然而,现在我们高估了四个号码未中奖的概率。对于 combin(38,4)=73,815 组四个号码中的每一组,最初都计算了四次。然后,我们减去了 combin(4,2)=6 组(每组 2 个号码)中的每一组。之后,我们又加回了 4 组(每组 3 个号码)中的 3 个号码。因此,对于每个四个号码的并集,它被计算了 4 − 6 + 4 = 2 次。为了调整重复计算,我们必须对每一组进行减法。减去这些数字后,我们现在得到:
38×(37/38) 200 - 组合(38,2)×(36/38) 200 + 组合(38,3)×(35/38) 200 - 组合(38,4)×(34/38) 200 = 16.9845%。
继续这个过程,我们会不断交替进行加减运算,直到丢失37个数字。因此,至少一个数字永远不被选中的概率是:
总和 i=1 至 37 [(-1) (i+1) × combin(38,i) × ((38-i)/38) 38 ] = 16.9845715651245%
以下是对 126,900,000 个这样的 200 次旋转实验进行随机模拟的结果。
200 次轮盘赌中命中的数字
| 数字命中 | 观察 | 比率 |
|---|---|---|
| 31岁或以下 | 0 | 0 |
| 三十二 | 1 | 0.00000001 |
| 33 | 33 | 0.00000026 |
| 三十四 | 1812 | 0.00001428 |
| 三十五 | 68845 | 0.00054251 |
| 三十六 | 1577029 | 0.01242734 |
| 三十七 | 19904109 | 0.15684877 |
| 三十八 | 105348171 | 0.83016683 |
| 全部的 | 126900000 | 1 |
至少一个数字未被击中的次数比率为 0.169833。
我有个朋友是赌场工作人员,负责看管轮盘赌桌。他告诉我,每当有人开始赢钱,赌场就会换荷官。我还见过工作人员要求荷官以不同的速度旋转轮盘。这难道不意味着赌场确信荷官能够让一系列非随机的数字出现吗?这难道不意味着赌徒可以去寻找“幸运”赌桌,荷官的旋转速度越快,他们赢钱的几率就越大吗?
可悲的是,无知的程度甚至会上升到相当高的程度。我并不否认专家可以计算出轮盘旋转速度有多慢。然而,撇开这个问题不谈,更换荷官并不能改变赔率。没有幸运或不幸的荷官之说。迷信很难戒除。正如我多次说过的,一种信念越荒谬,就越容易被人们固执地坚持下去。
先生,我玩了8672场自动单零轮盘游戏。我预设的号码竟然出现了278次。我选择这个号码是因为口袋的磨损。我怎么确定这个号码的概率高于1/37呢?
如果我的术语正确的话,“预测轮盘”是指根据球速、球位置和轮盘速度来预测球的落点。听起来你的做法是在利用偏向性轮盘,这是一种不同的优势玩法。既然我们讨论的是这个话题,那么第三种优势玩法就是利用“荷官签名”,荷官的玩法非常稳定,以至于每次旋转球和轮盘的速度几乎都相同。这使得玩家能够根据球的位置和过往结果来预测球的落点。
回答你的问题,你预期中奖的次数是 8672/37=234.38。方差是 8672×(1/37)×(36/37)=228.04。标准差是方差的平方根,即 15.10。你的中奖次数比预期多了 278-234.38=43.62。也就是 (43.62-0.5)/15.10 = 2.8556 个标准差。减去 0.5 的原因很难解释。简而言之,这是一个使用连续函数估计离散函数的调整因子。进行高斯近似,中奖次数达到或超过这个数字的概率是 0.21%。所以,你很有可能遇到了一个有偏差的轮盘。然而,仍有 1/466 的可能性,这只是运气好而已。
20年前,日本豪赌客柏木与唐纳德·特朗普之间发生了一场著名的淘汰赛。柏木在百家乐中每手的投注不得超过20万美元。当赌场或玩家领先1200万美元时,游戏就会结束。假设柏木总是在庄家上押最大注,那么柏木获胜的概率是多少?
如果他押注闲家,计算起来就容易多了。我在我的 mathproblems.info 网站上算过一个类似的轮盘赌题,题号 116。对于等额投注,通用公式是 ((q/p) b -1)/((q/p) g -1),其中:
b = 起始资金(以单位计)。
g = 资金目标(以单位计)。
p = 赢得任何给定赌注的概率,不包括平局。
q = 在任何给定赌注中失败的概率,不包括平局。
此处,玩家初始资金为1200万美元,即60个单位,每个单位20万美元,并将一直玩到资金达到120个单位或破产。因此,在玩家下注的情况下,等式值为:
b = 60
克= 120
p = 0.493175
q = 0.506825
所以答案是 ((0.506825/0.493175) 60 -1)/(( 0.506825/0.493175) 120 -1) = 16.27%。
由于庄家投注有5%的佣金,情况要复杂得多。这会导致玩家超额完成目标的可能性很大。如果我们增加一条规则:如果赢钱的赌注能够帮助玩家实现目标,那么他只需下注达到1200万美元所需的金额,那么我估计他成功的概率为21.66%。
资金翻倍概率的一个更简单的公式是 1/[1+(q/p) b]。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
平均而言,在 38 个数字的轮盘赌中,需要进行多少次试验才会重复出现任何数字?
计算第一次试验,我显示平均值为 8.408797,中位数为 8,众数为 7。
两个数字不重复的概率是 37/38 = 97.37%。
三个数字不重复的概率是(37/38)×(36/38)= 92.24%。
四个无重复数字的概率为 (37/38)×(36/38)×(35/38) = 84.96%。
按照这种模式,8 个数字中没有重复的概率是 (37/38)×(36/38)×(35/38)×...×(31/38) = 45.35%。
因此,8 个数字内重复的概率为 100% - 45.35% = 54.65%。
我猜大多数人会认为8个数字以内重复的概率会低于这个数字。如果你不介意占你数学不好的朋友的便宜,可以跟他们打赌,至少有一个数字重复的概率是8个或更少。这样你就押8个或更少,你的朋友押9个或更多。如果他/她犹豫不决,那就押7个或以上,这样赢的概率是55.59%。基本上,任何一方的中位数是8的一方都有可能赢。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
探索频道的《Hustling the House》节目中有一长段节目,探讨如何将30美元变成1000美元。节目中,安迪·布洛赫说道:“如果你口袋里有30美元,你想把它变成1000美元,那么轮盘赌是你唯一的选择。” 安迪接着解释了为什么把全部30美元押在一个数字上比五次等额投注更好。
安迪说得对,将 30 美元变成 1,000 美元的最佳方式是将全部 30 美元押在轮盘赌中的一个数字上,对吗?
不,他错了。安迪的单注策略的概率是1/38 = 2.6316%。
经过多次反复试验,我设计出了“万福玛利亚”轮盘赌策略,该策略将 30 美元变成 1,000 美元的几率提高到 2.8074%。
巫师的轮盘赌“万福玛利亚”策略:
此策略假设投注必须以 1 美元为增量。所有投注计算均向下取整。
让:
b = 您的资金
g = 你的目标
- 如果 2*b >=g,则在任何等额赌注上投注 (gb)。
- 否则,如果 3*b >=g,则在任意列上投注 (gb)/2。
- 否则,如果 6*b >=g,则在任意六行(六个数字)上投注 (gb)/5。
- 否则,如果 9*b >=g,则在任意角(四个数字)下注 (gb)/8。
- 否则,如果 12*b >=g,则在任意街道(三个数字)上投注 (gb)/11。
- 否则,如果 18*b >=g,则在任何分割(两个数字)上投注 (gb)/17。
- 否则,对任意单个数字下注 (gb)/35。
换句话说,尽量只用一次投注就达到目标,但不要超过目标金额。如果有多种方法可以实现目标,那就选择获胜概率最大的那个。
你可能会问,其他游戏怎么样?探索频道的配音员说:“大家都同意轮盘赌是赌场里最好的快速致富计划。” 好吧,我不这么认为。即使只限于常见的游戏和规则,我也觉得掷骰子更好。尤其是在押注不及格和下注赔率方面。
按照我的掷骰子“万福玛利亚”策略(下文会解释),30 美元变成 1,000 美元的概率是 2.9244%。这假设玩家可以下注 6 倍赔率,无论点数是多少(即允许 3 倍、4 倍或 5 倍赔率下注的情况)。这个成功概率比我的轮盘赌“万福玛利亚”策略高 0.117%,比安迪·布洛赫策略高 0.2928%。
安迪可能会辩称,我上述论点依赖于最低下注额为 1 美元的假设,这在拉斯维加斯的真人荷官游戏中很难实现。考虑到有人会这么说,我把最低下注额设为 5 美元,并以 5 美元为增量进行下注,并以此为前提,玩了两局游戏。在这种情况下,使用我的“万福玛利亚”策略,在轮盘赌中获胜的概率为 2.753%,在掷骰子中获胜的概率为 2.891%。这两种情况下,都高于安迪·布洛赫策略下的 2.632%。
平心而论,探索频道绝不会把上面那段疯狂的咆哮搬上电视,他们肯定想找一些大众能理解的简单易懂的内容。安迪肯定在给他们讲他们想听的东西。他建议的基本前提是,如果你想达到某个目标,那么“打了就跑”的策略比让赌场优势把你压垮在多重赌注下要好得多。这绝对是真的,也是我17年来一直在宣扬的理念。
巫师的掷骰子“万福玛利亚”策略。
此策略假设投注必须以 1 美元为增量,且赢取的金额将向下取整至最接近的美元。计算投注时,切勿下注过多,以免超出目标金额。此外,切勿下注超过四舍五入金额。
让:
b = 您的资金
g = 你的目标
- 在不通过的情况下下注 max($1,min(b/7,(gb)/6))。
- 如果掷出一个点,并且你的筹码足够进行全额赔率投注,那么就押全额赔率。否则,尽可能押注。
所以,我希望安迪和探索频道能够开心。我花了好几天时间进行模拟,就是为了证明他们错了。
这个问题是在我的“拉斯维加斯巫师”论坛上提出并讨论的。
轮盘赌中,第 4、5、6、7、8 或 9 次旋转内球落在 1、2 和 3 的概率是多少?
一般公式为:
Pr(球落在 1) + Pr(球落在 2) + Pr(球落在 3) - Pr(球落在 1 和 2) - Pr(球落在 1 和 3) - Pr(球落在 2 和 3) + Pr(球落在 1、2 和 3)。
在双零轮盘赌中,对于 n 次旋转,结果为 3*(1-(37/38)^n)-3*(1-(36/38)^n)+(1-(35/38)^n)。
下表显示了单零和双零轮盘赌中从 3 到 100 次旋转中滚动出所有三个数字的概率。
轮盘赌问题
| 旋转 | 单身的 零 | 双倍的 零 |
|---|---|---|
| 3 | 0.000118 | 0.000109 |
| 4 | 0.000455 | 0.000420 |
| 5 | 0.001091 | 0.001009 |
| 6 | 0.002094 | 0.001939 |
| 7 | 0.003518 | 0.003261 |
| 8 | 0.005404 | 0.005016 |
| 9 | 0.007785 | 0.007234 |
| 10 | 0.010684 | 0.009937 |
| 15 | 0.033231 | 0.031066 |
| 20 | 0.068639 | 0.064476 |
| 二十五 | 0.114718 | 0.108254 |
| 三十 | 0.168563 | 0.159750 |
| 三十五 | 0.227272 | 0.216265 |
| 40 | 0.288292 | 0.275379 |
| 45 | 0.349548 | 0.335089 |
| 50 | 0.409453 | 0.393835 |
| 55 | 0.466865 | 0.450467 |
| 60 | 0.521017 | 0.504191 |
| 65 | 0.571445 | 0.554501 |
| 70 | 0.617922 | 0.601122 |
| 75 | 0.660393 | 0.643951 |
| 80 | 0.698930 | 0.683016 |
| 85 | 0.733693 | 0.718435 |
| 90 | 0.764897 | 0.750386 |
| 95 | 0.792791 | 0.779086 |
| 100 | 0.817638 | 0.804773 |
在墨西哥的某些赌场,轮盘赌用骰子代替轮盘。规则如下:
- 有四个骰子——两个绿色,一个红色,一个蓝色。
- 如果两个绿色骰子都落在一个点上,则“旋转”的结果为零。
- 如果两个绿色骰子都落在六上,那么“旋转”的结果将是双零。
- 如果绿色骰子出现任何其他结果,则红色和蓝色骰子的 36 种可能结果应映射到数字 1 和 36 以表示“旋转”。
与传统轮盘赌相比,这会如何改变赔率?
0和00的中奖概率分别为1/36。如果投注这些结果的赔率是通常的35比1,那么赌场优势就恰好是0%。
其他任何数字的中奖概率为 (34/36)*(1/36) = 2.62%。相比之下,传统双零轮盘的中奖概率为 1/38=2.63%。投注 1 至 36 的庄家优势为 5.56%。相比之下,传统双零轮盘的庄家优势为 5.26%。我建议在这款游戏中只投注零和双零。
如果有人可以确认或否认这些规则和报酬,请告诉我。
我记录了7456次轮盘赌的旋转。结果如下。我怀疑轮盘有偏差,但不确定数据是否足够确凿,可以玩这个游戏。
轮盘数据
| 获胜 数字 | 发生 |
|---|---|
| 0 | 204 |
| 二十八 | 214 |
| 9 | 175 |
| 二十六 | 177 |
| 三十 | 203 |
| 11 | 181 |
| 7 | 223 |
| 20 | 205 |
| 三十二 | 184 |
| 17 | 222 |
| 5 | 224 |
| 22 | 241 |
| 三十四 | 194 |
| 15 | 210 |
| 3 | 209 |
| 24 | 176 |
| 三十六 | 203 |
| 十三 | 217 |
| 1 | 217 |
| 00 | 197 |
| 二十七 | 173 |
| 10 | 195 |
| 二十五 | 198 |
| 二十九 | 217 |
| 12 | 197 |
| 8 | 207 |
| 19 | 163 |
| 31 | 180 |
| 18 | 201 |
| 6 | 186 |
| 21 | 203 |
| 33 | 171 |
| 16 | 164 |
| 4 | 200 |
| 23 | 191 |
| 三十五 | 163 |
| 14 | 177 |
| 2 | 194 |
| 全部的 | 7456 |
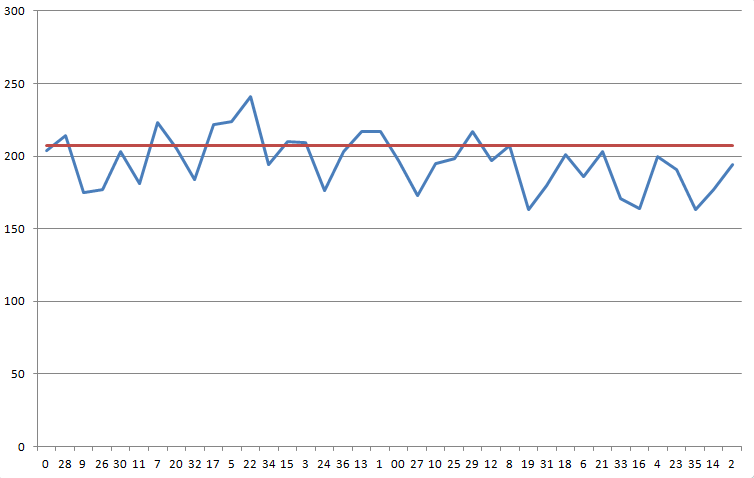
下图按顺序显示了您在轮盘上的结果。蓝线表示您的结果。红线表示您需要的数字 207.11,以克服 5.26% 的赌场优势。
对该分布进行卡方检验,结果显示自由度为 37,统计量为 68.1。出现这种或以上偏态分布的概率为 1/725。
我认为卡方检验并非适用于这种情况的最佳方法,因为它没有考虑结果的顺序,但我也不知道有更好的检验方法。有人建议使用Kolmogorov-Smirnov 检验,但我认为这并不合适。如果有其他合适的检验方法,我洗耳恭听。
我可以说,如果你押注围绕数字5的3个数字弧,那么你记录的旋转次数将获得10.57%的利润。然而,如果你押注围绕数字5的7个数字弧,利润率就会下降到2.84%。
如果非要用通俗易懂的语言来回答,我会说轮盘确实存在偏见,但并非确凿无疑的证据。然而,这种偏见可能不足以显著且自信地克服赌场优势。假设赌场不在赌桌之间调换轮盘,我认为在下大注之前应该收集更多数据。很抱歉,我的回答如此模棱两可。
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
在单零轮盘赌中,每个数字至少出现一次所需的平均旋转次数和中位数是多少?
求平均值要容易得多,所以我们就从平均值开始。让我们一步一步来:
- 第一次旋转肯定会出现一个新数字。
- 第二次旋转出现新数字的概率为 36/37。如果某个事件的概率为 p,则该事件发生的预期尝试次数为 1/p。在这种情况下,出现第二个数字的预期尝试次数为 37/36 = 1.0278。
- 观测到两个数字后,下次旋转出现新数字的概率为35/37。因此,观测到第二个数字后,预期旋转次数为37/35 = 1.0571。
- 按照这个逻辑,看到每个数字的平均旋转次数是 1 + 37/36 + 37/35 + 37/34 + ... + 37/2 + 37/1 = 155.458690。
中位数要复杂得多。为了找到确切的答案,与使用随机模拟不同,我们需要运用大量的矩阵代数运算。我已经在其他“问巫师”问题中讨论过如何解决类似的问题,因此不再赘述。类似问题的一个例子是连续三次掷出一对 6-6 的概率,正如“问巫师”#311中讨论的那样。可以说,在 145 次旋转中看到所有数字的概率是 0.49161779,在 146 次旋转中看到所有数字的概率是 0.501522154。因此,中位数是 146。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
如果⼀颗球在上20局都落在红⾊上⾯, 它下⼀局落在⿊⾊上⾯的机率为何?
和红⾊⼀样, 47.37%在两个零的轮盘上, 18个⿊⾊号码除以38个号码总数。
我认为你在上个问题答错了。连续出现21次红⾊的概率是 (18/38)^21 = 1 in 6,527,290. 概率必然远远偏向⿊⾊这边。
那是真的, 但是⽆所谓。连续20次红⾊之后出现⿊⾊的机率也是这般相同的。事实上是, 像轮盘这般的赌戏, 过去的事件并不影响赌局的独⽴性。
我想到击败赌场轮盘的⼀种⽅法!开始下注在任何even-money等额赔率的押注上⾯, 像是红⾊或⿊⾊, 如果输了, 就在同个地⽅加倍赌注, 就这样持续加倍直到赢为⽌。赢的结果最终还是会发⽣, 当最后赢的时候, 我将会获得原来的赌注⾦额。依此反覆施为。你的意⻅为何? 还有, 请不要告诉任何⼈。
这可能是押注妙⽅当中最流⾏的, 称之为「Martingale加倍赌注」。从古⽼年代以来赌徒们就被它所蒙骗。就像所有的押注妙⽅那般, 这不仅不能击败赌场优势, 它甚⾄影响不了什么。赌徒最后会惨输的原因是因为他的资⾦再也负担不起另⼀次的加倍赌注。
在之前的回答, 你解释了为什么「Martingale加倍赌注」⽆法运作的原因。那么反过来呢?每次赢注之后再加倍赌注、直到达标为⽌?
这个称为「anti-Martingale反加倍赌注」也是⼀样⽆⽤。随着你的资本愈来愈少、更加不可能让你达标。⽆论你使⽤哪种押注妙⽅、或者什么妙⽅也不⽤, 你玩得愈多, 在两个零的轮盘赌戏中, 你输掉的钱与押注的钱的⽐率将趋近于5.26%.
轮盘赌需要旋转多少次才能连续出现五个红色或五个黑色?
[/spoiler] 答案是 3872789/118098 =~ 32.79301089 次旋转。[/剧透]
这是我的解决方案(PDF)。
轮盘赌中的“三分法则”是什么?
“三分法则”指出,如果轮盘上的每个数字都旋转一次,则大约有 1/3 的数字永远不会出现。
1/3 确实是一个相当糟糕的估计。更好的估计应该是 1/e =~ 36.79%。双零轮盘赌的真实百分比是 36.30%。
下表显示了在 38 次双零轮盘旋转中观察到 1 到 38 个不同数字的概率。
三分法则——双零轮盘赌
| 清楚的 数字 | 可能性 |
|---|---|
| 1 | 0.000000000 |
| 2 | 0.000000000 |
| 3 | 0.000000000 |
| 4 | 0.000000000 |
| 5 | 0.000000000 |
| 6 | 0.000000000 |
| 7 | 0.000000000 |
| 8 | 0.000000000 |
| 9 | 0.000000000 |
| 10 | 0.000000000 |
| 11 | 0.000000000 |
| 12 | 0.000000000 |
| 十三 | 0.000000005 |
| 14 | 0.000000124 |
| 15 | 0.000001991 |
| 16 | 0.000022848 |
| 17 | 0.000191281 |
| 18 | 0.001186530 |
| 19 | 0.005519547 |
| 20 | 0.019434593 |
| 21 | 0.052152293 |
| 22 | 0.107159339 |
| 23 | 0.169042497 |
| 24 | 0.204864337 |
| 二十五 | 0.190490321 |
| 二十六 | 0.135436876 |
| 二十七 | 0.073211471 |
| 二十八 | 0.029838199 |
| 二十九 | 0.009063960 |
| 三十 | 0.002020713 |
| 31 | 0.000323888 |
| 三十二 | 0.000036309 |
| 33 | 0.000002742 |
| 三十四 | 0.000000132 |
| 三十五 | 0.000000004 |
| 三十六 | 0.000000000 |
| 三十七 | 0.000000000 |
| 三十八 | 0.000000000 |
| 全部的 | 1.000000000 |
表格显示,最有可能的结果是 24 个不同的数字,概率为 20.49%。平均值为 24.20656478。
有些江湖骗子会说,玩家应该观察前九个不同的结果,然后押注,因为他们错误地认为这些结果比其他数字更有可能出现。这完全是错误的!轮盘和球没有记忆。在一个公平的轮盘上,每个数字都有同等的可能性,过去的数字并不重要。