在这一页
如何计算每次投注的赌场优势
简介
介绍
欢迎来到掷骰子附录。在这里,我将推导掷骰子所有主要投注方式的玩家优势。在本附录之外,我通常会讨论庄家优势,它只是玩家优势乘以-1。为了避免每次投注都乘以-1,我将以玩家优势的形式讨论所有内容,玩家优势可以预期为负,因为除了免费赔率之外,所有投注方式最终都由庄家拥有优势。请稍等片刻,自己计算一下这些投注方式。这不仅能让你更深入地理解赔率,还能激励你更新或提高你的数学技能。
在继续阅读之前,你必须了解一次掷出每个点数的概率。我的骰子概率基础页面对此进行了深入解释。如果你不知道或无法弄清楚掷出 6 的概率是 5/36,那么访问该页面是阅读本页面的先决条件。
投注预期回报的一般公式是:
∑(事件 i 的概率)×(事件 i 的回报)涵盖所有可能的结果。
玩家优势等于预期回报除以初始投注。例如,在体育赛事中做反向投注时,你必须下注11美元才能赢得10美元。假设获胜概率为50%,预期回报为0.5×(10) + 0.5×(-11) = -0.5。玩家优势为-0.5/11 = -1/22 ≈ -4.545%。
赌场优势规则的一个例外是平局可能出现的情况。通常,赌场优势计算时会忽略平局。为了进行调整,当可能出现平局时,将预期回报除以已解决的平均投注额。“已解决的平均投注额”是初始投注额与该投注被解决的概率的乘积。在掷骰子游戏中,唯一会出现平局的投注是“不过线”和“不来”。
掷骰子游戏中,如果一个特定事件先于另一个事件发生,很多赌注都会赢。这些赌注可能需要多次甚至更多次才能解决。如果一个赌注赢的概率为 p,输的概率为 q,并且持续有效的概率为 1-pq,那么最终赢的概率为:
∑ p×(1-pq) i (i=0 至无穷大)=
p × (1/(1-(1-pq))) = p × (1/(p+q)) = p/(p+q)。
在本页中,你会看到很多 p/(p+q) 形式的表达式。为了节省篇幅,我不再每次都推导这个表达式,因为它上面已经算出来了。
传球/来球
掷出点数获胜的概率为 pr(7)+pr(11) = 6/36 + 2/36 = 8/36。
建立点数然后获胜的概率是 pr(4)×pr(7 之前 4) + pr(5)×pr(7 之前 5) + pr(6)×pr(7 之前 6) + pr(8)×pr(7 之前 8) + pr(9)×pr(7 之前 9) + pr(10)×pr(7 之前 10) =
(3/36)×(3/9)+(4/36)×(4/10)+(5/36)×(5/11)+(5/36)×(5/11)+(4/36)×(4/10)+(3/36)×(3/9)=
(2/36)×(9/9 + 16/10 + 25/11)=
(2/36)×(990/990 + 1584/990 + 2250/990)=
(2/36)×(4824/990)= 9648/35640
总体获胜概率为 8/36 + 9648/35640 = 17568/35640 = 244/495
输的概率显然是1-(244/495) = 251/495
因此,玩家的优势为 (244/495)×(+1) + (251/495)×(-1) = -7/495 ≈ -1.414%。
不通过/不来
掷出结果获胜的概率是 pr(2)+pr(3) = 1/36 + 2/36 = 3/36。
掷出结果时平局的概率为 pr(12) = 1/36。
建立点数并获胜的概率为 pr(4)×pr(4 之前 7) + pr(5)×pr(5 之前 7) + pr(6)×pr(6 之前 7) + pr(8)×pr(8 之前 7) + pr(9)×pr(9 之前 7) + pr(10)×pr(10 之前 7) =
(3/36)×(6/9)+(4/36)×(6/10)+(5/36)×(6/11)+(5/36)×(6/11)+(4/36)×(6/10)+(3/36)×(6/9)=
(2/36)×(18/9 + 24/10 + 30/11)=
(2/36)×(1980/990 + 2376/990 + 2700/990)=
(2/36)×(7056/990)= 14112/35640
总获胜概率为 3/36 + 14112/35640 = 17082/35640 = 2847/5940
输的概率是 1-(2847/5940 + 1/36) = 1-(3012/5940) = 2928/5940
预期收益为 2847/5940×(+1) + 2928/5940×(-1) = -81/5940 = -3/220 ≈ 1.364%
大多数其他关于掷骰子的资料都声称,不及格投注的赌场优势是 1.403%。造成这种差异的原因在于是否计算平局。我倾向于将平局算作金钱投注,而其他人则不这么认为。我不是在说哪一方是对是错,只是我更喜欢计算平局。如果您不将平局算作金钱投注,则应将上述数字除以投注结果为赢或输的概率 (35/36)。因此,1.364%/(35/36) ≈ -1.403%。这是假设玩家在开局掷骰中从未掷出 12 点的情况下的赌场优势。
下注赢钱
押注 6 或 8:[(5/11)×7 + (6/11)×(-6)]/6 = (-1/11)/6 = -1/66 ≈ -1.515%
押注 5 或 9:[(4/10)×7 + (6/10)×(-5)]/5 = (-2/10)/5 = -1/25 = -4.000%
押注 4 或 10:[(3/9)×9 + (6/9)×(-5)]/5 = (-3/9)/5 = -1/15 ≈ -6.667%
下注输
押注 6 或 8 输:[(6/11)×4 + (5/11)×(-5)]/5 = (-1/11)/5 = -1/55 ≈ -1.818%
押注 5 或 9 输:[(6/10)×5 + (4/10)×(-8)]/8 = (-2/10)/8 = -1/40 = -2.500%
押注 4 或 10 输:[(6/9)×5 + (3/9)×(-11)]/11 = (-3/9)/11 = -1/33 ≈ -3.030%
注意:实体赌场不允许此类投注。只有部分网络赌场允许此类投注。
买
买入押注 6 或 8:[(5/11)×23 + (6/11)×(-21)]/21 = (-11/11)/21 = -1/21 ≈ -4.762%
买入押注 5 或 9:[(4/10)×29 + (6/10)×(-21)]/21 = (-10/10)/21 = -1/21 = -4.762%
买入押注 4 或 10:[(3/9)×39 + (6/9)×(-21)]/21 = (-9/9)/21 = -1/21 ≈ -4.762%
莱伊
押注 6 或 8 输:[(6/11)×19 + (5/11)×(-25)]/25 = (-11/11)/25 = -1/25 ≈ -4.000%
押注 5 或 9 输:[(6/10)×19 + (4/10)×(-31)]/31 = (-10/10)/31 = -1/31 = -3.226%
押注 4 或 10 输:[(6/9)×19 + (3/9)×(-41)]/41 = (-9/9)/41 = -1/41 ≈ -2.439%
六大/八大
[(5/11)×1 + (6/11)×(-1)]/1 = -1/11 ≈ 9.091%
硬4/硬10
注意:硬 4 和硬 10 的赔率为 7比1,或 8比1。在掷骰子游戏中,布上的赔率以 1 为基础列出,包括上面的图表。
任何给定掷骰子时出现硬 4 的概率为 1/36。
任何给定掷骰子出现 7 的概率是 6/36。
任何给定掷骰子时出现软 4 的概率为 2/36(1+3 和 3+1)。
任何一次掷骰子获胜的概率都是 1/36。
任何一次掷骰子失败的概率是 6/36 + 2/36 = 8/36。
赢得赌注的概率是 p/(p+q)(见上文)= (1/36)/(9/36) = 1/9
预期回报率为 (1/9)×7 + (8/9)×(-1) = -1/9 ≈ 11.111%。
由于赌注为 1 个单位,因此玩家的优势也是 -1/9。
对于硬 10,赔率是相同的。
硬6/硬8
注意:硬 4 和硬 10 的赔率为 9比1,或 10比1。在掷骰子游戏中,布上的赔率以 1 为基础列出,包括上面的图表。
任何一次掷骰子出现硬 6 的概率都是 1/36。
任何给定掷骰子出现 7 的概率是 6/36。
任何给定掷骰子时出现软 6 的概率为 4/36(1+5、2+3、3+2 和 5+1)。
任何一次掷骰子获胜的概率都是 1/36。
任何一次掷骰子失败的概率是 6/36 + 4/36 = 10/36。
赢得赌注的概率是 p/(p+q)(见上文)= (1/36)/(11/36) = 1/11
预期回报率为 (1/11)×9 + (10/11)×(-1) = -1/11 ≈ 9.091%。
由于赌注为 1 个单位,因此玩家的优势也是 -1/11。
对于硬 8,赔率是相同的。
掷骰子 2/掷骰子 12
[(1/36)×30 + (35/36)×(-1)]/1 = -5/36 ≈ -13.889%
掷骰子 3/掷骰子 11
[(2/36)×15 + (34/36)×(-1)]/1 = -4/36 ≈ -11.111%
任何掷骰子
[(4/36)×7 + (32/36)×(-1)]/1 = -4/36 ≈ -11.111%
任意 7
[(6/36)×4 + (30/36)×(-1)]/1 = -6/36 ≈ -16.667%
喇叭
掷出 2 或 12 的概率是 1/36 + 1/36 = 2/36。
掷出 3 或 11 的概率是 2/36 + 2/36 = 4/36。
掷出其他点数的概率为 1-2/36-4/36 = 30/36。
记住,角注就像四种骰子赌注合而为一。即使其中一个赢了,其他三个仍然输。赌场优势如下:
[(2/36)×27 + (4/36)×12 + (30/36)×(-4)]/4 = (-18/36)/4 = 12.500%
场地
当 12 支付 2:1 时,预期回报为:
2×(pr(2)+pr(12)) + 1×(pr(3)+pr(4)+pr(5)+pr(10)+pr(11)) + -1×(pr(6)+pr(7)+pr(8)+pr(9)) =
2×(1/36 + 1/36) + 1×(2/36 + 3/36 + 4/36 + 3/36 + 2/36) + -1×(5/36 + 6/36 + 5/36 + 4/36) =
2×(2/36) + 1×(14/36) + -1×(20/36) = -2/36 = -1/18 ≈ 5.556%。
当 12 支付 3:1 时,预期回报为:
3×pr(2) + 2×pr(12)) + 1×(pr(3)+pr(4)+pr(5)+pr(10)+pr(11)) + -1×(pr(6)+pr(7)+pr(8)+pr(9)) =
3×(1/36) + 2×(1/36) + 1×(2/36 + 3/36 + 4/36 + 3/36 + 2/36) + -1×(5/36 + 6/36 + 5/36 + 4/36) =
3×(1/36) + 2×(1/36) + 1×(14/36) + -1×(20/36) = -1/36 ≈ 2.778%。
购买赔率
4 和 10:[(3/9)×2 + (6/9)×(-1)]/1 = 0.000%
5 和 9:[(4/10)×3 + (6/10)×(-2)]/2 = 0.000%
6 和 8:[(5/11)×6 + (6/11)×(-5)]/5 = 0.000%
赔率
4 和 10:[(6/9)×1 + (3/9)×(-2)]/1 = 0.000%
5 和 9:[(6/10)×2 + (4/10)×(-3)]/2 = 0.000%
6 和 8:[(6/11)×5 + (5/11)×(-6)]/5 = 0.000%
综合通行证和购买赔率
通过赔率和买入赔率组合的玩家优势等于玩家平均收益除以玩家平均投注。通过线的收益始终为 -7/495,而赔率的收益始终为 0。预期投注额取决于您允许的赔率倍数。假设全双倍赔率,即通过线投注为 2 美元,4、5、9 和 10 的赔率投注为 4 美元,6 或 8 的赔率投注为 5 美元。
平均增益为-2×(7/495) = -14/495。
平均投注额为 2 + (3/36)×4 + (4/36)×4 + (5/36)×5 + (5/36)×5 + (4/36)×4 + (3/36)×4] =
2 + 106/36 = 178/36
玩家优势为 (-14/495)/(178/36) = -0.572%。
如果 6 和 8 的赔率乘以 x,5 和 9 的赔率乘以 y,4 和 10 的赔率乘以 z,则一般公式为 (-7 / 495) / [ 1 + ((5x + 4y + 3z) / 18) ]
不通过赔率和下注赔率的组合
玩家在不及格赔率和下注赔率组合中的赢利等于玩家平均赢利除以玩家平均投注。不及格赔率的赢利始终为-3/220,而赔率的赢利始终为0。预期投注额取决于您允许的赔率倍数。假设赔率翻倍,不及格投注额为10美元。那么玩家可以投注40美元,在4和10上赢得20美元;投注30美元,在5和9上赢得20美元;投注24美元,在6和8上赢得20美元。平均赢利为-10×(3/220) = -30/220。
平均赌注为 10 + 2×[(3/36)×40 + (4/36)×30 + (5/36)×24] = 30。
玩家优势为 (-30/220)/30 = -0.455%。
一般公式是,如果您可以购买 x 倍赔率,那么组合不通过和下注赔率的庄家优势是 (3/220)/(1+x)。
每场净收益/损失
下表显示了100次尝试或最终掷出结果(come out rolls)后预期的净盈亏。为了方便绘制图表,假设玩家在过线(pass line)上投注1美元,并接受双倍赔率。
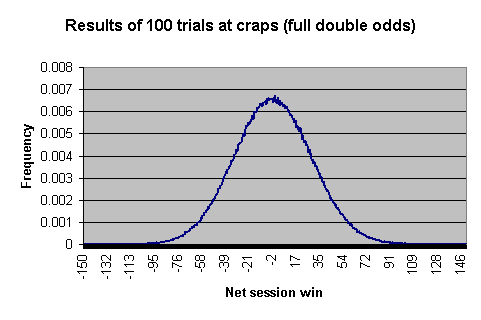
这里有一些实际数字,显示了落入各个区间的概率。
会话赢/输
| 间隔 | 可能性 |
|---|---|
| 损失超过100美元 | 0.0422% |
| 损失 76 至 100 美元 | 0.6499% |
| 损失 51 至 75 美元 | 4.6414% |
| 损失 26 至 50 美元 | 16.3560% |
| 损失 1 至 25 美元 | 30.0583% |
| 收支平衡 | 0.6743% |
| 赢取 1 至 25 美元 | 28.6368% |
| 赢取 26 至 50 美元 | 14.4257% |
| 赢取 51 至 75 美元 | 3.9097% |
| 赢取 76-100 美元 | 0.5639% |
| 赢得超过 100 美元 | 0.0418% |
该图表和表格是通过模拟 1,000,000 次 100 次试验或掷骰子并将每次试验的结果制成表格而创建的。
内部链接
- 简言之,每次下注的庄家优势是如何得出的。
- 所有主要赌注的赌场优势(按每次下注和每次掷骰计算)
- 骰子控制实验。两项关于掷骰子技巧的实验结果。
- 骰子控制优势。假设玩家能够影响骰子,则玩家拥有优势。
- 掷骰子变体。替代规则和赌注,例如 Fire Bet、Crapless Craps 和 Card Craps。
- 加州掷骰子游戏。加州人使用扑克牌来玩掷骰子游戏。
- 玩掷骰子。在圣地亚哥的 Viejas 赌场使用纸牌玩掷骰子游戏。
- 掷骰次数表。掷骰者在掷出七点之前坚持掷 1 至 200 次的概率。
- 问问巫师。查看我回答过的掷骰子问题:
- 简单的掷骰子游戏。我的简单 Java 掷骰子游戏。


