德州扑克 - 概率论 - 通用
在一场有 10 名玩家玩 50 手牌的德州扑克游戏中,同一个玩家同时拿到两张四条和一张同花顺的概率是多少?
七张牌中出现四条的概率为 0.00168067,出现同花顺的概率为 0.00027851。设 x 为出现四条的概率,y 为出现同花顺的概率,则求出的概率为 combin(50,2)*48*x 2 *y*(1-xy) 47 。答案为 0.0000421845,即 23,705 分之一。
在德州扑克中,拿到同花的概率是多少?玩家在七张牌梭哈和德州扑克中哪个更容易拿到同花?
你可以参考我关于扑克概率的部分,概率是3.03%。德州扑克和七张牌梭哈的赔率是一样的。
在德州扑克河牌圈拿到同花大顺的概率是多少?
对于那些不知道的读者来说,河牌是德州扑克中的第五张也是最后一张公共牌。玩家必须在自己的两张牌和五张公共牌之间组成最好的牌型。所以,你的问题是,玩家用七张牌组成皇家同花顺,并且第七张牌也属于皇家同花顺的概率是多少。在不考虑牌的情况下,用七张牌组成五张皇家同花顺的概率是 4*combin(47,2)/combin(52,7) = 4324/133784560,即 30940 分之一。第七张牌组成皇家同花顺的概率是 5/7。所以最终概率是 21620/936491920,即 43316 分之一。
在德州扑克中,从翻牌开始在第五街形成一个间隙或两个间隙的顺子的可能性有多大?
为了方便读者,我先问一下,如果牌堆里还剩下47张牌,用另外两张牌填补顺子中间缺口(一或两张)的概率是多少。如果缺口是1-combin(43,2)/combin(47,2) = 0.164662。如果缺口是2张,概率是4 2 /combin(47,2) = 0.0148。
在德州扑克中,如果翻牌都是相同花色,那么任何给定玩家持有另外两张相同花色的牌的概率是多少?
剩余 10 张同花色的牌,牌堆中剩余 49 张。因此,概率为 combin(9,2)/combin(49,2) = 36/1176 = 0.0306。
德州扑克和七张牌梭哈中各种牌型的概率一样吗?还是因为公共牌的不同,它们会有所不同?您能解释一下为什么吗?
是的,概率是一样的。52张牌中随机抽取7张,无论它们是如何从牌堆中抽出的,也无论你和谁分享,抽到的概率都是一样的。
在最初的两张牌中,您能告诉我在 35 手牌中获得 7 手 Ace King 或更好的牌的概率是多少吗?
拿到A/K的概率是(8/52)*(4/51) = 0.012066。拿到任意一对的概率是(3/51) = 0.058824。因此,拿到一对或更好牌的概率是0.07089。拿到恰好七手A/K或更好牌的概率是combin(35,7)*(.07089)^7*(1-.07089)^28 = 0.00772。要计算7或更大的概率,我们需要逐一计算7到35的点数。总和为0.010366551。
如果您的底牌是同花色的,您如何计算在德州扑克中翻牌时获得 4 张同花或更好的牌的概率。
再出现两张同花色牌的概率为 39*combin(11,2)/combin(50,3) = 0.109439。再出现三张同花色牌的概率为 combin(11,3)/combin(50,3) = 0.008418。因此,再出现至少两张同花色牌的概率为 0.117857。
巫师先生,首先,我要说一下,您的网站太棒了!我已经看了一段时间了。我查了一下扑克问答,没看到这个。另一个网站声称:“在德州扑克中,翻牌前拿到AK,河牌拿到A或K的概率是二分之一(均等)。”这听起来直观上太高了。您怎么看?再次感谢!
也感谢您的赞美。对于不熟悉德州扑克的人来说,这个问题类似于问,如果给玩家一张A和一张K,再加上剩余50张牌中的五张随机牌,玩家组合出K和/或A的概率是多少。其余50张牌中,有44张既不是K也不是A。从44张牌中抽出任意五张牌的方法数为combin(44,5) = 1,086,088。从全部50张牌中抽出任意五张牌的方法数为combin(50,5) = 2,118,760。因此,不组合出A和/或K的概率为1086088/2118760 = 51.26%。因此,您组合出A和/或K的概率为1-51.26% = 48.74%。这非常接近二分之一。
在德州扑克中,两个玩家拥有不同的四条的概率是多少?
两位玩家一共9张牌,其中必须包含两张四条和一张单张。组合数为 combin(13,2)*44 = 3432。从52张牌中抽出9张牌的组合数为 combin(52,9) = 3,679,075,400。因此,你拿到正确牌(但顺序不一定正确)的概率为 3432/3,679,075,400 = 1/1,071,992。
然而,仅仅因为牌是 AAAABBBBC,并不意味着两位玩家的四条牌就不同。将它们排列成一手五张牌和两手两张牌的组合方式共有 9!/(5!*2!*2!) = 756 种。以下是这 9 张牌的可能排列方式。
四条坏牌组合
玩家 1 | 玩家 2 | 翻牌 | 镜像图案 | 每个模式的组合 | 总组合数 |
AA | BB | 美国商务咨询委员会 | 2 | 72 | |
AA | AB | ABBBC | 4 | 四十八 | 192 |
AA | AA | BBBBC | 2 | 6 | 12 |
AA | 交流电 | ABBB | 4 | 12 | 四十八 |
AA | 公元前 | 支气管扩张综合征 | 4 | 24 | 96 |
AB | AB | 美国商务咨询委员会 | 1 | 144 | 144 |
AB | 交流电 | 支气管扩张综合征 | 4 | 四十八 | 192 |
其中只有第一组和第五组牌的结果会让两位玩家拿到不同的四条。因此,AAAABBBBC 组合牌出现两张不同的四条的概率为 168/756 = 22.22%。
所以你问题的答案是 (3432/3,679,075,400)*(168/756) = 4,823,963 分之一。更实际的说,派对扑克 (Party Poker) 的输牌手牌是四个“8”,就会有一个爆冷大奖 (bad beat jackpot)。假设有两张四条,两张都是“8”或更大的概率是 combin(7,2)/combin(13,2) = 21/78 = 26.92%。所以,两位玩家中任意一手牌赢得这个爆冷大奖的概率是 17,917,577 分之一。
昨晚,一位玩家在德州扑克游戏中向我提出了附加赌注。他说翻牌圈至少会出现一张人头牌(或任意三张点数),并提出等额投注。我应该接受这个赌注吗?
从40张非人头牌中抽出3张的方式数为(40*39*38)/(1*2*3) = 9880。从52张非人头牌中抽出3张的方式数为(52*51*50)/(1*2*3) = 22100。因此,抽不到人头牌的概率为9880/22100 = 44.71%。因此,抽到人头牌的概率为55.29%。他这边的赌注优势为10.58%。
假设10人玩德州扑克,使用标准的52张牌。每位玩家发完前两张牌后,“翻牌”(接下来的三张牌)全部是同花色的概率是多少?如果我手中的牌是同花色,或者每张牌都是不同花色,会有什么不同吗?
在考虑自己的牌之前,概率是 4× combin (13,3)/combin(52,3) = 5.1764706%。
换个角度来看,翻牌圈第二张牌与第一张同花色牌匹配的概率是 (12/51)。翻牌圈第三张牌与第一张同花色牌匹配的概率是 (11/50)。(12/51)×(11/50)=5.1764706%。
如果你考虑自己的牌,赔率会略有变化。如果你有两张同花色的牌,那么翻牌圈出现同花色的概率为 pr(同花色同花) + pr(不同花色同花) = combin(11,3)/combin(50,3) + 3×combin(13,3)/combin(50,3) = 5.2193878%。
如果您有两张不同花色的牌,那么翻牌成同花的概率为 pr(同花色)+ pr(不同花色的同花)= 2×combin(12,3)/combin(50,3)+ 2×combin(13,3)/combin(50,3)= 5.1632653%。
亲爱的奇才,真希望我有你的大脑。无论如何,我和统计学的斗争还在继续。我正在努力想出一个公式,用来计算翻牌圈、转牌圈和河牌圈(德州扑克)拿到同花的概率,以及我的底牌是否同花。我试过 C(50,2) / C(47,5),但河牌圈拿到同花对子却不行……我上学的时候应该多加注意!谢谢!你是我最大的粉丝
谢谢你的赞美,但我没那么聪明。几年前我参加了门萨入学考试,但没能达到要求的前2%。他们拒绝告诉我我的成绩有多好,我至今仍感到很沮丧。1月13日,《危险边缘》选拔赛将在拉斯维加斯举行,我已经预约了,但肯定也会搞砸。总之,为了回答你的问题,你现在说:
持有同花底牌:
翻牌后同花:组合(11,3)/组合(50,3)= 165/19600 = 0.842%。
转牌后同花:(combin(11,2)*39/combin(50,3))*(9/47) = 2.096%。
河牌后冲洗:(combin(11,2)*combin(39,2)/combin(50,4))*(9/46) = 3.462%。
持有非同花底牌:
翻牌后同花:0%
转牌后同花:2*combin(12,4)/combin(50,4) = 0.430%。
河牌后同花:(2*combin(12,3)*39/combin(50,4))*(9/46) = 1.458%。
这是累积概率。
持有同花底牌:
翻牌同花:0.842%。
转牌同花:2.937%。
河牌同花:6.400%。
持有非同花底牌:
翻牌圈同花:0.000%
轮流同花:0.430%。
河牌同花:1.888%。
你好,巫师,首先我想说,我很喜欢你给出的精准、没有空话的答案。话说回来,如果德州扑克的底牌是AA,翻牌是KQ9,那么凑成葫芦的概率是多少?我琢磨了好久 :( ,还是没找到一个靠谱的答案。
你可以用一张 A 和一张 K、Q 或 9 凑成葫芦。剩下 2 张 A,还有 3 张 K、Q 和 9。所以这样的组合共有 2*3*3=18 种。唯一的另一种可能性是 K、Q 或 9 对。这样的组合共有 3*combin(3,2)=9 种。所有组合数为 47*46/2 = 1081。所以概率为 (18+9)/1081 = 2.50%。
多年来我一直是你的忠实粉丝(甚至在你对扑克和体育博彩感兴趣之前),并且期待着你的每一篇“问巫师”专栏。很高兴看到你又回来了!我的问题是:在我当地的扑克室,他们会在特定时段提供“Aces Cracked, Win A Rack”活动。也就是说,如果你在他们3-6或4-8的德州扑克游戏中拿到底牌A,并且输掉了底池,赌场会给你一架筹码(100美元)。我想知道a)我拿到底牌A的频率是多少;b)如果我像我应该的那样积极地玩,他们会输掉多少次;c)是不是最好一直过牌,希望输掉,因为100美元通常比底池的金额要好。如果你能提供任何数据,那就太好了,永远感激不尽!再次感谢,继续为大众提供启发!
谢谢你的赞美。你在任何一手牌中拿到底牌 A 的概率是 6/1326,也就是每 221 手牌一次。根据我的十人德州扑克部分 (/games/texas-hold-em/10players.html),假设所有玩家都坚持到最后,用底牌 A 获胜的概率是 31.36%。但这只是一个假设。如果非要我猜的话,我估计在真正的十人游戏中用 A 获胜的概率大约是 70%。所以拿到底牌 A 然后输掉的概率是 0.3*(1/221) = 0.1357%。所以,按每次 100 美元计算,每手牌损失 13.57 美分。超过 10 人,扑克室平均每手牌损失 1.36 美元,这会大幅降低抽水。我倾向于同意你的跟注策略,这会让更多玩家留在牌局中,并增加你输钱的几率。
首先,我要感谢你们提供这么棒的网站。现在我的问题是:我们正在玩德州扑克,翻牌圈用两张小牌组成了同花听牌。我们都知道击中同花的概率,但我们真正想知道的是赢牌的概率。假设我们确定有人的同花牌比我们大。那么我的问题是,如果只亮出一张同花牌而不是两张,那么亮出的概率是多少?此致
不用客气。所以翻牌后,你拿到了四张同花,牌面还有两张。拿到所需花色的概率是 9*38/ combin (47,2) = 342/1081 = 31.64%。
在德州扑克游戏中,当河牌圈恰好有三张同花的公共牌时,我想知道另一位玩家拿到两张同花牌,从而组成比我更大的同花的概率。例如,如果我拿到黑桃89,公共牌包括黑桃3、黑桃7和黑桃K,那么牌堆里有4张黑桃比我的9大(TJQA)。假设是9人游戏,那么有人拿到两张黑桃,其中至少有一张更大的黑桃,这种概率是多少?如果只有2张(或3张或x张)黑桃比我最大的底牌大呢?感谢您的帮助和这个很棒的网站。
下表显示了1至8个高段位玩家和2至10个玩家(包括你自己)的概率。以你举的这个例子,高段位玩家4个,总共9个玩家,概率为16.45%。我计算这些概率时假设了牌局之间的独立性,虽然这并不是一个正确的假设,但结果应该是一个接近的估计值。
更高同花的概率更高排名(向下)按玩家总数(横向)巫师估计
| 更高级别 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0.71% | 1.41% | 2.11% | 2.80% | 3.49% | 4.17% | 4.85% | 5.52% | 6.19% |
| 2 | 1.31% | 2.61% | 3.89% | 5.15% | 6.40% | 7.62% | 8.84% | 10.03% | 11.22% |
| 3 | 1.82% | 3.60% | 5.36% | 7.08% | 8.77% | 10.43% | 12.05% | 13.65% | 15.22% |
| 4 | 2.22% | 4.40% | 6.52% | 8.60% | 10.63% | 12.61% | 14.56% | 16.45% | 18.31% |
| 5 | 2.53% | 4.99% | 7.39% | 9.72% | 12.00% | 14.23% | 16.39% | 18.50% | 20.56% |
| 6 | 2.73% | 5.38% | 7.96% | 10.47% | 12.91% | 15.29% | 17.60% | 19.85% | 22.03% |
| 7 | 2.83% | 5.58% | 8.25% | 10.84% | 13.36% | 15.81% | 18.20% | 20.51% | 22.76% |
| 8 | 2.83% | 5.58% | 8.25% | 10.84% | 13.36% | 15.81% | 18.20% | 20.51% | 22.76% |
更高同花顺的概率按玩家总数(横向)排名更高(向下)Miplet 模拟
| 更高级别 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0.69% | 1.41% | 2.12% | 2.83% | 3.54% | 4.25% | 4.96% | 5.66% | 6.36% |
| 2 | 1.28% | 2.60% | 3.91% | 5.21% | 6.48% | 7.77% | 9.05% | 10.31% | 11.56% |
| 3 | 1.79% | 3.61% | 5.41% | 7.19% | 8.92% | 10.68% | 12.41% | 14.11% | 15.79% |
| 4 | 2.19% | 4.40% | 6.58% | 8.75% | 10.85% | 12.94% | 15.01% | 17.04% | 19.04% |
| 5 | 2.50% | 5.00% | 7.47% | 9.92% | 12.28% | 14.63% | 16.94% | 19.21% | 21.43% |
| 6 | 2.71% | 5.40% | 8.06% | 10.69% | 13.23% | 15.74% | 18.23% | 20.65% | 23.03% |
| 7 | 2.81% | 5.61% | 8.36% | 11.08% | 13.70% | 16.30% | 18.86% | 21.37% | 23.82% |
| 8 | 2.81% | 5.61% | 8.36% | 11.08% | 13.70% | 16.30% | 18.86% | 21.37% | 23.82% |
很棒的网站。我只是想了解一下个人情况。我当时正在玩一场四人德州扑克。我拿到了底牌A。河牌圈我拿到了同花大顺。我想知道一开始就拿到A,在河牌圈拿到同花大顺的概率是多少?
谢谢。假设皇家牌由你的两张A中的一张组成,那么在河牌圈组成皇家牌的概率是2*46=92。这包括你底牌A的两种花色以及额外牌的46种可能性。从50张牌中发出5张,一共有(50,5) = 2,118,760种组合方式。所以概率是92/2,118,760 = 23,030分之一。
如果翻牌圈出现三张相同花色的牌,而我没有与翻牌圈花色匹配的牌,并且牌桌上还剩下十名玩家,那么有人拿到同花的概率是多少?
任何一位玩家拿到同花的概率是combin (11,2)/combin(49,2) = 55/1176 = 4.68%。假设每手牌之间相互独立(但事实并非如此),那么9位玩家没有拿到同花的概率是 (1 − 0.0468%) 9 = 64.98%。因此,至少有一位玩家拿到同花的概率是 1-0.6498 = 35.02%。这只是一个快速估算。如果我进行随机模拟,我认为概率会略高一些,因为每手牌之间相互依赖。
亲爱的巫师先生,我最近一直在计算德州扑克中,如果拿到两张同花的底牌,拿到同花的概率是多少?我的答案一直是5.8%,但这似乎最终是错误的,非常感谢您的帮助。
同花,即有三张牌与你的底牌花色相同,其概率为: combin (11,3)×combin(39,2)/combin(50,5) = 122265/2598960 = 0.057706。同花,即有另外四张牌与你的底牌花色相同,其概率为:combin(11,4)×combin(39,1)/combin(50,5) = 2145/2118760 = 0.001012。同花,即有另外五张牌与你的底牌花色相同,其概率为:combin(11,5)/combin(50,5) = 462/2118760 = 0.000218。在公共牌上完成其他花色同花的概率是 3×combin(13,5)/combin(50,5) = 3861/2118760 = 0.001822。将这些数字相加,可得出 0.057706 + 0.001012 + 0.000218 + 0.001822 = 0.060759。
在德州扑克中,出现“破牌”的概率是多少?也就是说,公共牌上五张牌既没有对子,也没有同花,也没有顺子。
棋盘上五个不同等级的组合数为combin (13,5)*4 5 = 1287 × 1024 = 1,317,888。
这五个点数代表三种花色、两种花色中的两种以及一种花色中的一种的概率为 combin(4,2)*2*combin(5,2)*combin(3,2)=360。Combin(4,2) 表示对于出现两次的花色,从四种花色中选出两种的方式数。2 表示对于出现一次的花色,从两种方式中选出两种的方式数。Combin(5,2) 表示对于两张牌中的第一种花色,从五种花色中选出两种的方式数。4 5表示对于另外两种花色,从剩下的三种花色中选出两种的方式数。
这五个点数代表四种花色、两种花色中的一种以及一种花色中的三种的概率是 4*combin(5,2)*3*2=240。4 表示对于出现两次的花色,从四种花色中选出一种花色的方式数。Combin(5,2) 表示对于该花色的两张牌,从五种花色中选出两种的方式数。3 表示对于第一种花色,从剩下的三种花色中选出一种的方式数。2 表示对于第二种花色,从两种花色中选出一种的方式数。
将四种花色的牌排列在五个不同的等级上,共有 4 5 =1024 种方法。
因此,出现不超过两张相同花色的牌的概率为 (360+240)/1024 = 600/1024 = 58.59%。
从 13 个等级中排列出 5 个等级,一共有 (13,5)=1287 种组合方式。其中没有三个等级在 5 的范围内的组合数量是 79。这个问题没有简单的公式。我不得不循环遍历所有组合。因此,等级之间足够间隔的概率是 79/1287 = 6.14%。
因此,破损板的概率为 (1317888/2596960)*(600/1024)*(79/1287) = 1.825211%。
我被质疑破发顺子的数量。以下是所有79个可能的破发顺子的列表。
| 2378Q 2378千 2379Q 2379千 237TQ 237TK 237JQ 237JK 237QK 2389千 238TK 238JK 238QK 2479Q 2479千 247TQ 247TK 247JQ 247JK 247QK | 2489千 248TK 248JK 248QK 257TQ 257TK 257JQ 257JK 257QK 258TK 258JK 258QK 267JQ 267JK 267JA 267QK 267QA 267KA 268JK 268JA | 268QK 268QA 268KA 269JA 269QA 269KA 278QK 278QA 278KA 279QA 279KA 289KA 3489千 348TK 348JK 348QK 358TK 358JK 358QK 368JK | 368JA 368QK 368QA 368KA 369JA 369QA 369KA 378QK 378QA 378KA 379QA 379KA 389KA 469JA 469QA 469KA 479QA 479KA 489KA |
我在印第安纳州凯撒赌场玩德州扑克。他们有一个“爆冷大奖”(Bad Beat Jackpot),现在四张或更好的牌会被爆冷。两位玩家都必须打出两张底牌,并且必须有四位玩家拿到牌。我的问题是,假设所有玩家都坚持到最后,任何一手牌成为爆冷牌的概率是多少?
我的新Bad Beat Jackpot 部分显示,在 10 人游戏中出现这种 bad beat 的概率为 0.0000108,即大约 93,000 分之一。
在您的终极德州扑克回报表中,为什么对于表中列出的预期回报为负的两张牌,建议大幅加注?例如同花K/2。
根据我的双人德州扑克概率,同花 K/2 的可能结果如下:
胜率 51.24%
损失44.82%
抽奖 3.94%
我的终极德州扑克赌桌显示,玩家在“玩牌”投注上占有优势,但在“底注”和“盲注”投注上处于劣势。在这种情况下,玩家的“底注”和“盲注”投注赔率很低。然而,他在“玩牌”投注上的赔率很有利。因此,通过最大限度加注,他可以从超过50%的胜率中获得最大价值。其他两个投注的低赔率使总价值低于50%。如果加注幅度较小,这个价值会更低。
在2008年世界扑克大赛中,万渊元之的四A被贾斯汀·菲利普的皇家同花顺击败。我有个关于这种情况发生的概率的简单问题。ESPN和其他媒体称,发生这种情况的概率约为27亿分之一。在我看来,他们只是把公布的四A出现的概率乘以皇家同花顺出现的概率。这是正确的计算方法吗?
我也不同意27亿分之一这个数字。正如你所说,他们似乎独立计算了每个玩家的概率,只针对两个玩家都使用底牌的情况,然后相乘。用这种方法,我得到的概率是0.000000000341101,大约是29亿分之一。也许27亿分之一的概率也涉及到对两个玩家概率的舍入误差。他们显然也忘了把概率乘以2,原因我稍后会解释。
四张 A 输给同花大顺有以下三种可能情况。
情况 1:一名玩家有两张同花大顺,另一名玩家有两张 A,并且牌面上有另外两张 A、另外两张同花大顺牌以及任何其他牌。
例子:
玩家 1:

玩家 2:

木板: 




在大多数扑克室里,要想赢得爆冷大奖,赢家和输家都必须用掉两张底牌。视频里的爆冷也属于这种类型;事实上,这些牌型也正是爆冷的。
情况 2:一名玩家有两张同花大顺 (TK),另一名玩家有一张 A 和一张“空白”牌,并且牌面上有另外三张 A 和另外两张同花大顺牌。
例子:
玩家 1:

玩家 2:

木板: 




情况 3:一名玩家有一张同花大顺 (TK) 和一张空白牌,另一名玩家有两张 A,并且牌面上有另外两张 A 和另外三张同花大顺的牌。
例子:
玩家 1:

玩家 2:

木板: 




下表显示了玩家和棋盘每种情况的组合数。右下角单元格显示组合总数为 16,896。
坏节拍组合
| 案件 | 玩家 1 | 玩家 2 | 木板 | 产品 |
|---|---|---|---|---|
| 1 | 24 | 3 | 四十四 | 3,168 |
| 2 | 24 | 132 | 1 | 3,168 |
| 3 | 704 | 3 | 1 | 2,112 |
| 全部的 | 8,448 |
然而,即使我们把两位玩家的牌都反过来,仍然可能出现爆牌。所以,我们应该将组合数乘以2。调整后,总有效组合数为2 × 8,448 = 16,896。
双人德州扑克所有组合的总数为( 52,2) × (50,2) × (48,5) = 2,781,381,002,400。因此,四张 A 输给同花大顺的概率为 8,448/2,781,381,002,400 = 0.0000000060747,约为 1.65 亿分之一。单次爆冷的概率为 4.39 亿分之一。赔率没有视频中报道的那么低,原因很简单,因为两手牌有重叠,共用一张 A。换句话说,这两个事件呈正相关。
根据《揭露纽约视频扑克的真相》一文,您说得完全正确。玩家的结果确实是命中注定的。无论玩家持有什么牌,都无法逃脱命运的安排。如果玩家试图故意逃避命运,游戏会使用守护天使功能来纠正玩家的错误。我完全同意作者的观点,这类游戏应该警告玩家,他们玩的不是真正的视频扑克,赔率表只是玩家实际赔率的无意义衡量标准。另外,还要注意的是,这类假视频扑克机并非纽约独有。
您好,我是来自夏威夷的七年级学生。我正在做一个关于扑克和洗牌的科学展览项目。我正在使用您制作的图表,该图表是根据游戏中的玩家人数来计算底牌德州扑克牌型的胜率。希望您能回答几个问题,帮助我完成我的项目:
- 您是如何得出图表中的百分比的?
- 如果您使用了计算机程序,您是如何开发它的,花了多长时间?
- 您说过,您创建“概率魔法师”是出于爱好。随着您的网站越来越出名,您的实验方式有没有改变?为什么?
- 两人桌的牌局是用一个强力循环程序完成的,它循环了所有1225张可能的对手牌和1,712,304张可能的公共牌。对于三到八名玩家来说,循环会耗费大量的时间,所以我做了一个随机模拟。
- 我几乎所有的程序都是用 C++ 写的,包括我刚才提到的两个程序。其余的都是用 Java 或 PERL 写的。我大部分代码都是从其他扑克程序里复制粘贴过来的。新代码看起来只需要一天就能写完。
- 是的,我于1997年6月出于爱好创建了我的网站。直到2000年1月,我才开始接受广告,并尝试将其发展成一门生意。多年来,它经历了三个不同的域名。这是它在1999年5月的样子。网站的宗旨始终如一,即提供基于数学的赌博策略资源。这些年来,我一直在不断添加更多游戏和素材。我曾经尝试过提供2005赛季的NFL选秀信息,但最终以失败告终。
你好,巫师。我看了你的德州扑克问题,发现你计算出,当你手里拿着底牌Q时,在牌面上看到A或K的概率是59.85%。你是怎么得出这个数字的?
一副牌中剩余的50张牌,五张牌的组合数共有(50,5)=2,118,760种。其中42张牌是2-Q。42张牌中五张牌的组合数为(42,5)=850,668种。因此,没有拿到K或A的概率为850,668/2,118,760 = 40.15%。因此,至少拿到一张A或K的概率为1-40.15% = 59.85%。
另一种计算方法是 1 - pr(翻牌中第一张牌不是 A 或 K) × pr(翻牌中第二张牌不是 A 或 K) × pr(翻牌中第三张牌不是 A 或 K) × pr(翻牌中第四张牌不是 A 或 K) × pr(翻牌中第五张牌不是 A 或 K) = 1 - (42/50) × (41/49) × (40/48) × (39/47) × (38/46) = 59.85%。
在德州扑克中,如果我手里有两张同花色的牌,那么我在翻牌时再次拿到两张相同花色的牌的概率是多少?
再凑成两张同花色的牌,组合数有 (11,2)=55 种,凑成一张不同花色的牌则有 39 种。翻牌圈的牌型组合共有 (50,3)=19,600 种。因此,翻牌圈凑成同花的四张牌的概率为 55×39/19,600 = 10.94%。
我参加了一局在线扑克游戏,想知道发生这种情况的几率,请问:
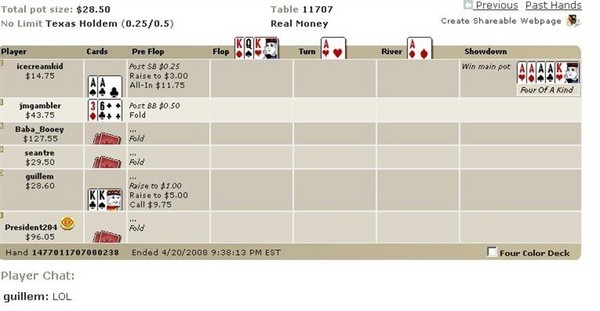
通常情况下,我厌倦了关于爆冷门(bad beat)的问题,但这道题实在太难了,我实在无法忽视。在一场双人游戏中,如果双方都有底牌对子,那么在第一张牌发出之前,四张K被四张A击败的概率是 2 * combin (4,2) * combin (4,2) * 44 / ( combin (52,2) * combin (50,2) * combin (48,5)) = 2 * 6 * 6 * 44 / ( 1326 * 1225 * 1712304) = 877,961,175 分之一。这是一场六人游戏,所以共有 combin (6,2) = 15 种不同的玩家对子。在六人游戏中,这个概率要高出 15 倍,即 58,530,745 分之一。发出所示底牌后,翻牌前,该手牌以原样结束的概率为 38,916 分之一。
拉斯维加斯一家牌室正在推出一项促销活动:凑齐四种花色的同花,即可赢得400美元。你必须用两张底牌,并且有五小时的限时时间。假设每小时35手牌,时钟从第一次同花开始计时,那么在五小时内凑齐另外三次同花的概率是多少?谢谢。
假设你的第一手同花是黑桃。每小时35手,五小时内可以玩175手。那么你就有175手牌来组成红桃、方块和梅花的同花。我假设玩家永远不会放弃任何有可能组成他需要的花色之一的同花的牌。
使用两张底牌凑成特定花色(比如红桃)的同花的概率为:combin(13,2)×[combin(11,3)×combin(39,2) + combin(11,4)×39 + combin(11,5)]/(combin(52,2)×combin(50,5)) = 10576566/2809475760=0.003764605。在接下来的175手牌中,凑不成红桃同花的概率为 (1-0.003764605) 175 =0.51682599。
假设其他三张牌凑不齐的概率为pr(无红桃同花)+pr(无方块同花)+pr(无梅花同花)是不正确的,因为你会重复计算凑不齐其中两张牌的概率。所以你应该加上pr(无红桃或方块同花)+pr(无红桃或梅花同花)+pr(无梅花或方块同花)。然而,这会错误地多减未能凑齐所有三张牌的概率。所以你应该加上pr(无梅花、方块或红桃同花)。
进行 175 手牌并且从未获得任何两张特定花色的概率是 (1-2×0.003764605) 175 =0.266442448。
进行 175 手牌并且永远无法获得剩余三种花色的概率是 (1-3×0.003764605) 175 =0.137015266。
所以答案是 1-3×0.51682599 + 3×0.266442448 - 0.137015266 = 0.111834108。
非常感谢dwheatley对这个问题的帮助。这个问题在我的“Wizard of Vegas ”论坛上讨论过。
多伊尔·布伦森(Doyle Brunson)在1976年和1977年两次赢得世界扑克锦标赛主赛事冠军。他每次都拿着10-2的底牌,并且两次都在河牌圈拿到了葫芦。这到底有多大的概率呢?
给定两张不同点数的牌,凑成葫芦的概率是1/121.6。河牌凑成葫芦的概率是1/207。
在两次河牌圈中拿到这种牌的概率是 43,006 分之一。
如果起始牌是相同的两张牌(仅在等级上),则发生这种情况的概率为 3,564,161 分之一。
两次都恰好出现 10-2 的概率是 295,379,826 分之一。
刚从退伍军人协会的扑克之夜回来。连续三次拿到6-6!以前从未发生过这种情况。一个晚上连续三次拿到同点数的口袋对的概率是多少?你可以假设一个晚上总共有120轮。
答案和解决方案出现在以下剧透标签中。
[/spoiler]在任何给定时间,您可能处于四种状态:
- 状态 1:第一手牌或最后一手牌不是口袋对的任何一手牌。
- 状态 2:最后一手牌是一对底牌。
- 状态 3:最后两手牌是相同的底牌对。
- 状态 4:已经连续出现三个相同的口袋对。
如果你处于状态 1,那么你进入状态 2 的概率是 3/51。否则,你仍处于状态 1。
如果你处于状态 2,那么你可以以 (4/52)×(3/51) 的概率进入状态 3。否则,你将返回状态 1。
如果你处于状态 3,那么你可以以 (4/52)×(3/51) 的概率进入状态 4。否则,你将回到状态 1。
如果您处于状态 4,则您留在那里。
也就是说,您可以按如下方式创建转换矩阵 T:
| 0.941176 | 0.058824 | 0.000000 | 0.000000 |
| 0.941176 | 0.054299 | 0.004525 | 0.000000 |
| 0.941176 | 0.054299 | 0.000000 | 0.004525 |
| 0.000000 | 0.000000 | 0.000000 | 1.000000 |
总共玩了 120 手牌,因此求出 T^120。
| 0.941044 | 0.058549 | 0.000265 | 0.000141 |
| 0.941025 | 0.058548 | 0.000265 | 0.000162 |
| 0.936786 | 0.058284 | 0.000264 | 0.004666 |
| 0.000000 | 0.000000 | 0.000000 | 1.000000 |
右上角的单元格向我们展示了从状态 1 开始,在三手序列中经过 120 手起手牌后进入状态 4 的概率,即 0.000141471。
取该数字的倒数,概率是 7068.605131 分之一。
[/spoiler]这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
在电影《皇家赌场》中,在扑克锦标赛的最后一手牌中,四名玩家的牌型如下:
- 冲洗
- 客满
- 满堂红(与第一个不同)
- 同花顺
这种情况的概率有多大?
我不得不为此进行模拟。在我的模拟中,我假设没有人会弃牌。在近22亿轮的模拟中,这种情况发生了312次。这相当于大约七百万分之一的概率。


