概率 - 骰子
如果您掷 6 个六面标准骰子,掷出六个相同点数的概率是多少?
答案是 6*(1/6) 6 = 6/46,656 = 1/7,776 =~ 0.0001286 。
投掷者平均要投掷多少次才能掷出“7”?我知道每投掷6次就会出现一次7,但考虑到7-11和掷骰子游戏,再加上投掷者可能多次掷出点数,我认为平均投掷次数可能会高于预期。有没有这方面的数学参考资料?
每位玩家平均掷骰次数为8.525510次。要了解掷骰次数恰好为2到200次的概率,请参阅我的掷骰子生存概率页面。
在 100,000 次掷骰子(掷骰子/不通过线)中,连续输掉 2 次、3 次、4 次、5 次、6 次、7 次、8 次或 9 次 DP 赌注的几率(和频率)是多少。
我的掷骰子附录展示了如何计算任意一次下注的赔率。你会看到,不及格投注的输掉概率是 2928/5940。连续输掉 n 次投注的概率是 (2928/5940) n 。100,000 次投注中恰好输掉 n 次的概率可以近似为 100,000 * (2928/5940) n+2 。
一次掷六个骰子掷出相同数字的概率是多少?
用六个骰子掷出六个相同数字的概率是 6*(1/6) 6 =1/7776 =~ 0.01286%。
你掷一对骰子28次不掷出7的概率是多少?你是怎么算出来的?恭喜你的网站,太棒了。
谢谢你的赞美。我猜你的意思是,掷一对骰子28次都不掷出7的概率是多少。任何一次掷出7的概率是5/6。28次掷出7的概率是(5/6) /28 = 0.006066,大约是1/165。
想问一下关于东方骰子游戏的问题。游戏中玩家需要猜测骰子的哪一面朝上。玩家首先在1、2、3、4、5、6上投注(类似轮盘赌),然后“庄家”会同时掷3个骰子。如果所选数字出现一次(在3个骰子中的任何一个上),赔率为1:1;如果所选数字出现两次,赔率为2:1;如果所选数字同时出现在3个骰子上,赔率为3:1。由于玩家可以任意下注,那么最佳下注数是多少?(假设我所有赌注的数额相同)
巫师先生,掷四个骰子时掷出两对的概率是多少?
可能的组合有 (6,2)=15 种不同的对子组合。掷出任意特定的两对,骰子有 (4,2)=6 种不同的组合方式。掷四个骰子,一共有 6^4=1296 种不同的组合方式。因此,概率为 90/1296=6.9444%。
如果我掷一个骰子,掷出六点的概率是 1/6。如果我掷两个骰子,其中一个掷出六点的概率会增加,还是保持在 1/6?
如果你掷了 x 个骰子,那么至少掷出一个 6 的概率是 1-(5/6) 2 。如果掷的是两个骰子,那么这个概率就是 30.56%。
使用 6 个骰子掷出 3 个 1 有多少种不同的方法?
首先,有 (6,3)=20 种组合方法,可以从 6 个骰子中选出 3 个,作为三个 1。然后,其他 3 个骰子可以分别代表 5 个数字。因此,总共有 20×5 3 =2500 种组合方法。掷出所有骰子的方法总数为 6 6 =46,656 种,因此掷出三个 1 的概率为 2500/46656=0.0536。有关组合函数的帮助,请参阅我在扑克部分提供的概率。
三个骰子同时掷,任意一个骰子点数为1的概率是多少?我的理解应该是50%(1/6+1/6+1/6=1/2 -->50%),但你的赔率表显示的是34.72%。请帮忙。
用三个骰子掷出恰好一个“1”的概率是 3*(5/6) 2 *(1/6) = 75/216 = 34.72%。
抛 4 个骰子时掷出“对子”的概率是多少?
这对数字可以是 6 个数字中的任意一个。另外两个单数可以是其他五个数字中的任意一个。因此,已经有 6*combin(5,2)=60 种组合。有 combin(4,2)=6 种骰子组合可以出现这对数字。这两个单数可以以两种方式排列。因此,共有 60*12=720 种投掷方法。所有投掷方法总数为 6 4 =1296。因此,概率为 720/1296 =~ 55.56%。
我朋友开了一家酒吧,他有一种“每日奶昔”,特百惠容器里装着十颗骰子,请问一下,一次摇晃就能匹配十颗骰子中的八颗的概率是多少?谢谢您的宝贵时间。
掷 10 个骰子,恰好有 8 个数字相同的概率为 6*combin(10,8)*(1/6) 8 *(5/6) 2 = 1/8957.952。至少有 8 个数字相同的概率为 6*[combin(10,8)*(1/6) 8 *(5/6) 2 + combin(10,9)*(1/6) 9 *(5/6) + (1/6) 10 ] = 1/8569.469。
我最近在玩西洋双陆棋时,连续四次掷出双六。这种情况再次发生的概率是多少?
每次新掷骰子时,接下来四次掷骰子均为双六的概率为 (1/36) 4 = 1/1679616。
一次掷 5 个骰子得到顺子的概率是多少?
有两种可能的跨度:1 到 5 和 2 到 6。每种跨度都有 5!=120 种排列方式。掷五个骰子共有 6 *5 = 7776 种方法。因此概率为 2*120/7776 = 3.09%。在玩 Yahtzee 时,当我把 0 标记为大顺子后,这个概率似乎高了很多。
一个面公平的骰子被掷了30次。数字1出现的预期次数是多少?数字1出现的概率是多少?
预期的 1 的数量是 30*(1/6) = 5。恰好出现 5 个 1 的概率是 combin(30,5)*(1/6) 5 *(5/6) 25 = 19.21%。
如果我有任意数量的骰子,那么如果我掷出所有骰子,至少有一个骰子落在 1 上的概率是多少?
骰子点数不全为 1 的概率是 (5/6) n 。因此,至少有一个点数为 1 的概率是 1-(5/6) n 。我们以五个骰子为例。答案是 1-(5/6) 5 = 59.81%。
如果我掷 36 个骰子,至少掷出一个六点的概率是多少?
1-(5/6) 36 = 99.86%
如果我继续掷骰子,每次都将六点全部去掉,那么我如何预测特定次数的掷骰子后剩余的理论骰子数量?
每次投掷,预期剩余骰子数量为 5/6。因此,投掷 n 次后剩余骰子数量的预期值为 36*(5/6) n 。例如,投掷 10 次后,平均剩余骰子数量为 5.81 个。
如果我掷三个骰子,至少有两个数字相同的概率是多少?
所有数字不同的概率是 (5/6)*(4/6)=20/36。因此,至少有两个数字相同的概率是 1-(20/36) = 16/36 = 44.44%。
如果两个人掷一对骰子,掷出相同数字的概率是多少?有没有公式可以计算?
是的。你只需计算从 2 到 12 的所有数字,并确定每个数字掷出两次的概率。所以答案是 (1/36) 2 + (2/36) 2 + (3/36) 2 + (4/36) 2 + (5/36) 2 + (6/36) 2 + (5/36) 2 + (4/36) 2 + (3/36) 2 + (2/36) 2 + (1/36) 2 = 11.27%。
我最近参加了一个医院庆祝活动。奖品是,如果一次掷出7个骰子,出现7个六,就能赢得一辆新车。每次1英镑。这概率肯定很高,但究竟有多高呢?
用七个骰子掷出七个六的概率是 (1/6) 7 = 279,936 分之一。所以,这辆车的价值必须达到 279,936 英镑或更高,这才是一个好的赌注。即使是普通的劳斯莱斯也不值这么多钱,所以我认为这是一场糟糕的赌注。
[Bluejay 补充道:呃,是的,但我觉得重点是这是为了慈善事业。哪个更有趣:捐 1 英镑给慈善机构,除了帮忙的快感什么也得不到,还是捐 1 英镑,除了快感之外,还有赢得一辆车的几率?]
掷五个骰子,得到 5 条、4 条、3 条、葫芦、2 对、一对、顺子和零的概率是多少?
- 五张同点牌:6/6 5 = 0.08%(显而易见)
- 四张同点牌:5*6*5 = 1.93%(单张的 5 种可能位置 * 四张同点牌的 6 种等级 * 单张的 5 种等级)。
- 葫芦:combin(5,3)*6*5/6 5 = 3.86%(combin(5,3) 三条的位置 * 三条的 6 个等级 * 对子的 2 个等级)。
- 三张同点牌:COMBIN(5,3)*COMBIN(2,1)*6*COMBIN(5,2) / 6 5 = 15.43%。(combin(5,3) 三张同点牌的位置 * combin(2,1) 较大单张牌的位置 * 三张同点牌的 6 个等级 * combin(5,2) 两个单张牌的等级。)
- 两对:COMBIN(5,2)*COMBIN(3,2)*COMBIN(6,2)*4 / 6 5 = 23.15%(较高对的组合(5,2) 位置 * 较低对的组合(3,2) 位置 * 两对的组合(6,4) 排名 * 单对的 4 排名)。
- 配对:COMBIN(5,2)*fact(3)*6*combin(5,3) / 6 5 = 46.30%(配对的 combin(5,2) 位置 * 三个单例的 fact(3) 位置 * 配对的 6 个等级 * 单个的 combin(5,3) 等级)。
- 直线:2*fact(5) / 6 5 = 3.09%(直线的2个跨度{1-5或2-6} * fact(5) 方式排列顺序)。
- 无:((COMBIN(6,5)-2)*FACT(5)) / 6 5 = 6.17%(combin(6,5) 种方法从六个等级中选择五个等级,减去 2 个直线等级,* fact(5) 种方法来排列顺序。
你好,巫师,我想知道你能不能回答这个问题。在17世纪法国流行的一种赌博游戏中,玩家会掷一对骰子24次。如果至少有一次掷出双六,他就赢了。当时关于获胜概率是高于还是低于50%存在争议。你能帮我吗?
当然,这很简单。24 次投掷中至少掷出一个 12 的概率是 1-(35/36) 24 = 49.14%。因此,押注 12 的赔率更高。这是一个聪明的赌注,因为 24 次投掷中 12 的预期次数是 2/3。然而,这并不意味着掷出 12 的概率就是 2/3,因为有时会掷出不止一个 12,而押注 12 的玩家在掷出第一个 12 之后不会再赢任何额外的 12。假设每次投掷的获胜概率为 p,投掷次数为 n,至少赢一次的概率为 w,那么用 p 和 w 来解 n 可得……
w=1-(1-p) n
1-w = (1-p) n
log(1-w) = log((1-p) n )
log(1-w) = n*log(1-p)
n= log(1-w)/log(1-p)
所以在你的例子中,n = log(1-.5) / log(1-(1/36)) = log(0.5) / log(35/36) = 24.6051。所以,如果24.6次投掷的成功概率是50%,那么24次投掷的成功概率肯定会略低。
用六个骰子连续六次掷出 1、2、3、4、5、6 的概率是多少?
一次掷六个骰子,掷出 123456 的概率可以表示为:prob(第二个骰子与第一个骰子不匹配) * prob(第三个骰子与第一个或第二个骰子都不匹配) * ... = 1*(5/6)*(4/6)*(3/6)*(2/6)*(1/6) = 0.015432。因此,连续六次掷出 123456 的概率为 0.015432 6 = 74,037,208,411 分之 1。
如果我掷一个骰子 6 次,那么恰好 4 次出现“2”的概率是多少?
合并(6,2)*(1/6) 4 *(5/6) 2 = 0.008037551。
如果允许你保留掷出的最高的三个骰子,那么用 3、4 和 5 个骰子掷出 13 或更大的概率是多少?
概率如下:
3个骰子:25.93%
4个骰子:48.77%
5个骰子:66.13%。
假设我们掷三个公平的六面骰子。假设三个骰子点数之和为 12,那么第一个骰子点数为 4 的条件概率是多少?
给定B,A的概率等于A和B的概率除以B的概率。在这种情况下,第一个骰子掷出4,然后另外两个骰子掷出总点数8的概率是(1/6)*(5/36) = 5/216。3个骰子掷出总点数12的概率是25/216,正如我的骰宝部分所示。所以答案是(5/216)/(25/216) = 5/25 = 20%。
在最近的一次编程练习中,我和其他学生被要求用代码描述一个六面骰子,然后用我们的骰子来玩一个简单的游戏。游戏的目标是掷骰子,直到掷出点数之和正好达到 100。任何使点数超过 100 的点数都不会被添加,而只是被添加到统计数据中。很快,我们确定,达到 100 所需的最少掷骰次数是 17 次。然而,计算这种情况发生的概率却一直难以捉摸。计算特定掷骰顺序的概率相当简单,但如何将非特定的掷骰顺序以及在 17 次掷骰中达到 100 的不同方式(16*6 + 1*4 和 15*6 + 2*5)结合起来呢?
您提到的两种方法是掷 17 次总共掷出 100 的唯一方法。掷出 16 个六和一个四的概率是 17*(1/6) 17 。4 有 17 种可能的位置,每种序列的概率为 (1/6)*(1/6)*...*(1/6),共 17 项。掷出 15 个六和 2 个五的方法数为(17,2) = 136。因此,掷出 15 个六和 2 个五的概率是 136*(1/6) 17 。所以总概率为 (17+136)*(1/6) 17 。= 1/110,631,761,077。
有3个骰子,其中2个是真正的六面骰子,1个是所有面都是6的骰子。所有骰子都在我的口袋里。我随机拿出一个骰子掷了出去。结果是6。请问这个骰子是真正的六面骰子的概率是多少?
设 A = 选择正常骰子
设 B = 用随机选择的骰子掷出 6
答案 = Pr(A 给定 B) = Pr(A 和 B)/pr(B) = ((2/3)*(1/6))/((2/3)*(1/6)+(1/3)*1) = (2/18)/((2/18)+(6/18)) = 1/4。
如果只能掷一次六个骰子,那么以任意顺序掷出 6、6、6、6、1 和 4 的概率是多少?
有 6!/(4!*1!*1!) = 30 种方法可以按任意顺序排列这些数字。换一种理解,有 6 个位置可以放置 1,剩下 5 个位置可以放置 4,所以 6*5=30。以这个顺序得到 666614 的概率是1/6 = 1/46656。将这个概率乘以 30,得出 30/46656 = 0.0643%,即 1/1552.2。
我理解的事件“等待时间”是该事件概率的倒数。我感兴趣的是计算用一个骰子掷出连续2的等待时间。在模拟中,我平均掷出42次。我该如何将其与掷出连续2的概率联系起来?
对于单个事件,如果概率为 p,则平均等待时间为 1/p,这的确没错。然而,对于连续事件,情况会变得更加复杂。设 x 表示最后一次掷出的结果不是 2 的状态。这也是初始状态。设 y 表示最后一次掷出的结果为 2 的状态。第一次掷出结果后,我们有 5/6 的概率仍处于状态 x,有 1/6 的概率处于状态 y。设 Ex(x) 表示从状态 x 开始的掷骰次数的预期,Ex(y) 表示从状态 y 开始的掷骰次数的预期。那么……
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y),且
Ex(y) = 1 + (5/6)*ex(x)
求解这两个方程...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*( 1 + (5/6)*Ex(x))
Ex(x) = 7/6 + (35/36)*Ex(x)
(1/36)*Ex(x)= 7/6
例如(x)= 36 *(7/6)= 42
因此连续两次掷出 2 的平均等待时间为 42 次。
我遇到了相同类型的问题,只有预期翻转才能得到两次正面,在我的数学问题网站上,请参阅问题 128。
你能告诉我用两个、三个和四个骰子掷出两个相同数字的概率吗?我想知道,一次需要掷多少个骰子才能使赔率站在掷骰子的人这边。(哪个数字翻倍都无所谓。)
根据掷骰次数,出现至少一个数字多次的概率如下:
一对或多对的概率
| 面包卷 | 可能性 |
| 2卷 | 16.67% |
| 3卷 | 44.44% |
| 4卷 | 72.22% |
| 5卷 | 90.74% |
| 6卷 | 98.46% |
掷20个骰子,得到大于100的点数的概率是多少?
我开始使用正态近似来解决这个问题,但超过100个点的概率太低,该方法不够准确。因此,我进行了825万次试验的随机模拟,其中101个点或以上的试验次数为127次。因此,概率约为65,000分之一。
巫师,您能描述一下加州超级乐透(California SuperLotto Plus,4140万分之一)的中奖概率吗?具体来说,是指连续掷出7或11的次数吗?我以前听说过。大多数人无法理解彩票的中奖概率。但是,掷骰子——他们却能理解。
设答案为 n。掷出 7 或 11 的概率为 8/36。求解 n:
(8/36) n = 1/41,400,000
log((8/36) n ) = log(1/41,400,000)
n × log(8/36) = log(1/41,400,000)
n = log(1/41,400,000)/log(8/36)
n = -7.617 / -0.65321
n = 11.6608
所以,超级乐透中奖的概率,相当于连续11.66次掷出7或11的概率。对于那些无法理解“部分投掷”的人,我建议将其理解为连续掷出11到12次的概率。
我们两个工人之间发生了争执。街上有个酒吧,每天摇一次骰子。就是说你必须一次掷五个骰子,而且五个骰子点数必须相同,“就像玩快艇骰子一样”,但是酒吧给你三次机会。但你必须三次都把骰子捡起来。所以问题是,一次掷骰子成功和三次掷骰子成功的可能性分别是多少。谢谢!如果你之前已经回答过这个问题,很抱歉,我找不到了。
一次掷出五条的概率是 6*(1/6) 5 = 1/1,296。这是因为五条有六种不同的形式(一到六),而每次掷出该数字的概率是 (1/6)。掷不出五条的概率是 1-(1/1,296)=1,295/1,296。三次掷不出三条的概率是 (1,295/1,296) 3 =99.77%。因此,三次掷出至少一张五条的概率是 100%-99.77% = 0.23%。
为了获得无偏向的 6 面骰子上每种可能结果中的至少一种,预计需要投掷多少次?
如果某件事的概率是 p,那么平均需要 1/p 次尝试才能第一次发生。显然,第一次掷骰子时你会划掉一个数字。接下来掷出其他五个数字的概率是 5/6。因此,平均需要 1/(5/6)=6/5=1.2 次才能发生这种情况。按照这个推理,预期掷骰子次数为 (6/6)+(6/5)+(6/4)+(6/3)+(6/2)+(6/1) = 14.7。
掷 5 个平衡骰子时,得到总数 12 的经典概率是多少?
希望您满意,我刚刚添加了一个新版块,专门解答类似这样的问题,适用于 1 到 25 个骰子。如五骰子表所示,掷出 12 的概率是 0.039223251028807。
如果反复掷两个骰子,直到发生以下任一事件,那么哪个事件更有可能先发生:
- 掷出的总数为六和八,顺序不限,允许重复。
- 总共掷两次,结果都是七。
有人跟我打赌,6 和 8 会先出现。我答应了,因为 7 是最有可能的数字。然而,我一次又一次地输掉了 2500 美元。这个概率到底有多大?
恐怕你这次下注是赢了。先掷出两个7,再掷出6和8的概率是45.44%。以下是所有可能的结果。第一列是与下注结果相关的掷骰顺序,忽略所有其他结果。
两个七,然后是六和八的赌注
| 相关卷 | 可能性 | 公式 | 结果 |
| 6,8 | 0.142045 | (5/16)*(5/11) | 失去 |
| 8,6 | 0.142045 | (5/16)*(5/11) | 失去 |
| 6,7,8 | 0.077479 | (5/16)*(6/11)*(5/11) | 失去 |
| 7,6,8 | 0.053267 | (6/16)*(5/16)*(5/11) | 失去 |
| 8,7,6 | 0.077479 | (5/16)*(6/11)*(5/11) | 失去 |
| 7,8,6 | 0.053267 | (6/16)*(5/16)*(5/11) | 失去 |
| 7,7 | 0.140625 | (6/16)*(6/16) | 赢 |
| 6,7,7 | 0.092975 | (5/16)*(6/11)*(6/11) | 赢 |
| 8,7,7 | 0.092975 | (5/16)*(6/11)*(6/11) | 赢 |
| 7,6,7 | 0.06392 | (6/16)*(5/16)*(6/11) | 赢 |
| 7,8,7 | 0.06392 | (6/16)*(5/16)*(6/11) | 赢 |
基本上,6 和 8 是更好的选择,因为您可以按任意顺序击中这些数字:6 然后 8,或者 8 然后 6。如果有两个 7,则只有一种顺序,即一个 7 然后另一个 7。
请问两个问题:1)用(6)个六面骰子,一次掷出 6,6,6,6,6,6 的概率是多少?2)用(6)个六面骰子,一次掷出 1,2,3,4,5,6 的概率是多少?谢谢!这太让我头疼了!
六个六的概率是 (1/6) 6 = 1/46656。用六个骰子掷出 1,2,3,4,5,6 的概率是 6 ! /6 6 = 1/64.8
如果掷骰子十次,出现任意给定数字超过一次的概率是多少?
1-(5/6) 10-10 ×(1/6)×(5/6) 9 =51.55%。
在一个名为“逃税与逃税”的游戏中,玩家掷一对骰子。如果掷出的点数为7、11或12,玩家将被审计;如果掷出的点数为其他点数,玩家可以逃税。如果玩家掷出5次这样的骰子,他逃税的概率是多少?
掷出 7、11 或 12 的概率是 (6+2+1)/36 = 9/36 = 1/4。请参阅我关于骰子概率基础的部分,了解我是如何得出这个数字的。掷出其他点数的概率是 3/4。掷 5 次都未掷出 7、11 或 12 的概率是 (3/4) 5 = 23.73%。
你需要掷多少次骰子,才有可能至少掷出 1、2、3、4、5 和 6 一次?有什么办法可以推广到 n 面骰子吗?
虽说你没问,但我先来谈谈平均值。对于一个六面骰子,至少掷出每个面一次的预期次数是 (6/6) + (6/5) + (6/4) + (6/3) + (6/2) + (6/1) = 14.7。对于一个 n 面骰子,预期次数是 (n/n) + (n/(n-1)) + (n/(n-2)) + ... + n。所需掷骰子的中位数是 13。掷出 13 次或更少的概率是 51.4%,掷出 13 次或更多的概率是 56.21%。
我知道你对骰子控制持怀疑态度。我已经练习了三个月的掷骰子和控制投掷了。随机掷了655次,掷出78个7的概率是多少?谢谢你的帮助 :)
对于大量投掷,我们可以使用高斯曲线近似。655次投掷中,预期出现7的次数为655 × (1/6) = 109.1667。方差为655 × (1/6) × (5/6) = 90.9722。标准差为sqr(90.9722) = 9.5379。您的78次投掷结果比预期值低109.1667 − 78 = 31.1667。这相当于(31.1667 - 0.5)/9.5379 = 3.22个标准差。低于预期3.22个或更多标准差的概率为0.000641,即1/1560。我在Excel中使用公式normsdist(-3.22)得出了这个数字。
这是关于掷骰子游戏的骰子控制。您之前讨论过斯坦福·黄实验,其中提到:“赌注的条件是,精准投掷者在500次掷骰子中能否掷出少于79.5个7。在随机游戏中,预期数字是83.33。在500次随机掷骰子中掷出79个或更少7的概率是32.66%……在500次随机掷骰子中掷出74个或更少7的概率是14.41%。”
我对这个赌注的疑问是,14.41% 仍然不是“统计上显著的” [即 p < 0.05],这通常被认为意味着距离平均值大于两个标准差 - 或者事件在系列的任一端随机发生的概率小于*综合* 5%。
在您可以说结果完全随机(即结果具有统计意义)的可能性小于 2.5% 之前,需要在 500 次投掷中投出多少个“7”?
非常感谢,顺便说一句,您的网站绝对是我发现的有关赌博赔率和概率的最佳网站......继续努力!!!
谢谢你的赞美。你不应该说投掷结果非随机的概率是p。应该这样表述:一场随机游戏产生这种结果的概率是p。没人指望500次投掷就能证明或反驳任何事情。我并没有把79.5个7的点数定为79.5,但我怀疑这个点数是否具有统计学意义;相反,我怀疑这是一个双方都会同意下注的点。
2.5% 的显著性水平是与预期值相差 1.96 个标准差。这可以在 Excel 中使用公式 =normsinv(0.025) 计算得出。500 次投掷的标准差为 sqr(500*(1/6)*(5/6)) = 8.333。因此,1.96 个标准差等于 1.96 * 8.333 = 16.333 次,比预期值低。500 次投掷中出现七的预期次数为 500*(1/6) = 83.333。因此,比预期值低 1.96 个标准差等于 83.333 − 16.333 = 67。使用二项分布检验,出现 67 次或更少七的准确概率为 2.627%。
赢得 Yahtzee 需要预计掷多少次?
假设玩家总是持有出现次数最多的数字,则平均值为11.09。下表显示了在8260万次随机模拟试验中,掷骰次数的分布。
骰子实验
| 面包卷 | 发生 | 可能性 |
| 1 | 63908 | 0.00077371 |
| 2 | 977954 | 0.0118396 |
| 3 | 2758635 | 0.0333975 |
| 4 | 4504806 | 0.0545376 |
| 5 | 5776444 | 0.0699327 |
| 6 | 6491538 | 0.0785901 |
| 7 | 6727992 | 0.0814527 |
| 8 | 6601612 | 0.0799227 |
| 9 | 6246388 | 0.0756221 |
| 10 | 5741778 | 0.0695131 |
| 11 | 5174553 | 0.0626459 |
| 12 | 4591986 | 0.0555931 |
| 十三 | 4022755 | 0.0487016 |
| 14 | 3492745 | 0.042285 |
| 15 | 3008766 | 0.0364257 |
| 16 | 2577969 | 0.0312103 |
| 17 | 2193272 | 0.0265529 |
| 18 | 1864107 | 0.0225679 |
| 19 | 1575763 | 0.019077 |
| 20 | 1329971 | 0.0161013 |
| 21 | 1118788 | 0.0135446 |
| 22 | 940519 | 0.0113864 |
| 23 | 791107 | 0.00957757 |
| 24 | 661672 | 0.00801056 |
| 二十五 | 554937 | 0.00671837 |
| 二十六 | 463901 | 0.00561624 |
| 二十七 | 387339 | 0.00468933 |
| 二十八 | 324079 | 0.00392347 |
| 二十九 | 271321 | 0.00328476 |
| 三十 | 225978 | 0.00273581 |
| 31 | 189012 | 0.00228828 |
| 三十二 | 157709 | 0.00190931 |
| 33 | 131845 | 0.00159619 |
| 三十四 | 109592 | 0.00132678 |
| 三十五 | 91327 | 0.00110565 |
| 三十六 | 76216 | 0.00092271 |
| 三十七 | 63433 | 0.00076795 |
| 三十八 | 52786 | 0.00063906 |
| 三十九 | 44122 | 0.00053417 |
| 40 | 36785 | 0.00044534 |
| 41 | 30834 | 0.00037329 |
| 四十二 | 25494 | 0.00030864 |
| 43 | 21170 | 0.0002563 |
| 四十四 | 17767 | 0.0002151 |
| 45 | 14657 | 0.00017745 |
| 46 | 12410 | 0.00015024 |
| 四十七 | 10299 | 0.00012469 |
| 四十八 | 8666 | 0.00010492 |
| 49 | 7355 | 0.00008904 |
| 50 | 5901 | 0.00007144 |
| 51 | 5017 | 0.00006074 |
| 52 | 4227 | 0.00005117 |
| 53 | 3452 | 0.00004179 |
| 54 | 2888 | 0.00003496 |
| 55 | 2470 | 0.0000299 |
| 56 | 2012 | 0.00002436 |
| 57 | 1626 | 0.00001969 |
| 58 | 1391 | 0.00001684 |
| 59 | 1135 | 0.00001374 |
| 60 | 924 | 0.00001119 |
| 61 | 840 | 0.00001017 |
| 62 | 694 | 0.0000084 |
| 63 | 534 | 0.00000646 |
| 64 | 498 | 0.00000603 |
| 65 | 372 | 0.0000045 |
| 66 | 316 | 0.00000383 |
| 67 | 286 | 0.00000346 |
| 68 | 224 | 0.00000271 |
| 69 | 197 | 0.00000238 |
| 70 | 160 | 0.00000194 |
| 71 | 125 | 0.00000151 |
| 72 | 86 | 0.00000104 |
| 73 | 79 | 0.00000096 |
| 74 | 94 | 0.00000114 |
| 75 | 70 | 0.00000085 |
| 76 | 64 | 0.00000077 |
| 77 | 三十八 | 0.00000046 |
| 78 | 四十二 | 0.00000051 |
| 79 | 二十七 | 0.00000033 |
| 80 | 33 | 0.0000004 |
| 81 | 16 | 0.00000019 |
| 82 | 18 | 0.00000022 |
| 83 | 19 | 0.00000023 |
| 84 | 14 | 0.00000017 |
| 85 | 6 | 0.00000007 |
| 86 | 4 | 0.00000005 |
| 87 | 9 | 0.00000011 |
| 88 | 4 | 0.00000005 |
| 89 | 5 | 0.00000006 |
| 90 | 5 | 0.00000006 |
| 91 | 1 | 0.00000001 |
| 92 | 6 | 0.00000007 |
| 93 | 1 | 0.00000001 |
| 94 | 3 | 0.00000004 |
| 95 | 1 | 0.00000001 |
| 96 | 1 | 0.00000001 |
| 97 | 2 | 0.00000002 |
| 102 | 1 | 0.00000001 |
| 全部的 | 82600000 | 1 |
假设一个基于掷骰子的游戏。如果骰子掷出 1,玩家输掉 1 美元,游戏结束。如果骰子掷出其他任何点数,玩家赢取 1 美元。此时,玩家可以选择放弃,也可以选择退出。玩家可以继续游戏,每次下注加倍,直到输掉或退出。最佳策略是什么?
仅从最大化期望值的角度来说,玩家应该永远玩下去。虽然玩家最终输掉的概率是1,但在任何给定的决策点,期望值总是倾向于再次玩下去。这似乎是一个悖论。答案在于,有些事件的概率是1,但仍然可能不会发生。例如,如果你向0到10的数字线投掷飞镖,没有恰好击中π的概率是1,但这仍然有可能发生。
然而,从实际角度来看,存在一个临界点。这是因为金钱带来的幸福感并非与金钱的多少成正比。虽然人们普遍认为金钱越多越幸福,但你越富有,每一美元带来的幸福感就越少。
我认为回答这个问题的一个好方法是运用凯利准则。根据凯利准则,玩家在做每一个决定时都应该以最大化下注后资金的预期对数为目标。简而言之(我省略了很多数学运算),玩家应该不断加倍,直到下注金额超过其总财富的 96.5948%。财富应该定义为赢得的金额加上玩家在第一次下注前拥有的资金之和。例如,如果玩家的起始资金为 100,000 美元,他应该不断加倍,直到赢得 4,194,304 美元。此时,玩家的总财富将达到 4,294,304 美元。他将被要求下注 4,194,304/4,294,304 = 其总财富的 96.67%,这大于 96.5948% 的停止点,所以他应该退出。
玩家 A 和 B 掷一对骰子。如果玩家 A 在 B 掷出 7 之前掷出 6,则 A 获胜;如果 B 在 A 掷出 6 之前掷出 7,则 B 获胜。如果由 A 先掷,则说明 A 获胜的概率为 30/61。
假设这个问题的答案为 p。掷出总点数 6 的概率是 5/36,掷出总点数 7 的概率是 6/36。如果您不明白为什么,请参阅我关于骰子概率基础的部分。我们可以将 p 定义为:
p = Prob(第一次掷出 6) + Prob(第一次掷出未出现 6)*Prob(第二次掷出未出现 7)*p。
这是因为,如果前两次掷骰子后没有一个玩家获胜,游戏就会回到原始状态,玩家 A 获胜的概率保持不变。
因此,我们有:
p = (5/36) + (31/36)×(30/36)×p
p = 5/36 + (930/1296)×p
p * (1-(930/1296)) = 5/36。
p * (366/1296) = 5/36
p = (5/36)×(1296/366) = 30/61。
掷 n 个六面且点数相同的骰子有多少种方法?如上所述,骰子点数相同,因此,例如,如果掷 5 个骰子,1-1-3-5-6 和 1-6-5-1-3 会被视为相同的结果。如果掷 2 个骰子,很容易确定答案是 21,但我找不到一个优雅且通用的解决方案。
答案可以表示为 combin(n+5,n) = (n+5)!/(120×n!)。以下是 1 到 20 个骰子的答案。
非唯一骰子组合
| 骰子 | 组合 |
| 1 | 6 |
| 2 | 21 |
| 3 | 56 |
| 4 | 126 |
| 5 | 252 |
| 6 | 462 |
| 7 | 792 |
| 8 | 1287 |
| 9 | 2002 |
| 10 | 3003 |
| 11 | 4368 |
| 12 | 6188 |
| 十三 | 8568 |
| 14 | 11628 |
| 15 | 15504 |
| 16 | 20349 |
| 17 | 26334 |
| 18 | 33649 |
| 19 | 42504 |
| 20 | 53130 |
| 21 | 65780 |
| 22 | 80730 |
| 23 | 98280 |
感谢《应用组合学》的作者艾伦·塔克 (Alan Tucker)。
你能计算一下掷骰子时两个数字接连出现的概率吗?也就是说,连续出现两个4、两个6或两个7的概率是多少?我知道过去无法预测未来,但有没有办法计算出7/36 x 7/36连续出现的概率?希望你理解得通。
当然。那就是 Pr(2) 2 + Pr(3) 2 + ... + Pr(12) 2 = (1/36) 2 + (2/36) 2 + (3/36) 2 + (4/36) 2 + (5/36) 2 + (6/36) 2 + (5/36) 2 + (4/36) 2 + (3/36) 2 + (2/36) 2 + (1/36) 2 = 11.27%。
在连续 180 次掷骰子中,我预计会看到以下结果多少次:
连续两个七?
连续三个七?
连续四个七?
感谢您的时间:-)。
我想不出任何有用的理由来了解这些信息,但我经常被问到这种问题,所以我会迁就你。
从第一次掷骰开始,或从最后一次掷骰结束,得到一个指定的7的序列会稍微容易一些,因为这个序列有界于某一侧。具体来说,从第一次掷骰开始,或从最后一次掷骰结束,得到s个7的序列的概率是(1/6) s × (5/6)。5/6项是因为你必须在序列的开口端得到一个非7的点数。
在序列中间任意一点开始 s 个 7 的序列的概率是 (1/6) s × (5/6) 2 。我们将 5/6 取平方,因为玩家必须在序列的两端都拿到非 7 的点数。
如果掷出 r 次,则内侧序列有 2 个位置,连续 n 个 7 有 rn-1 个位置。将这些公式代入表格中,即可得出连续 7 的预期次数,范围从 1 到 10。“内侧”列为 2*(5/6)*(1/6) r ,“外侧”列为 (179-r)*(5/6) 2 *(1/6) r ,其中 r 是连续 7 的个数。因此,我们预期连续出现两个 7 的概率为 3.46,连续出现三个 7 的概率为 0.57,连续出现四个 7 的概率为 0.10。
180 次投掷中预期出现 7 的次数
| 跑步 | 里面 | 外部 | 全部的 |
| 1 | 0.277778 | 20.601852 | 20.87963 |
| 2 | 0.046296 | 3.414352 | 3.460648 |
| 3 | 0.007716 | 0.565844 | 0.57356 |
| 4 | 0.001286 | 0.093771 | 0.095057 |
| 5 | 0.000214 | 0.015539 | 0.015754 |
| 6 | 0.000036 | 0.002575 | 0.002611 |
| 7 | 0.000006 | 0.000427 | 0.000433 |
| 8 | 0.000001 | 0.000071 | 0.000072 |
| 9 | 0 | 0.000012 | 0.000012 |
| 10 | 0 | 0.000002 | 0.000002 |
掷两个骰子,直到总数为 12 或连续两次总数为 7。首先掷出 12 的概率是多少?
答案和解决方案可以在我的配套网站mathproblems.info问题 201 上找到。
我是个桌游玩家,之前和朋友们讨论过非立方体柏拉图式立体骰子(如果你够酷的话,那就意味着 d4、d8、d12 和 d20)。他们说只有这些骰子才能真正公平。我则认为,制造出公平的骰子实在太难了。而且,它们只能玩一些类似掷骰子的游戏,由于额外结果太多,玩起来会变得过于繁琐。有哪家赌场推出过使用非传统六面骰子的游戏吗?
|
如果你只考虑正多边形,并希望每个面都有相同的概率,那么你就只能考虑柏拉图立体。但是,如果你能取消对正多边形的要求,那么你也可以添加13个加泰罗尼亚立体。
回答你的另一个问题,没有,我从未在赌场里见过任何游戏使用除立方体以外的骰子。大约十年前,我在大西洋城的一个游戏展上看到过一款游戏演示,我记得它用的是菱形三十面体(加泰罗尼亚立体的一种),但我觉得它从未出现在赌场里。我每年都会在全球游戏博览会上看到一款游戏使用陀螺(类似陀螺),但可惜的是,我也没在赌场里见过。
如果我掷三个六面骰子,掷出顺子的概率是多少?掷出三条的概率是多少?
掷三个骰子有 6 3 = 216 种方法。其中六种组合会得到三条(1-1-1 到 6-6-6)。因此,得到三条的概率为 6/216 = 1/36。顺子有四种可能的组合(1-2-3 到 4-5-6)。同样,将三个骰子排列成顺子也有 3!=6 种方法。因此,有 4*6=24 种顺子组合。因此,得到顺子的概率为 24/216 = 1/9。
掷四个六面骰子,减去最小点数(即 4d6-L)后,平均点数是多少?标准差是多少?
下表显示了从 3 到 18 的所有可能总数的组合数。
4d6-L 中的组合
| 结果 | 组合 |
| 3 | 1 |
| 4 | 4 |
| 5 | 10 |
| 6 | 21 |
| 7 | 三十八 |
| 8 | 62 |
| 9 | 91 |
| 10 | 122 |
| 11 | 148 |
| 12 | 167 |
| 十三 | 172 |
| 14 | 160 |
| 15 | 131 |
| 16 | 94 |
| 17 | 54 |
| 18 | 21 |
| 全部的 | 1296 |
平均结果为 12.2446,标准差为 2.8468。
我的问题是基于骰子概率的。我知道掷出 7 有六种方法,掷出 12 有一种方法,但是掷出六个 7 而不是一个 12 的概率是多少?它们是等价的吗?如果不是,那么应该在等式中添加多少个 12 才能使结果为等价?
掷出 7 的概率是 1/6,掷出 12 的概率是 1/36。假设掷出的点数为 7 或 12,掷出 7 的概率为 (1/6)/((1/6)+(1/36)) = 6/7。因此,前六次掷出 6 或 12 时,每次都是 6 的概率为 (6/7) 6 = 39.66%。
如果你把问题改写成在掷出12之前掷出五个6的概率是多少,那么答案是(6/7) 5 = 46.27%。如果掷出四次,答案是(6/7) 4 = 53.98%。所以,在掷出12之前,不存在任何恰好50/50的7。如果你想赌一把,建议你要么在掷出12之前掷出四个7,要么在掷出五个7之前掷出一个12。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
有没有简单的方法来计算用 d 个 6 面骰子掷出总数为 t 的概率?
这里有一个实用技巧,由英国萨默塞特郡的罗伯特·古德汉(Robert Goodhand)提供。首先,在一行中放入六个“1”,两边分别围上五个“0”,如下所示:
单骰子概率
| 骰子总数 | 1 | 2 | 3 | 4 | 5 | 6 | ||||||||||
| 一模一样 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
这表示用一个骰子掷出 1 到 6 的组合数。我知道,这很明显。不过,请听我说完。如果是两个骰子,在底部添加一行,每个格子取上一行与其左侧五个格子之和。然后,如果您想继续,在右侧再添加五个虚拟零。这表示掷出总数为 2 到 12 的组合数。
两个骰子的概率
| 骰子总数 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||||||||||
| 一模一样 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 两个骰子 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 0 | 0 | 0 | 0 |
如果掷三个骰子,只需重复即可。这将代表3到18的组合数。
要计算任意给定点数的概率,用该点数的组合数除以组合总数。如果是三枚骰子,其总和为 216,也可以很容易地计算为 6 的3 次方。例如,三枚骰子掷出总点数 13 的概率为 21/216 = 9.72%。
所以对于 d 号骰子,你需要从 1 号骰子到 d-1 号骰子依次计算。这在任何电子表格中都很容易完成。
需要掷多少次骰子才能有 50/50 的概率掷出至少一个 12 点?
这是概率论史上的一个经典问题。很多人错误地认为答案是 18,因为掷出 12 的概率是 1/36,而 18×(1/36)=50%。然而,按照这个逻辑,掷 36 次得到 12 的概率应该是 100%,这显然不是。以下是正确答案。设 r 为掷骰次数。掷出非 12 的概率是 35/36。掷 r 次骰子中没有掷出 12 的概率是 (35/36) r 。因此,我们需要用以下公式解出 r:
(35/36) r = 0.5
对数(35/36) r = 对数(0.5)
r × log(35/36) = log(0.5)
r = log(0.5)/log(35/36)
r = 24.6051
所以没有一个整数答案。24次掷骰子中掷出12的概率是1-(35/36) 24 = 49.14%。25次掷骰子中掷出12的概率是1-(35/36) 25 = 50.55%。
如果你想押注,比如说你能在25轮中掷出12点,或者其他人在24轮中掷不出。无论哪种情况,你都能在均等投注中占据优势。
在骰子战争中,给定进攻和防守骰子的数量,成功的概率是多少?作为进攻方,哪个比例的预期收益最大?
对于不熟悉游戏的人来说,进攻方和防守方都会根据战斗中各自拥有的军队数量,掷1到8个骰子。点数较高的一方获胜。如果平局,则防守方获胜。如果进攻方失败,他仍然可以在发起进攻的领土上保留一支军队。因此,他必须至少拥有两支军队才能进攻,这样如果他获胜,一支军队可以占领被征服的领土,另一支军队可以留在原地。
下表显示了根据所有 64 种骰子组合,攻击者获胜的概率。
攻击者获胜的概率
| 攻击者 | 后卫 | |||||||
|---|---|---|---|---|---|---|---|---|
| 第1军 | 2支军队 | 3支军队 | 4支军队 | 5支军队 | 6支军队 | 7支军队 | 8支军队 | |
| 2 | 0.837963 | 0.443673 | 0.152006 | 0.035880 | 0.006105 | 0.000766 | 0.000071 | 0.000005 |
| 3 | 0.972994 | 0.778549 | 0.453575 | 0.191701 | 0.060713 | 0.014879 | 0.002890 | 0.000452 |
| 4 | 0.997299 | 0.939236 | 0.742831 | 0.459528 | 0.220442 | 0.083423 | 0.025450 | 0.006379 |
| 5 | 0.999850 | 0.987940 | 0.909347 | 0.718078 | 0.463654 | 0.242449 | 0.103626 | 0.036742 |
| 6 | 0.999996 | 0.998217 | 0.975300 | 0.883953 | 0.699616 | 0.466731 | 0.259984 | 0.121507 |
| 7 | 1.000000 | 0.999801 | 0.994663 | 0.961536 | 0.862377 | 0.685165 | 0.469139 | 0.274376 |
| 8 | 1.000000 | 0.999983 | 0.999069 | 0.989534 | 0.947731 | 0.843874 | 0.673456 | 0.471091 |
下表显示了攻击者的预期收益,定义为pr(攻击者获胜)*(防御者骰子)+pr(防御者获胜)*(攻击者骰子-1)。结果显示,最大的预期收益是以8点进攻,对手以5点进攻。
攻击者获胜的净收益
| 攻击者 | 后卫 | |||||||
|---|---|---|---|---|---|---|---|---|
| 第1军 | 2支军队 | 3支军队 | 4支军队 | 5支军队 | 6支军队 | 7支军队 | 8支军队 | |
| 2 | 0.675926 | 0.331019 | -0.391976 | -0.820600 | -0.963370 | -0.994638 | -0.999432 | -0.999955 |
| 3 | 0.918982 | 1.114196 | 0.267875 | -0.849794 | -1.575009 | -1.880968 | -1.973990 | -1.995480 |
| 4 | 0.989196 | 1.696180 | 1.456986 | 0.216696 | -1.236464 | -2.249193 | -2.745500 | -2.929831 |
| 5 | 0.999250 | 1.927640 | 2.365429 | 1.744624 | 0.172886 | -1.575510 | -2.860114 | -3.559096 |
| 6 | 0.999976 | 1.987519 | 2.802400 | 2.955577 | 1.996160 | 0.134041 | -1.880192 | -3.420409 |
| 7 | 1.000000 | 1.998408 | 2.951967 | 3.615360 | 3.486147 | 2.221980 | 0.098807 | -2.158736 |
| 8 | 1.000000 | 1.999847 | 2.990690 | 3.884874 | 4.372772 | 3.970362 | 2.428384 | 0.066365 |
掷骰子 n 次,形成 Yahtzee 的概率是多少?
为了方便其他读者理解,Yahtzee 指的是用五个骰子掷出五条的骰子。在 Yahtzee 游戏中,玩家可以保留任意一个骰子,然后重新掷出剩余的骰子。最多可以掷三次。
如果玩家愿意,可以重新掷出之前持有的骰子。例如,如果玩家第一次掷出的骰子是 3-3-4-5-6,他手中持有的是 3,第二次掷出的骰子是 3-3-5-5-5,那么他可以保留 5,并在第三次掷出的骰子上重新掷出 3。
下表列出了1至20次投掷中,相同面数的骰子的最大数量。该表显示,三次投掷中赢得Yahtzee的概率约为4.6%。
骰子概率
| 面包卷 | 同面最大骰子 | ||||
|---|---|---|---|---|---|
| 一 | 二 | 三 | 四 | 五 | |
| 1 | 0.092593 | 0.694444 | 0.192901 | 0.019290 | 0.000772 |
| 2 | 0.008573 | 0.450103 | 0.409022 | 0.119670 | 0.012631 |
| 3 | 0.000794 | 0.256011 | 0.452402 | 0.244765 | 0.046029 |
| 4 | 0.000074 | 0.142780 | 0.409140 | 0.347432 | 0.100575 |
| 5 | 0.000007 | 0.079373 | 0.337020 | 0.413093 | 0.170507 |
| 6 | 0.000001 | 0.044101 | 0.263441 | 0.443373 | 0.249085 |
| 7 | 0.000000 | 0.024501 | 0.199279 | 0.445718 | 0.330502 |
| 8 | 0.000000 | 0.013612 | 0.147462 | 0.428488 | 0.410438 |
| 9 | 0.000000 | 0.007562 | 0.107446 | 0.398981 | 0.486011 |
| 10 | 0.000000 | 0.004201 | 0.077416 | 0.362855 | 0.555528 |
| 11 | 0.000000 | 0.002334 | 0.055317 | 0.324175 | 0.618174 |
| 12 | 0.000000 | 0.001297 | 0.039279 | 0.285674 | 0.673750 |
| 十三 | 0.000000 | 0.000720 | 0.027757 | 0.249063 | 0.722460 |
| 14 | 0.000000 | 0.000400 | 0.019543 | 0.215313 | 0.764744 |
| 15 | 0.000000 | 0.000222 | 0.013720 | 0.184883 | 0.801175 |
| 16 | 0.000000 | 0.000124 | 0.009610 | 0.157896 | 0.832371 |
| 17 | 0.000000 | 0.000069 | 0.006719 | 0.134258 | 0.858954 |
| 18 | 0.000000 | 0.000038 | 0.004692 | 0.113753 | 0.881517 |
| 19 | 0.000000 | 0.000021 | 0.003272 | 0.096100 | 0.900607 |
| 20 | 0.000000 | 0.000012 | 0.002280 | 0.080994 | 0.916714 |
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
我想知道掷一对骰子时,哪个点数会更大——奇数还是偶数?
答案是50/50。无论掷多少个骰子,结果都是50/50,而不仅仅是两个。
有点跑题了,但我一直觉得奇偶组合下注是替代掷骰子游戏中令人畏惧的6/8大注的好方法。为了让赌场更有优势,以下是我建议的赔率表和分析。
奇数投注
| 事件 | 支付 | 组合 | 可能性 | 返回 |
|---|---|---|---|---|
| 3 或 11 | 1.5 | 4 | 0.111111 | 0.166667 |
| 5或9 | 1 | 8 | 0.222222 | 0.222222 |
| 7 | 0.5 | 6 | 0.166667 | 0.083333 |
| 甚至 | -1 | 18 | 0.500000 | -0.500000 |
| 全部的 | 三十六 | 1.000000 | -0.027778 |
均等投注
| 事件 | 支付 | 组合 | 可能性 | 返回 |
|---|---|---|---|---|
| 2 或 12 | 3 | 2 | 0.055556 | 0.166667 |
| 4 或 10 | 1 | 6 | 0.166667 | 0.166667 |
| 6或8 | 0.5 | 10 | 0.277778 | 0.138889 |
| 奇怪的 | -1 | 18 | 0.500000 | -0.500000 |
| 全部的 | 三十六 | 1.000000 | -0.027778 |
请注意,我对该出版物主张所有权利。
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
在 Hot Roll 奖励中,玩家根据两个骰子的总点数赢得以下数量的硬币:
- 2 或 12:1000
- 3或11:600
- 4或10:400
- 5或9:300
- 6或8:200
他一直掷到总数为7,奖励结束。如果第一次掷出7,他将获得700枚硬币的安慰奖。每次奖励平均能赢得多少枚硬币?
平均掷骰次数与奖励结束事件的概率相反,后者的概率为1/6,因此玩家平均掷骰六次。然而,最后一次掷骰次数将是七次,因此平均每次奖励有五次获胜。
接下来,假设不是七,以下是每个总数的概率:
- 2 或 12:1/30
- 3或11:2/30
- 4或10:3/30
- 5或9:4/30
- 6或8:5/30
因此,假设没有七点,每次掷骰子的平均胜利是 2*[(1/30)*1000 + (2/30)*600 + (3/30)*400 + (4/30)*300 + (5/30)*200] = 373.33。
安慰奖的金额为(1/6)*700=116.67。
因此,平均奖金赢额为 116.67 + 5×373.33 = 1983.33。
如果玩家轮流掷骰子,并且只有掷骰子的玩家才能根据掷出的点数前进,那么“询问巫师”专栏第 179 栏中的骰子问题的答案是什么?
这是第 179 栏中提出的原始问题:如果反复掷两个骰子,直到发生以下任一事件,那么哪个事件更有可能先发生:
- 掷出的总数为六和八,顺序不限,允许重复。
- 总共掷两次,结果都是七。
你的改动是,同一个掷骰子不能同时帮助两个玩家。相反,他们轮流掷骰子,并且只有掷骰子的玩家可以使用该掷骰子。
答案取决于谁先掷骰子。如果先掷出需要六和八的玩家,那么他获胜的概率是 57.487294%。如果先掷出需要两张七的玩家,那么先掷出需要六和八的玩家获胜的概率是 52.671614%。我用一个简单的马尔可夫链过程解决了这个问题。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
假设你有12个六面骰子。你掷它们,然后可以把任何你想弃掉的骰子放在一边。然后你重新掷剩下的骰子。两次掷出12点的概率是多少?
初始掷骰结果有 58 种不同的序列。我识别每种序列的方法是:先计算骰子面数,然后计算骰子面数第二的骰子总数,以此类推。例如,掷出 3,3,3,3,6,6,6,5,5,2 的概率表示为 4-3-2-1。下表列出了每种序列的组合数、掷出该序列的概率、第二次掷出相同点数 12 的概率以及两者的乘积。对于第二次掷出的概率,我假设玩家持有初始掷骰结果最大的骰子。右下角单元格显示的总概率为 0.0000037953,相当于 263,486 分之一。
12 骰子问题
| 顺序 | 组合 | 可能性 顺序 | 条件 可能性 | 全部的 可能性 |
|---|---|---|---|---|
| 12-0-0-0-0-0 | 6 | 0.0000000028 | 1.0000000000 | 0.0000000028 |
| 11-1-0-0-0-0 | 360 | 0.0000001654 | 0.1666666667 | 0.0000000276 |
| 10-2-0-0-0-0 | 1,980 | 0.0000009096 | 0.0277777778 | 0.0000000253 |
| 10-1-1-0-0-0 | 7,920 | 0.0000036384 | 0.0277777778 | 0.0000001011 |
| 9-3-0-0-0-0 | 6,600 | 0.0000030320 | 0.0046296296 | 0.0000000140 |
| 9-2-1-0-0-0 | 79,200 | 0.0000363840 | 0.0046296296 | 0.0000001684 |
| 9-1-1-1-0-0 | 79,200 | 0.0000363840 | 0.0046296296 | 0.0000001684 |
| 8-4-0-0-0-0 | 14,850 | 0.0000068220 | 0.0007716049 | 0.0000000053 |
| 8-3-1-0-0-0 | 237,600 | 0.0001091519 | 0.0007716049 | 0.0000000842 |
| 8-2-2-0-0-0 | 178,200 | 0.0000818639 | 0.0007716049 | 0.0000000632 |
| 8-2-1-1-0-0 | 1,069,200 | 0.0004911837 | 0.0007716049 | 0.0000003790 |
| 8-1-1-1-1-0 | 356,400 | 0.0001637279 | 0.0007716049 | 0.0000001263 |
| 7-5-0-0-0-0 | 23,760 | 0.0000109152 | 0.0001286008 | 0.0000000014 |
| 7-4-1-0-0-0 | 475,200 | 0.0002183039 | 0.0001286008 | 0.0000000281 |
| 7-3-2-0-0-0 | 950,400 | 0.0004366077 | 0.0001286008 | 0.0000000561 |
| 7-3-1-1-0-0 | 2,851,200 | 0.0013098232 | 0.0001286008 | 0.0000001684 |
| 7-2-2-1-0-0 | 4,276,800 | 0.0019647348 | 0.0001286008 | 0.0000002527 |
| 7-2-1-1-1-0 | 5,702,400 | 0.0026196464 | 0.0001286008 | 0.0000003369 |
| 7-1-1-1-1-1 | 570,240 | 0.0002619646 | 0.0001286008 | 0.0000000337 |
| 6-6-0-0-0-0 | 13,860 | 0.0000063672 | 0.0000214335 | 0.0000000001 |
| 6-5-1-0-0-0 | 665,280 | 0.0003056254 | 0.0000214335 | 0.0000000066 |
| 6-4-2-0-0-0 | 1,663,200 | 0.0007640635 | 0.0000214335 | 0.0000000164 |
| 6-4-1-1-0-0 | 4,989,600 | 0.0022921906 | 0.0000214335 | 0.0000000491 |
| 6-3-3-0-0-0 | 1,108,800 | 0.0005093757 | 0.0000214335 | 0.0000000109 |
| 6-3-2-1-0-0 | 19,958,400 | 0.0091687624 | 0.0000214335 | 0.0000001965 |
| 6-3-1-1-1-0 | 13,305,600 | 0.0061125083 | 0.0000214335 | 0.0000001310 |
| 6-2-2-2-0-0 | 4,989,600 | 0.0022921906 | 0.0000214335 | 0.0000000491 |
| 6-2-2-1-1-0 | 29,937,600 | 0.0137531436 | 0.0000214335 | 0.0000002948 |
| 6-2-1-1-1-1 | 9,979,200 | 0.0045843812 | 0.0000214335 | 0.0000000983 |
| 5-5-2-0-0-0 | 997,920 | 0.0004584381 | 0.0000035722 | 0.0000000016 |
| 5-5-1-1-0-0 | 2,993,760 | 0.0013753144 | 0.0000035722 | 0.0000000049 |
| 5-4-3-0-0-0 | 3,326,400 | 0.0015281271 | 0.0000035722 | 0.0000000055 |
| 5-4-2-1-0-0 | 29,937,600 | 0.0137531436 | 0.0000035722 | 0.0000000491 |
| 5-4-1-1-1-0 | 19,958,400 | 0.0091687624 | 0.0000035722 | 0.0000000328 |
| 5-3-3-1-0-0 | 19,958,400 | 0.0091687624 | 0.0000035722 | 0.0000000328 |
| 5-3-2-2-0-0 | 29,937,600 | 0.0137531436 | 0.0000035722 | 0.0000000491 |
| 5-3-2-1-1-0 | 119,750,400 | 0.0550125743 | 0.0000035722 | 0.0000001965 |
| 5-3-1-1-1-1 | 19,958,400 | 0.0091687624 | 0.0000035722 | 0.0000000328 |
| 5-2-2-2-1- | 59,875,200 | 0.0275062872 | 0.0000035722 | 0.0000000983 |
| 5-2-2-1-1-1 | 59,875,200 | 0.0275062872 | 0.0000035722 | 0.0000000983 |
| 4-4-4-0-0-0 | 693,000 | 0.0003183598 | 0.0000005954 | 0.0000000002 |
| 4-4-3-1-0-0 | 24,948,000 | 0.0114609530 | 0.0000005954 | 0.0000000068 |
| 4-4-2-2-0-0 | 18,711,000 | 0.0085957147 | 0.0000005954 | 0.0000000051 |
| 4-4-2-1-1-0 | 74,844,000 | 0.0343828589 | 0.0000005954 | 0.0000000205 |
| 4-4-1-1-1-1 | 12,474,000 | 0.0057304765 | 0.0000005954 | 0.0000000034 |
| 4-3-3-2-0-0 | 49,896,000 | 0.0229219060 | 0.0000005954 | 0.0000000136 |
| 4-3-3-1-1-0 | 99,792,000 | 0.0458438119 | 0.0000005954 | 0.0000000273 |
| 4-3-2-2-1-0 | 299,376,000 | 0.1375314358 | 0.0000005954 | 0.0000000819 |
| 4-3-2-1-1-1 | 199,584,000 | 0.0916876238 | 0.0000005954 | 0.0000000546 |
| 4-2-2-2-2-0 | 37,422,000 | 0.0171914295 | 0.0000005954 | 0.0000000102 |
| 4-2-2-2-1-1 | 149,688,000 | 0.0687657179 | 0.0000005954 | 0.0000000409 |
| 3-3-3-3-0-0 | 5,544,000 | 0.0025468784 | 0.0000000992 | 0.0000000003 |
| 3-3-3-2-1-0 | 133,056,000 | 0.0611250826 | 0.0000000992 | 0.0000000061 |
| 3-3-3-1-1-1 | 44,352,000 | 0.0203750275 | 0.0000000992 | 0.0000000020 |
| 3-3-2-2-2-0 | 99,792,000 | 0.0458438119 | 0.0000000992 | 0.0000000045 |
| 3-3-2-2-1-1 | 299,376,000 | 0.1375314358 | 0.0000000992 | 0.0000000136 |
| 3-2-2-2-2-1 | 149,688,000 | 0.0687657179 | 0.0000000992 | 0.0000000068 |
| 2-2-2-2-2-2 | 7,484,400 | 0.0034382859 | 0.0000000165 | 0.0000000001 |
| 全部的 | 2,176,782,336 | 1.0000000000 | 0.0000037953 |
平均而言,需要掷多少次公平的骰子才能使每个面至少掷出两次?
点击下面的按钮获取答案。
这是我的解决方案。(PDF)
我在Wizard of Vegas论坛上提出并讨论了这个问题。
假设掷一个公平的六面骰子,直到出现1、2、3或6。如果1、2或3是这些游戏结束数字中第一个出现的,那么您什么也赢不了。如果6是这些游戏结束数字中第一个出现的,那么您每次掷骰子都会赢得1美元。这场比赛的平均赢利是多少?
单击下面的按钮,查看几个可能对您有帮助的无穷级数公式。
[剧透=提示]
提示 1:对 n 求 i = 0 到 ∞ 的和i = 1 / (1-n)
提示 2:i = 0 到 ∞ 的 i × n 之和i = n / (1-n) 2
[/spoiler]点击下面的按钮获取答案。
单击下面的按钮获取解决方案。
[剧透=解决方案]
假设掷一个公平的六面骰子,直到出现1、2、3或6。如果1、2或3是这些游戏结束数字中第一个出现的,那么您什么也赢不了。如果6是这些游戏结束数字中第一个出现的,那么您每次掷骰子都会赢得1美元。这场比赛的平均赢利是多少?
提示 1:对 n 求 i = 0 到 ∞ 的和i = 1 / (1-n)
提示 2:i = 0 到 ∞ 的 i × n 之和i = n / (1-n) 2
预期赢利可以表示为 i = 0 到 ∞ 的 (1 + i) * (1/3) i * (1/6) 之和。=
(1/6)* (1/3) i 的 i = 0 到 ∞ 的总和+ (1/6)* (i * (1/3) i ) 的 i = 0 到 ∞ 的总和。
让我们逐一评估一下。
i = 0 到 ∞ 的和,其中 (1/3) i =
1 / (1 - (1/3)) =
1 / (2/3) =
3/2
i = 0 到 ∞ 的和 (i * (1/3) i ) =
(1/3)/(1-(1/3)) 2 =
(1/3)/(4/9)=
(1/3)*(9/4)=
3/4
综合起来,答案是
(1/6)*(3/2)+(1/6)*(3/4)=
(1/4)+(1/8)=
3/8
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
掷一个公平的骰子,每个面至少掷出两次,预期掷骰子的次数是多少?
[剧透=解决方案]
虽然这个问题可以用冗长乏味的马尔可夫链来解决,但我更喜欢用积分法。我在我的Fire Bet和Bonus Craps页面中解释了如何使用这种方法。
想象一下,重大事件不再由一次掷骰子决定,而是被视为一个时间瞬间。假设事件之间的时间间隔具有无记忆性,平均间隔为一个时间单位。换句话说,事件之间的时间间隔服从均值为1的指数分布。这对于裁决赌注来说无关紧要,因为事件仍然是一次一个地发生的。
根据泊松分布,在 x 个单位时间内,骰子任意一面掷出次数为零的概率为 exp(-x/6)*(x/6) 0 /0! = exp(-x/6)。泊松分布还表示,任意一面掷出恰好一次的概率为 exp(-x/6)*(x/6) 1 /1! = exp(-x/6) * (x/6)。因此,任意一面在 x 个单位时间内掷出两次或两次以上概率为 1 - exp(-x/6)*(1 + (x/6))。六面掷出至少两次的概率为 (1 - exp(-x/6)*(1 + (x/6))) 6。至少有一面未掷出至少两次的概率等于:
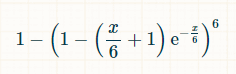
我们需要将其与所有时间结合起来,以找出平均需要多长时间才能实现预期目标。
幸运的是,我们此时可以使用积分计算器。对于链接中的那个,在“计算积分”后面的文本框中输入 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = apx. 24.1338692,并在自定义下将积分的边界设置为 0 到 ∞。
答案是 390968681 / 16200000 = 约 24.13386919753086
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
你先用一个公平的六面骰子掷六次,并记录每次掷出的结果。然后,你把这些数字写在另一个没有标签的公平骰子的六个面上。例如,如果你掷出的六次结果是3、5、3、6、1和2,那么你的第二个骰子上就不会出现4,而是会出现两个3。
接下来,你把第二个骰子掷六次。把这六个数字写在另一个公平骰子上,然后继续这个过程,用前一个骰子生成一个新的骰子。
最终,你会得到一个六个面点数都相同的骰子。为了达到这个状态,从一个骰子转换到另一个骰子的平均次数是多少(或者总掷骰数除以6)?
[剧透=解决方案]
为了避免混淆,我们用字母而不是数字来标记初始骰子。我们用字母标记每个可能的骰子状态。例如,AAABBC 表示三个同种字母,两个同种字母,一个同种字母。初始状态显然是 ABCDEF。
令 E(ABCDEF) 为从状态 ABCDEF 开始的预期掷骰次数。
E(ABCDEF) = 1 + [180 × E(AAAAAB) + 450 × E(AAAABB) + 300 × E(AAABBB) + 1800 × E(AAAABC) + 7200 × E(AAABBC) + 1800 × E(AABBCC) + 7200 × E(AAABCD) + 16200 × E(AABBCD) + 10800 × E(AABCDE) + 720 × E(ABCDEF)]/46656基于从一个状态到另一个状态的组合数量,下面的转换矩阵展示了从每个初始状态(左列)到每个新状态的转换方式数量。顺便说一下,这花了几个小时才构建好。
过渡矩阵A
| 状态 前 | 啊啊啊啊啊 | AAAAB | AAAABB | AAABBB | AAAABC | AAABBC | 美国商务部商务合作委员会 | AAAABCD | ABCD | ABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|---|
| AAAAB | 15,626 | 18,780 | 9,750 | 2,500 | - | - | - | - | - | - | - |
| AAAABB | 4,160 | 13,056 | 19,200 | 10,240 | - | - | - | - | - | - | - |
| AAABBB | 1,458 | 8,748 | 21,870 | 14,580 | - | - | - | - | - | - | - |
| AAAABC | 4,098 | 12,348 | 8,190 | 2,580 | 7,920 | 10,080 | 1,440 | - | - | - | - |
| AAABBC | 794 | 5,172 | 8,670 | 5,020 | 6,480 | 17,280 | 3,240 | - | - | - | - |
| 美国商务部商务合作委员会 | 192 | 2,304 | 5,760 | 3,840 | 5,760 | 23,040 | 5,760 | - | - | - | - |
| AAAABCD | 732 | 4,464 | 4,140 | 1,680 | 7,920 | 14,400 | 2,520 | 4,320 | 6,480 | - | - |
| ABCD | 130 | 1,596 | 3,150 | 1,940 | 5,280 | 16,800 | 3,600 | 4,800 | 9,360 | - | - |
| ABCDE | 68 | 888 | 1,380 | 760 | 3,960 | 11,520 | 2,520 | 7,200 | 14,040 | 4,320 | - |
| ABCDEF | 6 | 180 | 450 | 300 | 1,800 | 7,200 | 1,800 | 7,200 | 16,200 | 10,800 | 720 |
我不会长篇大论地讲解矩阵代数,只是假设矩阵 B 如下:
矩阵B
| 状态 前 | AAAAB | AAAABB | AAABBB | AAAABC | AAABBC | 美国商务部商务合作委员会 | AAAABCD | ABCD | ABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|
| AAAAB | -27876 | 9750 | 2500 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABB | 13056 | -27456 | 10240 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAABBB | 8748 | 21870 | -32076 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABC | 12348 | 8190 | 2580 | -38736 | 10080 | 1440 | 0 | 0 | 0 | -46656 |
| AAABBC | 5172 | 8670 | 5020 | 6480 | -29376 | 3240 | 0 | 0 | 0 | -46656 |
| 美国商务部商务合作委员会 | 2304 | 5760 | 3840 | 5760 | 23040 | -40896 | 0 | 0 | 0 | -46656 |
| AAAABCD | 4464 | 4140 | 1680 | 7920 | 14400 | 2520 | -42336 | 6480 | 0 | -46656 |
| ABCD | 1596 | 3150 | 1940 | 5280 | 16800 | 3600 | 4800 | -37296 | 0 | -46656 |
| ABCDE | 888 | 1380 | 760 | 3960 | 11520 | 2520 | 7200 | 14040 | -42336 | -46656 |
| ABCDEF | 180 | 450 | 300 | 1800 | 7200 | 1800 | 7200 | 16200 | 10800 | -46656 |
答案是矩阵 B 的行列式与矩阵 A 的行列式之比:
确定(A)= 1,461,067,501,120,670,000,000,000,000,000,000,000,000,000,000,000
确定(B)= 14,108,055,348,203,100,000,000,000,000,000,000,000,000,000,000,000
Determ(B) / Determ(A) = 约 9.65599148388557
[/spoiler]如果您掷一个骰子 20 次,那么至少一次击中所有六面的概率是多少?
[剧透=解决方案]
答案可以近似表示为 1 - (prob(没有 1) + prob(没有 2) + ... + prob(没有 6)) = 1 - 6*(5/6)^20 = apx. 0.84349568。
然而,这会导致双倍减去两种不同面从未掷出的情况。从六种面中选择两种面,一共有(6,2)=15种方法。任意两种给定面从未掷出的概率是(4/6)^20。我们需要将这些值加到概率中,因为它们在上一步中被减去了两次。所以,现在我们得到的结果是 1 - 6*(5/6)^20 + 15*(4/6)^20 = 约 0.84800661。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
然而,如果任何一组从未掷出的三面在第一步中被三次减去,在第二步中被三次加去,我们需要将它们减去,因为六面中并非所有面都掷出了。从六面中选择三面共有 combin(6,3) = 20 种方法。任何特定的三面从未掷出的概率是 (3/6)^20。所以,现在我们得到的结果是 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20= 约 0.847987537。
然而,如果任何一组从未掷出的四面在第一步中被减去四倍,在第二步中被加去四倍,在第三步中被减去四倍,我们需要将它们加回去,因为每个这样的状态已经被减去了两次。从六面中选择四面,共有 combin(6,4) = 15 种方法。任何特定的四面从未掷出的概率是 (2/6)^20。所以,现在我们得到的结果是 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 = 约 0.84798754089。
然而,如果20次掷出的点数都相同,那么第一步就应该减去五倍,再加去五倍,第三步再减去五倍,第四步再加去五倍。我们需要把这些点数减掉。所以,现在我们得到的结果是:1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 - 6*(1/6)^20 = 约 0.84798754089。
所以答案是 1-6*(5/6)^20+COMBIN(6,4)*(4/6)^20-COMBIN(6,3)*(3/6)^20+COMBIN(6,2)*(2/6)^20-6*(1/6)^20 = 约 0.84798754089。[/剧透]
你有两个骰子。你可以随意给两个骰子的每一面编号,只要每一面都是大于或等于1的整数即可。你可以在同一个骰子上重复相同的数字,并且可以随意增加点数。除了制作标准骰子外,如何给它们编号,使任何给定点数的概率都与标准骰子相同?
骰子 1 = 1,2,2,3,3,4。
骰子 2 = 1,3,4,5,6,8。
恐怕我对这个问题的解决方案基本上是反复试验。
使用两个骰子,要获得从 2 到 12 的总数,平均需要掷多少次?
[剧透=解决方案]
这个问题可以用马尔可夫链来回答,但我更喜欢用微积分。关键在于,如果投掷间隔时间服从均值为1的指数分布,答案是一样的。也就是说,答案可以表示为从0到无穷大的积分:
1-(1-exp(-x/36))^2*(1-exp(-x/18))^2*(1-exp(-x/12))^2*(1-exp(-x/9))^2*(1-exp(-5*x/36))^2*(1-exp(-x/6))
您可以使用积分计算器轻松解决此类积分。
您也可以使用我的预期试验次数计算器来解决任何此类问题。
[/spoiler]投掷死亡游戏 (Drop Dead) 使用五个标准骰子进行。回合开始时,您需掷出所有五个骰子。如果所有骰子都不是 2 或 5,则计算所有骰子点数之和,并将结果添加到您的点数中,然后重新掷骰。如果掷出任何 2 或 5,则您的本轮得分为零。所有显示 2 或 5 的骰子均视为死局,并作废。然后,您使用剩余的骰子重新掷骰。游戏继续,您可以选择得分或移除骰子。当所有骰子都被移除后,您的回合结束,即您被判定为投掷死亡。所有得分将加在一起,得出您的最终得分。得分高者获胜。
您对这场比赛的预期得分是多少?
[剧透=解决方案]
让我们从剩下一个骰子的场景开始并向后移动。
设变量 a 为剩余一个骰子时的预期附加点数。
除 2 或 5 之外的平均掷点数为 (1+3+4+6)/4 = 7/2。
a = (2/3)×(a + 7/2)。
a/3 = 7/3。
a = 7。
接下来我们计算一下剩下两个骰子的预期点数b。
b = (2/3) 2 ×(b + 2 × (7/2)) + 2×(2/3)×(1/3)×a。
b = 11.2。
接下来我们计算一下剩下三个骰子的预期点数c。
c = (2/3) 3 ×(c + 3× (7/2)) + 3×(2/3) 2 ×(1/3)×b + 3×(2/3)×(1/3) 2 ×b。
c = 1302/95 = 13.705263。
接下来,我们来计算剩下四个骰子的预期点数d。
d = (2/3) 4 ×(d + 4× (7/2)) + 4×(2/3) 3 ×(1/3)×c + 6×(2/3) 2 ×(1/3) 2 ×b + 4×(2/3)×(1/3) 3 ×a。
d = 3752/247 = 15.190283。
最后,我们来计算一下剩下五个骰子的预期点数e。
e = (2/3) 5 ×(e + 5×(7/2)) + 5×(2/3) 4 ×(1/3)×d + 10×(2/3) 3 ×(1/3) 2 ×c + 10×(2/3) 2 ×(1/3) 3 ×b + 5×(2/3)×(1/3) 4 ×a。
e = 16.064662。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
反复掷两个骰子,一个红色骰子,一个蓝色骰子。记录每个骰子的点数之和。当两个骰子点数相等时,预期角色数是多少?
[剧透=更多评论]
很难解释为什么答案是无穷大。更令人困惑和矛盾的是,总数相等的概率是1。
下表显示了 1 至 16 次投掷后总数首次相同的概率。
概率首次等于总数
| 面包卷 | 可能性 |
|---|---|
| 1 | 0.166667 |
| 2 | 0.112654 |
| 3 | 0.092850 |
| 4 | 0.080944 |
| 5 | 0.072693 |
| 6 | 0.066539 |
| 7 | 0.061722 |
| 8 | 0.057819 |
| 9 | 0.054573 |
| 10 | 0.051819 |
| 11 | 0.049443 |
| 12 | 0.047367 |
| 十三 | 0.045532 |
| 14 | 0.043895 |
| 15 | 0.042423 |
| 16 | 0.041089 |
Excel 显示与该曲线非常接近的拟合值为 y = 0.1784*x-1.011,其中 x = 滚动次数,y = 概率。
这个无穷级数的和是无穷大。
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
掷五个红色骰子和五个蓝色骰子。无论掷骰子的顺序如何,掷出相同点数的概率是多少?例如,掷出的点数都是 1-2-3-3-6。
下表显示了任何类型的卷:
- 掷出此牌型的不同组合数。例如,对于葫芦,三条有六种组合,对子有五种组合,总共有30种不同的葫芦组合。
- 顺序数。例如,对于葫芦,有 combin(5,3)=10 种方法可以从五个骰子中选择三个组成三条。另外两个骰子必须组成对子。
- 给定牌型的掷出方式数量。这是前两列的乘积。例如,葫芦有 30 * 10 = 300 种掷出方式。
- 手牌的概率。例如,葫芦的概率为 300/6 5 = 0.038580。
- 两次掷出相同点数且属于给定牌型的概率。这是第四列概率的平方除以第二列。例如,两次掷出相同点数的概率为 0.038580 2 。然而,两次掷出相同点数的概率为 1/30。因此,两次掷出相同点数的概率为 0.038580 2 /30 = 0.00004961。
右下角单元格显示两次掷骰结果相同的总概率为 0.00635324。
匹配卷
| 类型 卷 | 不同的 类型 | 订单 | 全部的 组合 | 可能性 一卷 | 可能性 两卷 | |
|---|---|---|---|---|---|---|
| 五张相同的牌 | 6 | 1 | 6 | 0.00077160 | 0.00000010 | |
| 四条 | 三十 | 5 | 150 | 0.01929012 | 0.00001240 | |
| 客满 | 三十 | 10 | 300 | 0.03858025 | 0.00004961 | |
| 三条 | 60 | 20 | 1,200 | 0.15432099 | 0.00039692 | |
| 两对 | 60 | 三十 | 1,800 | 0.23148148 | 0.00089306 | |
| 一对 | 60 | 60 | 3,600 | 0.46296296 | 0.00357225 | |
| 五个单身人士 | 6 | 120 | 720 | 0.09259259 | 0.00142890 | |
| 全部的 | 7,776 | 1.00000000 | 0.00635324 |
掷一个六面骰子,直到发生以下任一事件:
A) 任何一方都出现了六次。
B) 每一方都至少出现过一次。
事件 A 首先发生的概率是多少?
为了像我一样使用微积分来回答这个问题,我推荐使用积分计算器,例如integral-calculator.com/上的那个。
这是我的解决方案(PDF)。
我在Wizard of Vegas论坛上提出过这个问题(用略有不同的措辞)并讨论过这个问题。
你想玩一个需要普通六面骰子的游戏。很遗憾,你把骰子弄丢了。不过,你有四张索引卡,你可以随意标记。玩家必须从这四张卡中随机选择两张,不能重复,然后计算两张卡的点数之和。
如何给卡片编号,使得两张不同卡片的总和代表掷骰子的次数?
给它们编号为 0、1、2 和 4。
从四张牌中抽出两张的方法有以下六种。
- 0+1=1
- 0+2=2
- 1+2=3
- 0+4=4
- 1+4=5
- 2+4=6
我在Wizard of Vegas论坛上提出并讨论了这个问题。
一枚六面骰子反复掷出,直到总点数达到或超过13。最终点数的平均值、中位数和众数是多少?
中位数 = 14
模式 = 13
[剧透=解决方案]
我不得不用马尔可夫链来解决这个问题。下表根据左列的累计和显示了每个最终总数的概率。首先从 13 到 18 的明显情况开始。然后,对于 0 到 12 的累计和,取下面六个单元格的平均值。
可以在第一行中找到初始状态的概率,其总和为 0。
马尔可夫链
| 掷骰子总数 | 十三 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|
| 0 | 0.279263 | 0.236996 | 0.192313 | 0.145585 | 0.097371 | 0.048472 |
| 1 | 0.290830 | 0.230791 | 0.188524 | 0.143842 | 0.097114 | 0.048899 |
| 2 | 0.293393 | 0.241931 | 0.181893 | 0.139625 | 0.094943 | 0.048215 |
| 3 | 0.289288 | 0.245178 | 0.193717 | 0.133678 | 0.091410 | 0.046728 |
| 4 | 0.280369 | 0.242560 | 0.198450 | 0.146988 | 0.086950 | 0.044682 |
| 5 | 0.268094 | 0.235687 | 0.197878 | 0.153768 | 0.102306 | 0.042267 |
| 6 | 0.253604 | 0.225827 | 0.193419 | 0.155611 | 0.111500 | 0.060039 |
| 7 | 0.360232 | 0.193566 | 0.165788 | 0.133380 | 0.095572 | 0.051462 |
| 8 | 0.308771 | 0.308771 | 0.142104 | 0.114326 | 0.081919 | 0.044110 |
| 9 | 0.264660 | 0.264660 | 0.264660 | 0.097994 | 0.070216 | 0.037809 |
| 10 | 0.226852 | 0.226852 | 0.226852 | 0.226852 | 0.060185 | 0.032407 |
| 11 | 0.194444 | 0.194444 | 0.194444 | 0.194444 | 0.194444 | 0.027778 |
| 12 | 0.166667 | 0.166667 | 0.166667 | 0.166667 | 0.166667 | 0.166667 |
| 十三 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 14 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 15 | 0.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 |
| 16 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 |
| 17 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 0.000000 |
| 18 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
这个问题是在我的论坛“ 拉斯维加斯巫师”中提出并讨论的。
如您所知,如果在掷出 7 之前掷出从 2 到 12 的所有数字(除 7 之外),则掷骰子游戏中的“全部下注”获胜。如果获胜,平均需要掷多少次才能赢得这个赌注?
我看到有人声称在掷骰子游戏桌上连续目击了18个(总共11个)的“young”(年年有余,指年年有余,指年年有余)。平均需要掷多少次才能观察到这种情况?
这是我的解决方案(PDF)。
一对公平的六面骰子被反复掷出,直到发生以下两个事件之一:
A) 总共掷出 12 点。
B) 连续两次掷出总数为 7。
哪一个更有可能先发生?
> [剧透=解决方案]
让:
- p = 从初始状态开始首先掷出 12 的概率,或者当前一次掷出的点数不是 7 时。
- q = 上次掷出的点数为 7 时,首先掷出 12 的概率。
这就是所谓的马尔可夫链问题。
在我们讨论这一点之前,回想一下掷出总数 7 的概率是 1/6,掷出总数 12 的概率是 1/36。
我们可以根据 p 和 q 相互定义,如下所示:
- (1)p =(1/36)+(6/36)q +(29/36)p
- (2)q = (1/36) + (29/36)p
我们将公式 (1) 乘以 36:
36便士=1+6q+29便士
(3)7p = 1 + 6q
我们将 (2) 式中的 q 值代入 (3) 式中:
7p = 1 + 6*((1/36) + (29/36)p)
7便士=1+(1/6)+(29/6)便士
42便士=6+1+29便士
13便士=7
q = 7/13
因此,首先掷出 12 的概率是 7/13 =~ 53.85%。
因此,首先掷出两个连续 7 的概率为 46.15%。
因此,更有可能的是首先掷出总数 12。



