⼆⼗⼀点 - 基本策略(特定牌型)
Wiz,你真是个好人!你的赌博网站绝对是网上最好的。作为一名精算师(ACAS),我很高兴看到有人能充分发挥自己的数学技能。
我的问题是——既然允许后期投降,你还想在10点亮牌的情况下分8点吗?我猜是的,但BJ中最难的玩法之一就是在10点亮牌的情况下分8点。
顺便提一下,我刚在拉斯维加斯待了三天,如果你还没去过,一定要试试拉斯维加斯俱乐部和世界上最自由的二十一点规则。3张或4张牌可以加倍,6张牌<=21点自动赢,也可以晚点投降。六副牌,我估计庄家优势是0.14%。感谢你们的辛勤付出!
谢谢你的赞美,吉姆。是的,即使有人建议你晚点投降,你仍然应该分牌。即使分牌后不能加倍,你也应该拒绝投降。基于两副牌的游戏,分牌后不能加倍,那么分牌8对10的预期值为-0.480673,比投降的-0.5要好。
尽管他们声称拥有“世界上最自由的二十一点规则”,但在马蹄铁赌场(Horseshoe)或金门赌场(Golden Gate)街对面,却有更好的单副牌游戏。拉斯维加斯俱乐部(Las Vegas Club)的六副牌才是真正对玩家不利的。别因为被他们的招牌所蒙蔽而感到难过,我年轻时也曾上当受骗,那时我还不知道规则变化的后果。
更新:这个问题之后,拉斯维加斯俱乐部修改了规则,在他们所谓的“世界上最自由的二十一点规则”中,对二十一点的赔率是6比5。6比5甚至不能算作真正的二十一点游戏。在任何普通的3比2游戏中,你的赔率都要高得多,这种游戏在其他地方很容易找到。
单副牌二十一点的牌是面朝下发的吗?单副牌的一般规则是什么?我知道您提到只有9-11或10-11点才可以加倍,但您知道单副牌的分牌后加倍、庄家要牌软17点等等的一般规则是什么吗?我是一个基础策略型玩家,想了解单副牌的规则(我只玩过6副或8副牌),这样我就可以从blackjackinfo.com网站获取完美的电子表格。非常感谢您的帮助!
单副牌二十一点的规则通常很严格。牌面朝下发牌。加倍通常限制在9比11或10比11。庄家拿到软17点后加倍,分牌后可能不允许加倍。如果二十一点的赔率低于3比2(单副牌游戏通常如此),请务必不要玩。
您可以在我的“拉斯维加斯巫师”网站上随时查看拉斯维加斯相对较新的二十一点规则。
你的二十一点策略是,对A、10、9,你弃牌16。你说要对着这些牌分牌,比如一对8。我听说一对8就是16,应该弃牌。你怎么看?
如果庄家查看底牌,发现没有黑杰克,那为什么要用软18对抗A呢?还有,为什么不在11点时加倍呢?
在二十一点游戏中,很少有简单的答案。你必须考虑所有可能发生的情况,并根据概率权衡每个结果。最佳玩法是预期回报最大的玩法。根据我的二十一点附录 9b ,在双层牌局中,用软 18 对抗 A 的预期回报是 -0.1004,停牌的预期回报是 -0.1005。因此,要牌只是稍微好一点。用 11 对抗 A 也是一种非常边缘的玩法。实际上,在单层和双层牌局中,它都取决于牌型,换句话说,取决于哪两张牌的总数为 11 来决定如何出牌。但是,如果你不想记住与牌型相关的基本策略例外,那么你应该在单层和双层牌局中用 11 对抗 A 时加倍下注,并用四副或更多牌要牌。
嗨!我很喜欢你的网站!如果我拿到黑杰克,而庄家亮出一张A,我可以选择赢等额的钱还是继续玩。我应该赢等额的钱还是继续玩?
这是看待投保决策的另一种方式。投保等额赌注的预期回报显然是 1.0 个单位的赌注。为简单起见,我们假设一副牌的数量是无限的。庄家拿到黑杰克的概率是 4/13,否则是 9/13。如果庄家拿到黑杰克,你就推牌。如果没有,那么你就赢 1.5 个单位。不投保的预期值为 (4/13)*0 + (9/13)*(1.5) = 13.5/13 = 1.0384615,大于 1.0。因此,拒绝投保或等额赌注并继续玩牌是更好的选择。在实际游戏中,如果牌组数量有限,赔率会更高,因为(你手中的)牌组中已经有一张 10,这降低了庄家拿到黑杰克的概率。
“你不可两面下注。”——《赌博十诫》(第七条)
迈克,上次我去拉斯维加斯的时候,我认识的一位荷官说,他“正在考虑”在庄家拿到16点牌时停牌,而庄家拿到7点牌时,因为8张牌中只有5张能让庄家自动获胜。这个策略该如何实施呢?
这会是一个糟糕的玩法。例如,我的二十一点附录 9B展示了用 10 和 6 张牌对抗庄家 7 点牌的两种情况的回报。拿牌的预期损失为赌注的 39.6%。然而,停牌的预期损失为 47.89%。我无法轻易解释为什么拿牌更好。你必须考虑所有可能发生的情况,用概率加权,然后取总和。总的来说,拿牌是两种糟糕玩法中更好的选择。
关于附录6中提到的投降例外情况,我该如何将其更好地运用到统一游戏的单副牌游戏中,在面对A牌时提前投降?感谢你的帮助和很棒的网站。
谢谢你的赞美。在统一游戏 (Unified Gaming) 的二十一点游戏中,只有当庄家亮出 10 点时,你才应该使用附录六。当庄家亮出 A 点时,统一游戏 (Unified Gaming) 的基本策略没有例外。
我刚从哥斯达黎加回来。他们给二十一点赔率是1比1。这对赌场来说值多少钱?如果我拿到21点,而庄家拿到3比6,我是不是应该加倍下注?毕竟我的赔率只有1比1。
请参阅我的拉米牌页面,拉米牌是在哥斯达黎加流行的二十一点变体。
您好,我刚刚看了您的 Microgaming 二十一点基本策略卡。我注意到,在 7,7 点牌时,您建议玩家不要在 10 点牌时拿牌。这是为什么?这是否会影响在 14 点牌时拿牌的建议?
在我所有的单副牌二十一点策略中,这都是正确的玩法。原因是拿到第三个7的概率只有2/49,大约是4.08%。相比之下,双副牌的概率是6/101,也就是5.94%。由于赢庄家20的希望不大,最好是拿牌,或者如果可以的话投降。没错,这确实推翻了我之前建议的用14来对付10的建议。
我做荷官已经十年了,一直在努力摆脱这个职业。我数不清有多少次听人说:“永远假设底牌是10。” 你我都知道,这话不可能总是对的。我理解他们为什么这么说,但是,它真的就是10的概率有多大呢?如果荷官手里有一张A,你用读卡器检查牌型,发现不是黑杰克,你肯定知道它不是10。那么,你又该假设它是什么呢?
我也不喜欢这个说法。它充其量只是一种记忆手段,帮助人们记住,如果庄家的牌是7到10,就应该打硬牌。没有一条简单的经验法则适用于所有情况。
我在二十一点网站上研究你的附录1时,发现了一些奇怪的事情。六副牌游戏的基本策略(分牌后加倍,庄家在软17点不动等等——所有常见的脱衣舞规则)规定,如果庄家拿到5,A,2可以加倍。然而,附录中却指出,如果玩家拿到A,4,庄家拿到4的预期回报会更高(拿牌的预期回报为0.1334,加倍的预期回报为0.126)。如果玩家拿到A,4,庄家拿到4,预期回报也更高(拿牌的预期回报为0.0593,加倍的预期回报为0.0584)。其他所有分牌和加倍都有效。这两个例子是怎么回事?提前致谢。
附录1基于无限套牌。你提到的两种牌型都是边界牌型,套牌数量会影响哪种打法更好。例如,A-4 对抗 4 时,用 26 副牌加倍,用 27 副牌要牌。A-2 对抗 5 时,套牌数量也介于 8 副牌到无限副牌之间。
作为一名BJ玩家,我经常用10对着爆牌分牌。这个举动的期望值是正数,但不如原地不动那么有利可图。你能告诉我这位朋友,在中立牌组中,分牌10比原地不动要差多少吗?另外,很多BJ玩家会因为有人用10对着6分牌分牌而感到不满,但他们自己也经常用2或7对着10分牌分牌。你能解释一下吗?
我煞费苦心地编写了二十一点附录 9A-9H 来解答这类问题。例如,在六副牌的游戏中,如果庄家在软 17 点停牌,您可以使用二十一点附录 9G。从中可以看出,如果庄家拿到两张 10 点,而庄家拿到 6 点,停牌的预期收益为 0.702826。在这种情况下,分牌的预期收益为 0.622165。因此,玩家停牌比分牌可以多赢 8.07%。不要太在意其他玩家在二十一点牌桌上的言行。
Wiz,这是一个关于庄家10点,8点分牌的问题。分牌在单手牌中是正确的玩法。但是,我认为对于典型的二十一点玩家来说,考虑到你要加倍下注,最好是停牌。为什么要在赔率这么低、远低于平均水平的情况下加倍下注呢?毕竟,目标是最大化你的总回报(即所有投注的加权平均值)。请问您有什么看法?
PS:您的网站很棒,横幅广告和侧边栏等广告是可以理解的,但像弹出窗口和问题提示这样的侵入性广告试图强迫您访问另一个网站,在我看来有点过分了。
虽然这局牌势均力敌,但停牌是第三糟糕的选择。使用我的二十一点附录9G,我们可以得出以下预期收益:
- 支架-.536853
- 命中 -.535361
- 拆分 -.474733
- 双倍 -1.07022
分牌是最佳选择,因为它能将牌局的总损失降至最低。加倍和分牌的预期收益基于该牌局相对于初始下注的总收益。例如,如果你的初始下注是100美元,然后你分牌,所有因素加起来,总预期损失为47.47美元,低于不加注的预期损失53.69美元。
双重曝光的牌表显示,如果庄家有13-16点,就分牌10。这是否意味着你还要继续分牌10?我曾经这样做过,结果四手牌都低于18点,全部输了。幸好当时我只是在某个网络游戏网站上玩玩而已。
是的,只要你一直拿到10,就应该继续分牌。玩一手牌输了并不能证明什么。必须双向玩数百万手牌,并将结果汇总起来,才能真正找到最佳玩法。
在四副牌的二十一点游戏中,如果你用A对5或6分牌,然后你又拿到一张A,你应该加倍还是要牌?(目前不再讨论分牌)我在不同的网站上得到了不同的答案。到目前为止,我看到一个网站在5和6时加倍,一个网站只在6时加倍,其他网站列出了所有情况下的分牌,我猜他们没有考虑这种情况。另一个问题是,在四副牌的二十一点游戏中,用10、2对4,一个网站列出了要牌。我想请您确认一下。
请记住,大多数赌场不允许您这样做。但是,如果可以,您应该只在 6 上加倍。无论庄家是否拿到软 17 点,这都是正确的。如果庄家在软 17 点上停牌,那么面对 5 点,拿牌的预期回报是 0.162849,加倍是 0.148228,所以拿牌是更好的玩法。面对 6 点,拿牌的预期回报是 0.189020,加倍是 0.196249。所以加倍是更好的玩法。您可以在我的二十一点附录 9e中亲自查看这些数字。关于您的另一个问题,是的,在 4 副牌的游戏中,玩家应该拿 10.2 对抗 4,但前提是庄家在软 17 点上停牌。我自己没有列出 4 副牌基本策略例外,因为例外很少,而且差别很小。遵循这个例外情况,你每113396手就能赢更多单位,或者说,赌场优势降低0.000882%。在我看来,不值得费心记住这个例外情况。
在您的二十一点附录 6中,关于后期投降,您建议在庄家拿到 10 时投降 10+5 和 9+6。在统一游戏的基本策略中,您建议在庄家拿到 10 时拿 15。我不明白为什么在这种情况下要拿牌而不是投降,因为 9+6 和 10+5 比 8+7 更有可能拿到 15。
这是一个有趣的情况。虽然在单副牌中,15点对10点时你应该有5/6的概率投降,但总是要牌总比总是投降要好。以下是每次要牌凑成15点的预期收益。
- 10+5
- -.501091
- 9+6
- -.509827
- 8+7
- -.474794
有四种方法可以凑成10+5,而其他两种方法各只有1种。因此,在一副牌中,如果点数为15,而点数为10,则总预期回报为 (4/6)*-.501091 + (1/6)*-.509827 + (1/6)*-.474794 = -.498164。换句话说,点数为10、5和9、6的概率略高,而点数为8、7的概率则高得多。8、7的预期回报更高的原因是,牌堆里仍然有5和6,因此点数为20或21的概率更大。
我的问题是关于BJ的赌桌最高下注额。假设官方公布的下注额度是200美元。我下注200美元,拿到8-3的牌。我可以加倍吗?或者,假设我下注200美元,拿到一对A。我可以把牌分成两手吗?
是的,在这种情况下,您可以加倍或分牌。最高限额适用于初始下注。如果限额为 200 美元,您也可以玩多手 200 美元的牌。
我刚刚读到一篇文章,说在多副牌(4副或更多副牌)的二十一点游戏中,如果庄家的牌是10,并且包含4或5,那么正确的基本策略是停牌。我查看了你们的网站,发现只找到了单副牌和双副牌游戏中多张牌的附录。这篇文章对吗?
是的!好问题,连我都不知道这一点。牌堆越少,牌的数量越多,这种情况就越明显。为了测试最有可能击中的情况——8 副牌堆,只有 3 张牌——我用我的组合程序运行了所有可能的情况。下表显示了结果。
8 副牌游戏中 3 张牌 16 对 10 的预期值
| 手 | 电动汽车热销 | 电动车支架 | 最好的 玩 | 可能性 | 返回 打 | 返回 站立 |
| 2010年1月5日 | -0.540978 | -0.539872 | 站立 | 0.132024 | -0.071422 | -0.071276 |
| 1/6/9 | -0.536558 | -0.540151 | 打 | 0.059837 | -0.032106 | -0.032321 |
| 1/7/8 | -0.537115 | -0.537003 | 站立 | 0.059837 | -0.032139 | -0.032133 |
| 2010年2月4日 | -0.540947 | -0.541 | 打 | 0.237478 | -0.128463 | -0.128475 |
| 2/5/9 | -0.542105 | -0.540534 | 站立 | 0.039891 | -0.021625 | -0.021563 |
| 2/6/8 | -0.537701 | -0.540773 | 打 | 0.059837 | -0.032174 | -0.032358 |
| 2/7/7 | -0.538271 | -0.537584 | 站立 | 0.028983 | -0.015601 | -0.015581 |
| 2010年3月3日 | -0.540385 | -0.540995 | 打 | 0.115028 | -0.06216 | -0.06223 |
| 3/4/9 | -0.541769 | -0.540536 | 站立 | 0.059837 | -0.032418 | -0.032344 |
| 3/5/8 | -0.54295 | -0.540022 | 站立 | 0.039891 | -0.021659 | -0.021542 |
| 3/6/7 | -0.538575 | -0.540228 | 打 | 0.059837 | -0.032227 | -0.032326 |
| 4/4/8 | -0.543188 | -0.54003 | 站立 | 0.028983 | -0.015743 | -0.015652 |
| 4/5/7 | -0.544396 | -0.539483 | 站立 | 0.039891 | -0.021717 | -0.021521 |
| 4/6/6 | -0.539446 | -0.542878 | 打 | 0.028983 | -0.015635 | -0.015735 |
| 5/5/6 | -0.545033 | -0.542137 | 站立 | 0.009661 | -0.005266 | -0.005238 |
| 全部的 | 1 | -0.540355 | -0.540293 |
底行右侧的两个数字表明,要牌的总体预期值为 -0.540355,停牌的总体预期值为 -0.540293。因此,停牌是略微更好的打法。遵循这条规则,每 1117910 手牌就能额外获得一个单位。这条建议需要玩家每周玩 40 小时的二十一点,大约需要 5 年时间才能让他节省一个单位。
我喜欢用你的二十一点附录3来调整我的在线单副牌二十一点玩法。我看到你在12月更新了这个页面,似乎在双牌部分有一些新的玩法。我不明白为什么建议用10和2对抗4,尤其是在庄家爆牌可能性很大的6的情况下。而且,真的可以对抗4,而不能对抗5,用10和2就对了吗?!我很感激你能提供任何见解。关键在于庄家可以同时持有6和A吗?嗯,这很有道理。这些是新策略吗?如果是,是什么促使它们产生的?
是的,我对两张牌的牌型列表做了一些修改。我删除了“9+3 对 3”,并添加了“10+2 对 6”。在单副牌游戏中,如果庄家拿到软 17 点停牌,而玩家拿到 10+2 点,庄家拿到 6 点,那么拿牌的预期值为 -0.159436,而停牌的预期值为 -0.160379。因此,拿牌的平均损失较小。我不想对基本策略给出简明扼要的答案,因为牌的出牌方式多种多样。庄家拿到 6 点爆牌的概率更大。然而,正如你所说,庄家拿到 6 点而不是 5 点时,拿到 17 点的可能性也更大。17 点不是好牌,会促使玩家拿牌并试图击败它。
如果你有15点,而庄家亮出8点……基本策略是要牌。在这种情况下,无论你要牌还是停牌,你输的概率都超过70%……既然无论你要牌还是停牌,你的输概率都超过70%,为什么投降不是更好的选择呢?
为了简单起见,我们继续使用你的例子,假设你击中了,获胜的概率是70%,失败的概率是30%。击中的预期值为0.3*1 + 0.7*-1 = -0.4。这大于投降的预期值-0.5。
我只是想确认一下,在Microgaming的单副牌游戏中,A,A vs A的正确玩法是按照你的基本策略卡上显示的分牌。我非常确定正确的玩法应该是拿牌,至少在四副牌的情况下是这样。而且看起来,如果所有10都还剩下,你很可能经常会输掉两倍的赌注。我不是不相信你,只是想确认一下。你有没有想过,这手牌拿牌和分牌的期望值是多少?
我曾多次被问及这个问题,并始终坚持认为,尽管输掉了全部赌注,但抽牌分牌A的选择克服了欧洲的“不偷看”规则,因此分牌是更好的玩法。基于一副牌,每手牌的预期价值(考虑到庄家拿到黑杰克的可能性)为:要牌-0.532849,分牌-0.223277。因此,分牌比四副牌更好,大约31%的单位。对于四副牌的游戏来说,分牌也是更好的选择,Microgaming 的玩家不应该玩四副牌游戏,因为有同样规则的单副牌游戏可供选择。
在对二十一点进行无限套牌分析之后,我偶然发现了您的网站,分析规则和您的一样(庄家所有17点停牌,除了Ace只能分牌一次外,其他四手牌都可以重新分牌,分牌后加倍,分牌Ace时只抽一张牌)。在比较预期值时,我得出的结果和您一样,除了对子分牌略有不同。所以我想知道您是如何计算分牌预期值的?
我花了好几年才自己弄好分牌对子。Gambling Tools的 Cindy 给了我很大的帮助。Peter Griffin 在《二十一点理论》第 11 章中也谈到了这个话题。假设我想计算庄家 2 点时分牌 8 的期望值。最多可以重新分牌 4 手。以下是我的做法。
- 从鞋子里取出一张 2 和两张 8。
- 确定玩家不会在任何一手牌中拿到第三个八的概率。
- 遍历除 8 之外的所有点数,从牌堆中减去该点数,用该点数和 8 打出一手牌,确定期望值,然后乘以 2。假设另一个 8 的概率为零,则确定每个点数对应的概率。将每个点数对应的概率与期望值进行点积。
- 将此点积乘以步骤 2 中的概率。
- 确定玩家重新分牌为 3 手的概率。
- 从牌堆中再取出 8。
- 重复步骤 3,但乘以 3 而不是 2。
- 将步骤 7 中的点积乘以步骤 5 中的概率。
- 确定玩家重新分牌为 4 手的概率。
- 从鞋子里取出另外两个 8。
- 重复步骤 3,但乘以 4 而不是 2,这次考虑获得 8 作为第三张牌,对应于玩家被迫停止重新分牌的情况。
- 将步骤 11 中的点积乘以步骤 9 中的概率。
- 添加步骤 4、8 和 12 中的值。
最难的部分是第三步。我有一个非常难看的子程序,里面全是我用概率树计算的长公式。当庄家拿到10或A时,它就变得特别难看了。
我有个关于你的八副牌二十一点策略的疑问。首先,这个问题背后的基本假设是,拿到软17点对庄家有利。为什么这个策略要求玩家在庄家可能拿到软17点(例如,庄家亮出A或6)的情况下更频繁地加倍,而在庄家拿到软17点停牌的情况下却不加倍?如果拿到软17点能让庄家更有优势,为什么玩家会在这种时候投入更多资金呢?这两个图表可能互换了吗?
你说得对,一般来说,拿到软17点对庄家有利。但这只是一个普遍规律,并非适用于所有情况。当你手牌强到18到21点时,你希望庄家在软17点停牌。然而,如果你手牌弱到17点以下,你希望庄家拿到软17点。举个策略差异的例子:当庄家拿到软17点时,你应该用软19点对6加倍;如果庄家拿到软17点停牌,你应该停牌。这是因为加倍很可能抽到坏牌,导致点数达到16点或更低。当庄家拿到软17点时,他爆牌的次数更多,所以在这个例子中,加倍会更安全一些。
您已经向我展示了如何在玩掷骰子时盈利。谢谢!现在您的网站正在教我玩二十一点。我有个问题:比如说,当你拿到两张5,想要加倍下注时,你会在原先的赌注旁边再加注。那么,荷官怎么知道你不是想分牌呢?谢谢!您的网站太棒了!
谢谢你的赞美。要回答你的问题,荷官会直接问你想做什么。通常情况下,二十一点的所有决定都必须清晰可见,但这是我能想到的唯一例外。不过,如果你想避免轮到你时被问到,只需举起食指表示你想要一张牌。大多数荷官都知道这意味着什么。巧合的是,我昨天才知道,在保加利亚,如果你想加倍,就把额外的赌注放在原赌注后面;如果你想分牌,就把额外的赌注放在原赌注旁边。
另一位读者写信说,在北达科他州,州法律规定要遵循保加利亚规则来处理加倍和分割。
你的二十一点基本策略表上写着,如果庄家的牌是3-6,A、7点牌“如果允许就加倍,否则停牌”。我的问题是,为什么要停牌?如果你愿意加倍却不能,那么至少在可以拿牌的情况下应该要牌吗?反正你也愿意再拿一张牌。谢谢你抽出时间!
如果玩家可以选择加倍下注并停牌,那会比传统的加倍更好。因此,在这种情况下,拿牌实际上对玩家的牌不利,但为了赢得双倍的筹码,这样做是值得的。
二十一点的基本策略图规定,如果庄家有一张A,那么在16点时就应该加牌。我想知道,这个策略图是否考虑到了这样一个事实:一旦知道保险不赔付,庄家就不会再有10点的牌了?这显然降低了庄家拿到好牌的几率,但玩家拿到16点就应该停牌吗?
是的,基本策略假设庄家没有10。即使在庄家不过牌的欧洲,要牌/停牌策略也是一样的,因为如果庄家有黑杰克,玩家就毫无希望了。假设庄家有一张A,而没有黑杰克,庄家在软17点停牌时,拿到17点或以上的概率是83.3%。所以停牌甚至不是一个很危险的玩法,要牌的概率绝对更大。
如果庄家没有在牌面显示 10 的情况下检查是否有黑杰克,而是在牌局结束时只拿走原始赌注,这是否需要改变策略?
不。只要你只输掉原始赌注,就应该假设庄家没有黑杰克。如果庄家真的有黑杰克,你也无能为力。
你提出了一个数学上的论证,证明玩家应该拒绝保险。然而,你的心理学论证却站不住脚。大多数人会觉得,为了争取1.5个“林中鸟”而放弃手中的一只鸟,就像个傻瓜。
哦,赌博就是要冒险。成功的赌徒不会试图最大化每手牌的净赢概率,而是会冒险最大化他的总回报。无论是在赌博还是在生活中,有时为了长期利益,都必须承担短期风险。所以,少考虑现在,多考虑未来。
为什么您的 Blackjack Switch 基本策略表说总是在 12 点时要拿牌?
在二十一点转换游戏中,玩家应该更积极地要牌,因为庄家点数为22点会导致平局。在常规二十一点游戏中,停牌的价值很大程度上体现在庄家爆牌时。而在二十一点转换游戏中,许多庄家的赢牌都会转化为平局,相比之下,要牌是更好的选择。
我老婆懂二十一点的基本策略,但她坚持要靠直觉打牌。请问哪些牌型最接近50-50,这样我老婆就能把直觉打法限制在这些牌型上?
我确信这个问题已经有人回答过了,但这是个好问题,所以我再回答一次。以下是一些边缘玩法,以算牌指数为零为依据。此列表适用于多副牌的情况,其中庄家在软17点停牌,允许分牌后加倍。最佳玩法列在最前面,其他玩法列在后面。
- 9 对 2(击中/加倍)
- 12 对 4(停牌/要牌)
- 12 对 6(停牌/要牌)
- 16 对 10(要牌/停牌)
- 软 13 对 5(加倍/击中)
- 软 15 对 4(加倍/击中)
- 3、3 对 2(分牌/要牌)
我翻遍了你们的二十一点板块,就是没找到“怎么”投降。我知道投降是怎么回事,但我是不是只拿一半筹码就完事了?
不,下注后直到牌局结束都不能动你的筹码。投降的信号是用食指在二十一点牌桌上,从左到右,在你的筹码后面假装画一条线。我之前甚至不知道这一点,直到最近一位欧洲朋友在牌桌上做了这个动作。直接说“投降”也一样有效。
为什么说在Blackjack Switch游戏中,当数字为 10 或 11 时,面对数字 9 时不要加倍下注?
原因是,如果庄家拿到22点,而你的牌是21点或更少,那么就推牌。这非常有利于庄家,应该会抑制你通过加倍或分牌来增加筹码。
前几天我听说,如果你玩的是6:5的牌局(或者里约的等额赔付牌局),拿到天生牌时应该加倍下注,以抵消较低的赔付。是这样吗?这种玩法的预期损失是多少?
这会是一个糟糕的玩法。例如,如果你在黑杰克上对着5点(六副牌庄家在软17点停牌)加倍,根据我的黑杰克附录9I ,你的预期收益将是0.622362。所以,即使在等额投注游戏中,这仍然是一个错误,损失了大约38%的赌注。
Wong在《专业二十一点》第23页写道:“如果你以10-2或2-10(其中10表示任何10点牌)的点数拿到12点,并且使用两副或更少的牌(或者如果庄家在软17点停牌,则使用七副或更少的牌),你应该要牌。” 对吗?我理解在一副或两副牌的游戏中,依赖牌型的策略有一定的价值,但他说的是,当使用七副牌(S17)时,你应该要牌10-2/2-10!这听起来不对。
Wong 指的是玩家 12 对抗庄家 4,并引用了 Peter Griffin 所著的《二十一点理论》第 176 页。是的,他是对的。在七副牌的游戏中,要牌的预期值为 -0.210820,停牌的预期值为 -0.211106,因此要牌更高。但是,八副牌的游戏中,要牌为 -0.2111161,停牌为 -0.211100,因此停牌更高。这是一种非常不确定的玩法,七副牌和八副牌之间确实存在牌数差异。这里有一个更好的例子。用 A-4 对抗 4,你应该一直加倍直到有 26 副牌,但用 27 副或更多牌来要牌。
当现金返还适用于总投注金额时(从而给玩家额外的加倍或分牌动力),在互联网上加倍或分牌有什么基本策略例外吗?请假设现金返还率为0.1%。
我找不到任何一手牌,额外的0.1%的筹码量会导致策略改变。我能找到的最接近的例子是,基于六副牌,庄家在软17点停牌,A,4对4。在这手牌中,加倍会让玩家的预期价值损失略低于要牌的0.3%。所以,如果你能拿到0.3%或更多的筹码量,那就加倍这手牌。我研究过的其他边缘牌型,玩家加倍或分牌至少要损失1%,而且我从未见过二十一点中返现如此之高。
在二十一点中,16 对 10 的策略是 R,S,因为一旦您淘汰了 2 张牌,则对于任何数量的牌组,策略都是停牌(不拿牌)。
确实,一般来说,如果玩家有三张或更多张牌,16 点对 10 点时应该停牌。所以,如果我的图表是基于赌场提供投降选项的,那么你是正确的。然而,这个假设并非如此。如果我将规则改为 Rs(如果允许投降则投降,否则停牌),那就意味着如果不允许投降,玩家应该在两张牌 16 点对 10 点时停牌。
在您的二十一点附录9中,您指出玩家面对10点时,有正期望值击中10点?例如,假设玩家有六副牌,而玩家的10点由6和4组成,您指出玩家优势为0.026796 。难道玩家和庄家都要到17点才能拿牌吗?这应该会给庄家带来优势,因为如果双方都爆牌,庄家就会赢。
原因是玩家的下一张牌可能是A,但庄家的下一张牌不是。我在附录的解释中已经提到,我已经假设庄家没有黑杰克。这就是为什么在庄家偷看并确认自己没有黑杰克后,玩家在这种情况下略占优势。
在大多数二十一点计数系统中,16对10的索引号是零。所以,如果牌堆完全是中性的,你应该停牌,因为如果点数等于或超过索引号,你就停牌。然而,基本策略表告诉我们要牌。这似乎自相矛盾。
说实话,这是一个老问题了,但我从 Chris F. 那里得到了更好的答案。他正确地指出,原因在于,在创建基本策略图表时,他们假设玩家的前两张牌和庄家的明牌已经从牌堆中移除。一个很好的例子是,在单副牌中,正确的玩法是,当牌堆中有 7,7 时,对 10 停牌,因为牌堆中一半的 7 已经消失了,而这正是你用 3 张牌击败庄家 20 所需要的。
在16对10的情况下,玩家的手牌要么是10和6,要么是9和7。无论哪种情况,两张会因为要牌而爆牌的牌都被移除了。因此,牌堆里有一些不会爆牌的小牌,这给了玩家要牌的动力。虽然这是事实,但我还是持怀疑态度,因为在无限牌堆游戏中,要牌的概率仍然很高。然而,除了少数互联网赌场外,无限牌堆只是一种抽象概念。我很好奇,如果在8副牌的游戏中,荷官一张牌都没发,只是说“你有16,我有10,但没有黑杰克”,那么最佳玩法是什么?使用 gamblingtools.net(网站已不存在)上的黑杰克分析器,我输入了8副牌,然后小心翼翼地把牌堆里的所有牌都抽光,除了没有6和2张10。然后我给了庄家一张10,我自己也给了10和6。所以玩家这手牌是用来对抗一副中性牌的,这副牌有31张A-9牌,还有124张10。预期值如下:
10+6 vs 10 — 八副牌
| 玩 | 预期价值 |
|---|---|
| 站立 | -0.5399 |
| 打 | -0.5399 |
虽然预期值数字相同,但小程序会强调停牌是更好的玩法,大概是因为停牌比小数点后四位更高。如果我删除以下数字:A、2、3、4、5、6、8、10、10、10,以模拟 9、7 对 10,结果也一样,因为玩家使用的是完全相同的中性牌盒。
这表明即使在八副牌的游戏中只有三张牌,移除的效果也有多么强大。回到最初的问题,在计算完玩家的两张牌和庄家的明牌后,零点数反映的是一副完全中性的牌。所以正如我刚才所展示的,进入中性牌堆后,停牌的几率更大。在无限牌堆中,要牌是正确的,因为没有移除的效果。如果你在中性牌盒中意外击中 16 对 10,并拿到一张小牌,那么庄家就有更大的机会拿到底牌 10。这一事实反映在八副牌游戏中停牌的预期值更高,但在无限牌堆中无关紧要。以下是无限牌堆游戏中的预期值:
10+6 vs 10 — 无限卡组
| 玩 | 预期价值 |
|---|---|
| 站立 | -0.5404 |
| 打 | -0.5398 |
二十一点游戏中,庄家有时会亮出底牌。在这种情况下,正确的基本策略是什么?
斯坦福·黄(Stanford Wong)在其著作《基础二十一点》(Basic Blackjack)中给出了这样的基本策略,见表46。他还提到,1995年拉斯维加斯波旁街赌场(Bourbon Street casino)曾推出一项促销活动,每50分钟,荷官会亮出自己的两张牌,持续五手。据黄称,在此期间,玩家的优势约为10%。
拆分后我应该使用您的基本策略例外吗?
这是个好问题。我个人会根据已经打出的牌,尤其是第二手牌的情况来判断边缘打法。如果非要我这么做,我会说使用例外策略比只使用基本策略更好。然而,基本策略的例外策略仅适用于第一手牌,因此它们对于分牌来说并不完全准确,因为牌组的构成会略有不同。
我猜你的二十一点策略是针对初始牌(玩家的前两张牌和庄家的明牌)的基本策略。但是,在拿牌或分牌之后,牌组构成发生了变化,基本策略也可能随之改变。我认为更合适的是基于二十一点整体游戏的基本策略,包括分牌和拿牌之后的基本策略。你的初始牌基本策略和整体游戏的基本策略是否存在差异?
是的,我的基本策略图表旨在根据前两张牌确定最佳玩法。这是制定基本策略的常用方法。这种方法的一个好处是可以精确计算每种玩法的预期值并与其他来源进行比较。但是,你提出的观点很有道理。因此,我询问了《Blackjack Attack》的作者唐·施莱辛格,是否存在任何已知的玩法,其中初始手牌的最佳玩法不同于最大化整个二十一点游戏的预期值的最佳玩法。他回答说,在双层牌游戏中,软 18 对抗庄家的 A,而庄家在软 17 点停牌,就是这样一种玩法。正如我的二十一点附录 9所示,停牌的预期值为 -0.100502,要牌的预期值为 -0.100359。因此,基于前两张牌,要牌的赔率为 0.000143。但是,看到软 18 的方式远不止一张 A 和一张 7。下表显示了这手牌可能出现的所有方式。
Soft 18 与 Ace 组合分析
| 玩家 牌 | 条件 可能性 | 打 电动汽车 | 站立 电动汽车 | 打 返回 | 站立 返回 |
| A7 | 0.621139169 | -0.100359 | -0.100502 | -0.062336906 | -0.062425729 |
| A6A | 0.036728229 | -0.11202 | -0.116009 | -0.004114296 | -0.004260805 |
| A52 | 0.146912917 | -0.111299 | -0.103382 | -0.016351261 | -0.015188151 |
| A43 | 0.146912917 | -0.114804 | -0.103721 | -0.01686619 | -0.015237955 |
| A5AA | 0.001827682 | -0.111395 | -0.105122 | -0.000203595 | -0.00019213 |
| A42A | 0.016814677 | -0.116975 | -0.108233 | -0.001966897 | -0.001819903 |
| A33A | 0.007356421 | -0.132142 | -0.107256 | -0.000972092 | -0.00078902 |
| A322 | 0.020470041 | -0.134229 | -0.11004 | -0.002747673 | -0.002252523 |
| A4AAA | 0.000073486 | -0.117554 | -0.110984 | -0.000008639 | -0.000008156 |
| A32AA | 0.001028802 | -0.134775 | -0.112433 | -0.000138657 | -0.000115671 |
| A222A | 0.000709873 | -0.136788 | -0.114993 | -0.000097102 | -0.00008163 |
| A3AAAA | 0.000002238 | -0.135313 | -0.114821 | -0.000000303 | -0.000000257 |
| A22AAA | 0.000023502 | -0.137312 | -0.117376 | -0.000003227 | -0.000002759 |
| A2AAAAA | 0.000000046 | -0.137859 | -0.119823 | -0.000000006 | -0.000000006 |
| 全部的 | 1 | -0.105806844 | -0.102374694 |
列标题说明
玩家卡:玩家手中的牌
条件概率:假设玩家拥有软 18 点,而庄家拥有 A 点,则给定手牌组成的概率。
Hit EV:击中后的期望值
站立EV:站立的预期值
命中回报:概率与命中预期值的乘积
林分回报:概率与林分期望值的乘积
底行右侧两个单元格显示,击球的总体预期值为 -0.105807,停球的总体预期值为 -0.102375。因此,表格显示停球的赔率为 0.00343。
为了验证这些结果,我根据相关规则进行了两次模拟,一次模拟要牌,一次模拟停牌。我只统计了在游戏过程中出现软18对抗庄家A的牌局。以下是我的结果。
软18对Ace模拟
| 软 17 | 手 播放次数 | 全部的 赢 | 预期的 价值 |
| 站立 | 3857490 | -396224 | -0.102715 |
| 打 | 3208390 | -337572 | -0.105215 |
因此,模拟结果显示,在所有可能出现这手牌的情况下,停牌的概率为0.0025。因此,从实际玩所有牌的角度考虑,最佳玩法是停牌,这与我的基本策略图所示相反。
您好。我刚刚偶然发现了您的网站,我觉得这是一个非常棒的二十一点信息网站。不过我有个问题。您能解释一下,当您遵循基本策略,并且总牌点数为10,而庄家明牌为10或A(庄家没有黑杰克)时,为什么会有正期望值吗?您的表格显示了这两种情况下的正期望值,但我不明白是怎么回事。我认为在这种情况下,玩家和庄家遵循相同的策略,即要牌直到17点或更高,否则爆牌。在这种情况下,玩家的软17点会被淘汰,所以我不明白正期望值从何而来。
感谢您的赞美。假设有六副牌(庄家在软17点时要牌或停牌都无所谓)。我的二十一点附录9显示,6+4对A的预期值为+0.081336,6+4对10的预期值为+0.026796。预期值为正的原因是,我的预期值表假设庄家已经偷看过黑杰克,并确认自己没有。与此同时,玩家仍然可以抽到一张A,凑成21点。换句话说,玩家可以在下一张牌凑成21点,而庄家不能,这是假设。如果我有一张符合欧洲不偷看规则的预期值表,那么预期值确实会是负数。
我最近去拉斯维加斯的时候,看到两个独立的荷官(一个在奥尔良赌场,一个在马戏团赌场)建议在4-4对6时加倍而不是分牌。我是我们这群人里最擅长“双倍”的荷官,所以我的朋友们开始问我这个问题。我只能说:不,分牌是正确的决定。(当然,前提是允许分牌后加倍。)请问这两种选择的可能性是多少,或者您能告诉我吗?此致
我以前说过,虽然我很尊重庄家,但他们也给出了很多糟糕的建议和错误信息。用四对五或六分牌是一种常见的玩法,玩家和庄家都会错误地反对分牌。有时你会听到有人错误地说,你永远不应该分“任何以F开头的牌”,也就是四、五和人头牌。对于五和人头牌来说,这话没错,但如果允许分牌后加倍,玩家确实应该用四对五或六分牌。否则,玩家应该要牌,除非在单副牌游戏中,如果允许加倍,他应该要牌。我的二十一点附录9显示,在六副牌游戏中,庄家拿到软17,对6的预期值为4和4。
立场:-0.114085
命中:+ 0.113365
双精度:+ 0.092929
拆分:+0.207228(允许拆分后加倍)
拆分:+ 0.056954(拆分后不允许加倍)
巫师,我一直在浏览您的网站,准备去拉斯维加斯玩一趟,因为它是目前最好的赌博网站。您在2001年12月4日的专栏文章中,分析了16点对庄家10点的持牌时机,这让我很感兴趣。作为一个数学爱好者,我希望最大化胜算,但同时也明白微薄的收益。和许多玩基础策略的玩家一样,当我手上有2、3、4或5点时,我总是能拿到16点对庄家10点。我很好奇,自从你注意到这个问题后,你是否调整了你的玩法,以达到“每5年赢一个单位”的目标,还是坚持每次都拿到16点?谢谢你!
谢谢你的赞美。如果我玩的是基本策略(而不是算牌),如果我手上已经有4或5,我通常会停牌。如果是明牌游戏,有其他玩家,我会环顾牌桌,然后根据自己的判断来决定。
在二十一点游戏中,庄家会亮出两张牌(附录 16 ),当庄家的点数为 10 或 11 时,一对 8 不会进行分牌;相反,庄家的点数为 10 时,要牌;当庄家的点数为 11 时,要停。这和常规的 BS 不同,常规的 BS 是将 8 与庄家的 10 或 A 分牌。
在常规二十一点游戏中,玩家确实应该在庄家拿到10或A时分牌。但是,如果庄家不小心翻开两张牌,总点数为10或11,玩家应该在10时要牌,在11时停牌。这是因为,当庄家拿到10或A时,轮到你时,你就知道庄家没有黑杰克,因为他会偷看底牌确认。所以你可以更积极地出牌。但是,当庄家的两张牌都翻开,总点数为10或11时,庄家肯定可以拿到一张A对应10,或者一张10对应11,总点数为21,所以在这种情况下,你应该采取更保守的策略。
在二十一点的“牌移除效果”中,移除小于5或4的6的效果……是这样吗?(我以为6是最佳移除点数,或者非常接近5,是最佳移除点数)。谢谢
我觉得你把取牌和庄家的明牌搞混了。下表显示的是玩家仅根据庄家的明牌,在庄家检查是否有黑杰克之前,根据庄家的明牌获得的预期值,假设庄家在软17点和无限牌上停牌。
庄家明牌的预期值
| 明牌 | 预期的 价值 |
| 2 | 9.10% |
| 3 | 12.38% |
| 4 | 15.85% |
| 5 | 19.65% |
| 6 | 23.40% |
| 7 | 14.40% |
| 8 | 5.82% |
| 9 | -4.06% |
| 10 | -17.36% |
| 一个 | -33.78% |
所以,如果可以为庄家选择一张明牌,那应该选六,这确实是事实。六对庄家不利,但对玩家也不利。综合考虑,如果可以从牌盒中取出一张牌,应该选五。
很棒的网站!你的二十一点策略卡是我见过最好的。哪里有卖的?我现在用的那个没有投降选项,用这个会有什么损失吗?
谢谢。几乎每家赌场礼品店都会出售基本的策略卡,但不知为何,他们没有标明何时应该投降。投降的情况并不多,但这些情况经常发生,所以我认为值得记住。在六副牌的游戏中,如果庄家拿到软17点停牌,投降概率为0.07%,如果拿到软17点,投降概率为0.09%。
我和朋友在拉斯维加斯玩牌。我们大吵了一架,争论的是,在两副牌的游戏中,玩家总点数10,庄家点数7,双倍下注,还是玩家总点数11,庄家点数10,双倍下注,哪个从统计上看赔率更高。我以为是前者。
我的二十一点附录9就是为这类问题设计的。假设有6副牌,我的表格显示,8+2对7的加倍预期值为0.396342。8+3对10的加倍预期值为0.176919。所以你说得对,10对7的加倍是更好的选择。
根据标准 BJ 规则和完美的基本策略,我预计我的 DOUBLED DOWN 牌会赢、推和输的百分比是多少?
假设拉斯维加斯大道的规则较为宽松(六副牌,庄家在软17点停牌,分牌后允许加倍,允许后期投降,允许再次分牌A),以下是最初两张牌加倍时各种可能结果的概率。这不包括分牌后加倍。
我有个朋友,当他第一张牌是6时就开始抱怨,根本没等看第二张牌和庄家的明牌是什么。我觉得他应该等等,因为他可能拿到2、3、4、5等等(也就是一张不错的第二张牌),或者庄家也可能亮出2到6(一张好牌)。你怎么看?如果第一张牌是6,而他不知道第二张牌或庄家的明牌是什么,他的赢钱概率会降低多少?还是我的朋友只是个爱抱怨的人?谢谢你抽出时间。
我的二十一点附录14显示,如果你的第一张牌是6,你的预期价值就已经约为-21%。例如,如果他下注100美元,那么卖出这手牌并下注的合理价格大约是79美元。或许你可以利用他的抱怨,提出以低于79美分的合理价格买下他的牌。我建议75美分的出价,这样既能给你带来优势,又不会占太多便宜。
上周末我玩二十一点的时候遇到过这种情况,庄家明牌是6,但他在收底牌的时候,不小心亮出了3。我右边的玩家是15,我是11,左边的玩家是12。我右边的玩家知道庄家的总牌数是9,于是他要了一张10,爆牌了。我最后加倍下注,拿到了2。左边的玩家要了一张5,总牌数是17。庄家开牌是9,要了一张10,总牌数是19。庄家告诉我们,即使你看到了小3,也应该像不知道底牌一样出牌。我想问一下,如果当时三位玩家都遇到这种情况,你会怎么做。自从我玩二十一点以来,这种情况还是第一次发生。请指教。谢谢!
我的闪光二十一点庄家策略展示了在庄家意外暴露底牌的情况下该如何应对。然而,大多数玩家,包括我,都没有记住这一点。在这种情况下,如果庄家的两张牌总点数不超过九点,你可以使用基本策略,假设庄家的明牌等于他两张牌的总和。根据这个经验法则,三位玩家都玩得正确。与庄家的说法相反,玩家完全有权利用从此类庄家错误中收集到的任何信息。我不仅会无视庄家的评论,还会继续玩,希望他再次犯错。
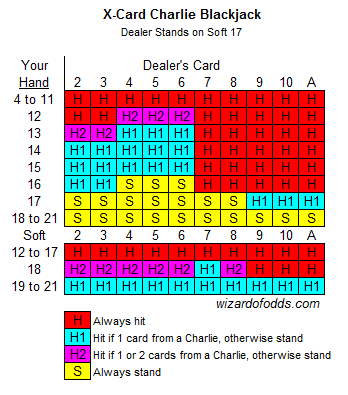
感谢您创建了一个很棒的网站,提供如此详尽的信息。您提到了二十一点中各种查理牌的庄家优势显著降低,但我没有看到任何关于不同玩法的建议。在大型(6副以上)牌盒中,有没有什么值得利用的基本策略例外来最大化利润?我猜想,如果庄家爆牌的可能性很小,那么如果离查理牌只有一张牌,那么你应该会拿到更多牌,但我希望看到具体的说明。谢谢。
不客气。对于那些可能不明白这个问题的读者,“查理”规则是指玩家只要拿到一定数量的牌(通常是五到七张)且没有爆牌,就自动获胜。下表针对三张或三张以上的牌,展示了当玩家距离这种自动获胜者只差一两张牌时的基本策略。
许多赌场允许在二十一点牌桌上,玩家在后方下注。请问,假设两位玩家联手下注,当“后方”下注金额远超常规下注金额时,正确的分牌策略是什么?
希望您满意,我添加了一个新页面来回答这个问题。请参阅我的“二十一点附录 19” 。
我研究并使用了你的二十一点附录16 (庄家揭底牌策略)已经有一段时间了,但仍然有一个玩法我找不到数学解释:A2 vs. 5。基本策略会将此视为加倍,并且使用你自己的“牌移除效应”数字,当你手上有软13时,从牌堆中移除2和3应该会让牌堆对玩家更有利,而不是更不利。我为什么没看到?
原因是我的二十一点基本策略基于8副或更少的牌,而闪牌庄家策略则基于无限多副牌。在无限副牌的二十一点游戏中,你也应该打出A2而不是5。无限副牌假设是分析二十一点的偷懒方法。我之所以这样做,是因为我认为这个页面不常用,而且错误成本非常低,每202,000个单位的赌注只犯一个单位的错误。
我觉得我注意到你跟一个21点后下注的玩家分牌策略有个错误。它说,如果你的后下注玩家分牌是10对8(这是自私的牌表),你只能玩一手牌。但是,硬10(没有加倍)对8仍然有正的预期价值。
原因是我的表格假设前排玩家会继续重新分牌(如果可以的话)。这会降低单张10的价值,因为我假设前排玩家会继续犯同样的错误(如果可以的话)。我刚刚把这个条件添加到了那个页面。
感谢您提供详细的网站。在二十一点附录9中,您列出了游戏的预期值以及每种玩法的预期值。我预计游戏的预期值是E i × P i之和,其中E i是第i种玩法(停牌/要牌/加倍/分牌)的最大预期值,P i是第i种玩法的概率。当我尝试进行此计算时,得到了不同的结果。例如,六副牌,庄家在软17点要牌,玩家在分牌后不得加倍,我得到的结果是0.04518876。
这些表格假设庄家没有黑杰克。这是因为轮到玩家行动时,庄家已经偷看了黑杰克。假设庄家没有黑杰克,正确的加倍或分牌决策应该基于条件期望值。否则,玩家面对10或A时,会过于胆怯,不敢加倍或分牌。将概率和期望值的点积相加会得出错误的结果,因为庄家拿到黑杰克时,并没有损失。
要计算整个游戏的赌场优势,你应该减去庄家拿到黑杰克时的预期损失。如果是六副牌,庄家拿到黑杰克的概率是10的数量乘以A的数量,再除以两张牌组合的数量,即 (6×16)×(6×4)/combin(312,2) = 0.047489。然而,玩家只有在没有黑杰克时才会输。假设庄家已经有一张黑杰克,玩家拿到黑杰克的概率是 (6×16-1)×(6×4-1)/combin(310,2) = 0.045621。因此,玩家输给庄家黑杰克的概率是 0.047489 × (1-0.045621) = 0.045323。你应该从上面的点积中减去这个数字:0.04518876 - 0.045323 = -0.00615144。因此,根据附录中规定的规则,赌场优势为0.62%。
我 100% 的时间都遵循您的 4+ 副牌二十一点基本策略,每当我拿到 12 点而庄家拿到 2 点,尤其是 3 点时,我总是会遭到鄙视。我不知道如何用简单的术语向其他玩家解释为什么我所做的是最好的事情。
我感同身受。你可以想象西班牙21点有多糟糕,它要求玩家像3点对14点这样的打法。如果只是表面现象,我就会放过它。如果只是文字问题,我会说:“这里还有很多其他桌子。”你根本无法用解释赔率来说服这种傻瓜。信念越荒谬,人们就越容易固执己见。
无论如何,通常没有简明扼要的解释来解释为什么一种玩法比另一种更好。要知道为什么正确的玩法是那样,你必须要么考虑剩余牌可能出现的所有情况,无论是玩家还是庄家,要么把这手牌玩上千遍,甚至数百万遍,直到牌局非常边缘化。你应该选择预期价值最高的那个。只有拒绝保险的玩法才容易解释。
我知道图表上是怎么说的,但在二十一点中,如果庄家有9、10或A,我没法让自己用8分牌来对抗他。我的问题是,这会对赌场优势造成什么影响?
假设有六副牌,庄家在软17点停牌,玩家可以重新分牌,最多分到四手牌。每次基本策略变化的影响在于该手牌出现的概率以及出现错误打法的成本。我的二十一点附录9显示了每手牌出现的概率以及每种打法的预期价值。假设玩家选择要牌而不是分牌,对游戏预期价值的影响如下:
概率(8,8 vs A)×(EV(击中)-EV(拆分)) + 概率(8,8 vs 9)×(EV(击中)-EV(拆分)) + 概率(8,8 vs 10)×(EV(击中)-EV(拆分))
= 0.0003036 × (-0.513551 -(-0.364371)) + 0.0004404 × (-0.505707 -(-0.38995)) + 0.0016249 × (0.535361 -(-0. 475385))
= -0.019%。
因此,如果庄家拿到 9、10 或 A,而玩家拿到 8、8,赌场优势就会增加 0.019%,也就是说,每玩 5,300 手牌,赌场优势就会增加一次。如果玩家选择投降而不是拿牌,赌场优势就会降至 0.013%。所以,这并不是一个重大错误。相比之下,在六副牌的游戏中,如果玩家拿到“等额赌注”,而庄家拿到 A,赌场优势就会增加 0.014%。如果玩家对每张黑杰克和 20 都投保(这是一个常见的错误),那么错误成本就会跃升至 0.149%!
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
不久前,我在拉斯维加斯大道上的一家赌场玩6-5的二十一点,当时我喝了不少免费酒,结果每次庄家2-6,我拿到二十一点,就加倍下注。幸运的是,我每次都赢了。但是,我琢磨着我的决定到底有多糟糕。如果二十一点的赔率是1比1,那还合理吗?
我的二十一点附录9可以解答这类问题。例如,假设有六副牌,庄家拿到软17,那么用二十一点对抗庄家5点加倍的预期价值为0.622136,对抗庄家6点加倍的预期价值为0.667063。两者均远低于1.2,成本超过一半的赌注。即使二十一点只支付等额的赌注(不幸的是,现在有时确实如此),你也应该在二十一点上停牌。唯一不应该在二十一点上停牌的游戏是三倍21点,玩家在二十一点对抗庄家6点上应该三倍下注。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
你的二十一点基本策略表是基于最大化每手牌的预期价值。然而,是否存在这样的情况:加倍或分牌比要牌或停牌略微糟糕,以至于错误成本低于额外玩一手牌的赌场优势?
是的!让我们考虑以下情况:
6层甲板
庄家拿到软 17
玩家有 A,6
庄家亮出 2
根据我的二十一点附录 9 ,以下是每次玩法的预期值:
立场 -0.152739
命中 -0.000274
双倍 -0.004882
因此,要牌是平均输钱最少的玩法。如果玩家加倍,该误差的预期值为 -0.004882 - (-0.000274) = -0.004608。根据我的二十一点庄家优势计算器,在这些规则下(假设投降、分牌后加倍以及A重新分牌),庄家优势为 0.48%。通常情况下,某些选项是不允许的,从而增加了庄家优势。因此,只要庄家在六副牌的游戏中拿到软 17,那么在面对 2 时将软 17 加倍的成本低于在另一手牌上下注相同金额的成本。
在任何涉及加注的游戏中,你都可以提出同样的观点。例如,在三张牌扑克中,如果你想最小化每手牌的预期损失,那么最佳策略是在Q64或更高牌面加注,正如我在三张牌扑克页面上所提到的。然而,如果你的目标是最小化每手牌总投注额的预期损失,那么最佳策略是在Q62或更高牌面加注。
这就引出了一个问题:为什么像我这样的赌博作家会以最小化每注初始投注的预期损失而不是总投注金额作为策略基础?我的答案是,这主要是出于传统。二十一点基本策略就是这样诞生的,出于习惯和简便性,每个人都保留了这种方法。如果休闲玩家的目标是在规定的时间内最小化损失,那么他应该采用能够最小化每手牌预期损失的传统策略。如果玩家的目标是最小化总投注金额超过 x 美元的损失,那么他应该选择前面提到的那种略微糟糕的加倍和加注策略。我倾向于认为大多数玩家的目标都是基于时间的,因此更倾向于采用传统策略。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
我知道很多二十一点玩家不喜欢在面对9、10或A时用8分牌。你认为这种玩法是最常犯的错误吗?如果不是,你认为是什么?
我认为二十一点玩家最容易犯错的玩法是在允许分牌后加倍的情况下,对着5或6分牌,却用4、4分牌。在六副牌的游戏中,出现这种情况的概率是1/1135。根据我的二十一点附录9 ,假设玩家选择要牌而不是分牌,那么对着5的预期成本是2.83%,对着6的预期成本是4.38%。总的来说,如果玩家每次都犯这个错误,游戏的庄家优势就会上升0.0032%。所以,这个错误代价不高,因为它很少发生。然而,我从未见过其他玩家在这种情况下正确地分牌。当我看到的时候,荷官和其他玩家通常会翻白眼。有一次,我听到另一个玩家假装我不在场,错误地对荷官说:“你永远不应该分任何以F开头的牌。”
如果问题是,考虑到玩牌频率和错误代价,哪个错误代价最大,那么我只能大胆猜测一下。我的猜测是,最大的错误是没有在应该软加倍的时候软加倍。我很少看到业余玩家用软17对6这样的牌加倍。下表显示了四种常见错误导致的赌场优势的增加。该表假设玩家在这种情况发生时总是犯错误,而不是选择次优选择。例如,在12对2或3的情况下停牌,我没有将6、6的玩家纳入考虑。
常见的二十一点错误
| 错误 | 可能性 | 每次事故的平均成本 | 每手成本 |
|---|---|---|---|
| 绝不软双 | 0.016430 | 0.054357 | 0.000893 |
| 12 点对 2 点或 3 点时停牌 | 0.000380 | 0.029955 | 0.000380 |
| 软 18 号牌对 9-A 号牌停牌 | 0.000205 | 0.041605 | 0.000205 |
| 击中 8,8 对抗 9-A | 0.000194 | 0.081779 | 0.000194 |
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
为什么基本策略说16比10要牌,而Hi-Lo点数却说点数大于或等于零就停牌?基本策略不是基于满牌,也就是点数为零吗?看来两种策略都不可能正确。
首先,值得重申的是,16对10的牌局是一手介于要牌和停牌之间的牌。如果允许投降,那么对于采用基本策略的玩家来说,这比要牌或停牌要好得多。否则,平均而言,要牌会稍微好一点。只需从八副牌的牌盒中取出一张小牌,就能改变停牌的赔率,因为少了一张小牌,剩下的大牌就更多了,要牌的风险也就更大了。这就是为什么我说,如果你的16点由三张或更多牌组成,你就应该停牌,因为一张三张16点通常会从牌盒中取出至少两张小牌。
其次,洗牌后的第一手牌,如果基本策略和算牌策略在如何玩这手牌上有所不同,则以基本策略为准。基本策略是根据观察到的具体牌型精心设计的,旨在考虑牌堆的具体构成。索引值表是一种更直观的工具,适用于所有牌盒。
在这种特殊情况下,算牌者可以选择要牌或停牌,这取决于他如何对真实点数进行舍入。如果他向下舍入,真实点数将为 -1,因此他要牌。如果他向上舍入,即舍入到最接近的整数,则真实点数将为 0,因此他停牌。只要我提到这一点,根据唐·施莱辛格 (Don Schlesinger) 的《黑杰克攻击》(Blackjack Attack),舍入的首选方法是“向下取整”,即向下舍入,在本例中为 -1,因此玩家可以正确要牌。
另一个类似的情况是 15 对 10。83% 的时间(10+5 或 8+7,但不是 9+6),这会导致洗牌后第一手牌的运行计数为 -1,而投降的索引号为 0。向下舍入会导致玩家错误地击中,而投降是更好的选择。
底线是,洗牌后第一次做决定时,如果其他玩家没有其他牌,算牌者应该使用基本策略。之后,恢复使用索引号。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。


