请问巫师 #321
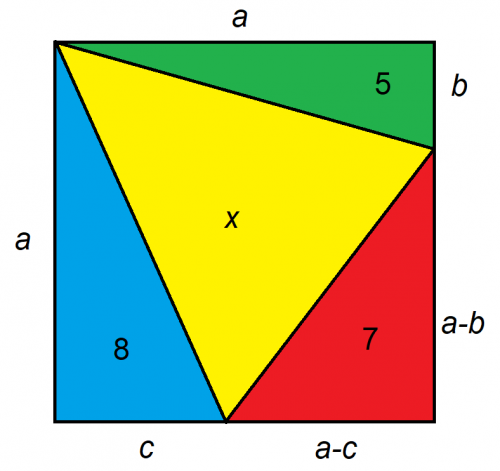
假设较大的图形是正方形,x 的面积是多少?
解决这类问题的关键在于如何设置它们。我建议尽量将问题简化为尽可能少的未知数。在本例中,我们可以将正方形上的未知距离表示为三个,如下所示:
处理矩形比处理三角形更容易。已知三个三角形的面积,我们可以将矩形的大小和面积都加倍。这样一来:
- ab=10
- ac=16
- (ab)(ac)=14
让我们分解 (ab)(ac):
a 2 - ab - ac + bc = 14
2-10-16 + bc = 14
(1) a2 +bc=40
让我们用 a 来表示 b 和 c,以将其归结为单个变量:
b = 10/a
c = 16/a
用这些值代替方程 (1) 中的 b 和 c:
2 + (10/a)*(16/a) = 40
a2 + 160/ a2 = 18
接下来,让我们将所有数都乘以2来去掉分母中的2 。
4 + 160 = 40 * 2
4-40 * 2 +160=0
让我们定义一个新变量 y = a 2
y 2 - 18y + 32 = 0
接下来,让我们使用二次公式求解 y:
y = (40 +/- 平方根(1600-640))/2
y = (40 +/- 平方根(960))/2
y = (40 +/- 8*sqrt(15))/2
y = 20 +/- 4 * sqrt(15)
整个正方形的面积是2 ,恰好等于 y。根据上面的公式,如果 +/- 为负,则 y = apx 4.5081,这显然是错误的,因为我们知道面积至少是 20,甚至不包括 x。因此,正方形的面积必须是 20 + 4*sqrt(15)。
给定三个三角形,其面积分别为 5+7+8=20。用正方形的总面积减去该面积,可得出 x 的面积:20 + 4*sqrt(15) - 20 = 4*sqrt(15) = apx 15.4919。
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。

注意照片里我的T恤。我去看《原钻》的时候,电影院收银员夸我穿了这件T恤。为了报答她,我用这道题折磨她,只用面积分别为2、3和4的三角形。电影结束后,我去看她,她还是没解出来,但似乎在努力。于是,我在阳光海岸酒吧给她写了下面的解法。她似乎很欣赏。我觉得这位年轻女士的人生一定会很成功。
关于彩票,在跨州彩票(强力球、超级百万)中,是否存在一个“临界点”,即大奖被分割的可能性大于最终只有一个中奖者的可能性?如果存在,这个“临界点”是多少?
我不会深入讨论所有的数学问题,但以下是多个获胜者与只有一个获胜者的可能性相同的累积奖金点:
- 强力球:9.75亿美元
- 超级百万:16.5亿美元
并不是您问的,但这里列出的是至少有一个获胜者的概率等于没有获胜者的概率(50%)。
- 强力球:7.04亿美元
- 超级百万:8.67亿美元
这个问题是在我的“拉斯维加斯巫师”论坛中讨论过的。
- 监狱里有12名囚犯,每人编号为1到12。
- 监狱长设置了12个箱子,每个箱子编号为1到12。
- 12 个盒子里面是数字 1 到 12,随机放置,每个盒子一个。
- 每名囚犯每次可自行选择开启六个箱子。囚犯每次可选择一个开启。
- 每个囚犯的目标是在六个选择框中找到自己的号码。如果找到了,则该人存活。
- 如果一名囚犯找不到自己的号码,那么整个团队就被认为失败了,他们会立即被带到行刑队。
- 如果一名囚犯幸存下来,那么他必须将数字放回原来的盒子中,以便下一个囚犯使用。
- 游戏开始后,囚犯不得观看其他玩家或进行交流。
- 开始之前,全组成员需要共同制定一个策略。目标是12名囚犯全部存活下来(也就是在盒子里找到自己的号码)。
他们的策略应该是什么来最大限度地提高生存概率,这个概率是多少?
[剧透=解决方案]
就像“秘密圣诞老人”游戏一样,游戏中会有从一个数字到另一个数字的循环。如果有12名囚犯,循环的个数可以是1到12个。如果没有循环大于6,那么每个囚犯最终都会找到自己的数字。最大的问题是,没有循环大于6的概率是多少?让我们反过来算一下,找出循环大小为7或更大的组合数。
12囚徒解决方案
| 循环 | 组合 | 可能性 |
|---|---|---|
| 12 | 39,916,800 | 0.083333 |
| 11,1 | 43,545,600 | 0.090909 |
| 10,2 | 23,950,080 | 0.050000 |
| 10,1,1 | 23,950,080 | 0.050000 |
| 9,3 | 17,740,800 | 0.037037 |
| 9,2,1 | 26,611,200 | 0.055556 |
| 9,1,1,1 | 8,870,400 | 0.018519 |
| 8,4 | 14,968,800 | 0.031250 |
| 8,3,1 | 19,958,400 | 0.041667 |
| 8,2,2 | 7,484,400 | 0.015625 |
| 8,2,1,1 | 14,968,800 | 0.031250 |
| 8,1,1,1,1 | 2,494,800 | 0.005208 |
| 7.5 | 13,685,760 | 0.028571 |
| 7,4,1 | 17,107,200 | 0.035714 |
| 7,3,2 | 11,404,800 | 0.023810 |
| 7,3,1,1 | 11,404,800 | 0.023810 |
| 7,2,2,1 | 8,553,600 | 0.017857 |
| 7,2,1,1,1 | 5,702,400 | 0.011905 |
| 7,1,1,1,1,1 | 570,240 | 0.001190 |
| 全部的 | 312,888,960 | 0.653211 |
下表显示了上表中组合的公式。
组合配方
| 循环 | 组合 | 公式 |
|---|---|---|
| 12 | 39916800 | =事实(11) |
| 11,1 | 43545600 | =组合(12,11)*事实(10) |
| 10,2 | 23950080 | =组合(12,10)*事实(9) |
| 10,1,1 | 23950080 | =组合(12,10)*事实(9) |
| 9,3 | 17740800 | =组合(12,9)*事实(8)*事实(2) |
| 9,2,1 | 26611200 | =组合(12,9)*组合(3,2)*事实(8) |
| 9,1,1,1 | 8870400 | =组合(12,9)*事实(8) |
| 8,4 | 14968800 | =组合(12,8)*事实(7)*事实(3) |
| 8,3,1 | 19958400 | =组合(12,8)*组合(4,3)*事实(7)*事实(2) |
| 8,2,2 | 7484400 | =组合(12,8)*组合(4,2)*事实(7)/2 |
| 8,2,1,1 | 14968800 | =组合(12,8)*组合(4,2)*事实(7) |
| 8,1,1,1,1 | 2494800 | =组合(12,8)*事实(7) |
| 7.5 | 13685760 | =组合(12,7)*事实(6)*事实(4) |
| 7,4,1 | 17107200 | =组合(12,7)*5*事实(6)*事实(3) |
| 7,3,2 | 11404800 | =组合(12,7)*组合(5,3)*事实(6)*事实(2) |
| 7,3,1,1 | 11404800 | =组合(12,7)*组合(5,3)*事实(6)*事实(2) |
| 7,2,2,1 | 8553600 | =组合(12,7)*组合(5,2)*组合(3,2)*事实(6)/2 |
| 7,2,1,1,1 | 5702400 | =组合(12,7)*组合(5,2)*事实(6) |
| 7,1,1,1,1,1 | 570240 | =组合(12,7)*事实(6) |
从第一个表格的右下角单元格开始,共有 312,888,960 种输的组合。这些数字的排列方式总数为 12! = 479,001,600。因此,失败的概率为 312,888,960 / 479,001,600 = 65.32%。因此,成功的概率为 100% - 65.32% = 34.68%。
[/spoiler]这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
您好。我有一张优惠券,可以让我把22点的牌推下去。我可以保留这张优惠券直到我拿到第一个22点。这张优惠券不适用于加倍或分牌。这张优惠券的价值是多少?
答案很简单,就是你允许下注的最高金额。等到22点,再玩,最后就能带着一个额外的单位离开赌桌。
更严格的答案应该考虑等待这 22 的成本。这是我并不确切知道的,但可以估计。
庄家“全压22”规则对玩家的成本为6.91%。然而,庄家拿到22点的概率会高于这个数字,因为玩家不在乎自己是否先爆牌。根据规则,玩家爆牌的概率约为15.7%。如果我们假设这与庄家爆牌的概率无关(事实并非如此),那么庄家爆牌的概率为6.91%/(1.0-0.157) = 8.2%。
我知道这有点粗略,但我们假设玩家拿到22点的概率相同。我知道庄家爆牌的概率比玩家高,但分牌后这张优惠券也不算数,所以我们就假设这些因素互相抵消了。所以,如果玩家拿到22点的概率是8.2%,那么他平均每1/0.082 = 12.2手牌就会拿到一次22点。
假设基础游戏中的赌场优势为0.75%。以该赌场优势玩12.2手牌的成本为12.2*0.0075 = 0.0915。因此,用一个单位的价值减去这个成本,你得到的票面价值为1.0 - 0.0915,约为票面价值的91%。
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。