请问巫师 #318
假设玩家不知道奖品的价格,那么在“价格猜猜猜”游戏中玩竞赛游戏的最佳策略是什么?
为了让不熟悉该游戏的读者了解一下,这里有一个该游戏的视频。
我认为以下策略的平均回合数最低。有很多策略可以与之匹敌,但我认为没有哪个策略能超越它。
要使用该策略,请将四个价格标签标记为 1、2、3 和 4。根据您过去正确回答的问题的历史记录,从左侧的第一个转弯开始,将它们放在四个奖品上。
竞赛游戏策略
| 历史 | 一等奖 | 奖品二 | 三等奖 | 奖品 4 |
|---|---|---|---|---|
| 没有任何 | 1 | 2 | 3 | 4 |
| 0 | 2 | 1 | 4 | 3 |
| 0,0 | 3 | 4 | 2 | 1 |
| 0,0,0 | 4 | 3 | 1 | 2 |
| 0,0,2 | 3 | 4 | 1 | 2 |
| 0,0,2,0 | 4 | 3 | 2 | 1 |
| 0.2 | 2 | 3 | 4 | 1 |
| 0,2,0 | 4 | 1 | 2 | 3 |
| 0,2,1 | 2 | 4 | 1 | 3 |
| 0,2,1,0 | 3 | 1 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 1,0 | 2 | 4 | 3 | 1 |
| 1,0,0 | 3 | 1 | 2 | 4 |
| 1,0,0,0 | 4 | 2 | 1 | 3 |
| 1,1 | 1 | 4 | 2 | 3 |
| 1,1,0 | 2 | 3 | 1 | 4 |
| 1,1,0,0 | 3 | 2 | 4 | 1 |
| 1,1,0,0,0 | 4 | 1 | 3 | 2 |
| 2 | 2 | 1 | 3 | 4 |
| 2,0 | 1 | 2 | 4 | 3 |
| 2,1 | 1 | 3 | 2 | 4 |
| 2,1,0 | 4 | 2 | 3 | 1 |
| 2,1,1 | 1 | 4 | 3 | 2 |
| 2,1,1,0 | 3 | 2 | 1 | 4 |
下表显示了在 24 种可能的排列方式中,四个价格标签需要 1 到 5 次旋转的概率。
所需圈数
| 转弯 | 数字 | 可能性 |
|---|---|---|
| 1 | 1 | 4.17% |
| 2 | 4 | 16.67% |
| 3 | 8 | 33.33% |
| 4 | 9 | 37.50% |
| 5 | 2 | 8.33% |
| 全部的 | 24 | 100.00% |
取点积,该策略下所需的平均转数为 3.29167。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
在2019年9月18日播出的《危险边缘》节目中,有一个名为“描述赌场游戏”的环节。其中一条线索是“穿着得体,玩得尽兴;银行家的营业时间;邦德先生,您来摩纳哥是为了什么?”

答案是“百家乐”,并被判定为正确。邦德玩的不是二十一点吗?
是的,邦德玩的确实是二十一点,而不是百家乐。提醒一下,主要区别如下:
- 庄家轮流在牌桌上轮流发牌。庄家玩家自动获得庄家*牌。
- 玩家*和庄家都可以自由抽第三张牌,只要双方都没有两张自然牌 8 或 9。
笔记:
与往常一样,在撰写有关百家乐或二十一点的文章时,我会将赌注的名称大写,以避免与玩游戏的玩家混淆。
话虽如此,第一个这样的场景出现在下面的《诺博士》片段中,其中不仅银行旋转,玩家在第三张牌中拥有自由意志,而且邦德实际上在视频的 2:11 点口头上将游戏称为“chemin de fer”:
下一个视频展示了三部不同电影中的三个铁路场景。
以下是每个场景的起点:
- 2:09 — 雷霆万钧
- 4:19 — 女王密使
- 7:30 — 只为你的眼睛
在这三部电影中,我们都看到了玩家在第三张牌决策中采取的策略和自由意志,尤其是在《最高机密》中,讨论了赔率。
最后,下面是《黄金眼》中的场景。
这里我们再次看到了庄家轮次的来回切换以及抽第三张牌的自由选择。然而,在0:45处,女角色确实把这个游戏称为“百家乐”。我认为这是“角色错误”。
最后,毫无疑问,邦德在每部电影里都在玩二十一点。严格来说,我认为评委们接受“百家乐”作为正确答案是错误的。不过,我并不怪他们。即使按照《危险边缘》的标准,指望普通玩家区分百家乐和二十一点也太过分了。正如他们接受“The Mooch”而不是“Anthony Scaramucci”这样的答案一样,这表明评委们正在变得更加宽容。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
正如电影《贱女孩》中所问,什么是:
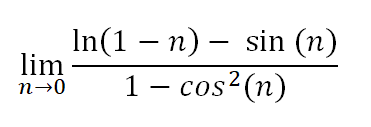
让我们首先查看 n(x 轴)乘以 f(n)(y 轴)的图表。
如你所见,极限从左边趋向于∞,从右边趋向于-∞。由于极限从两边不指向同一个位置,所以不存在极限。
不过,我们先不画图来回答这个问题。洛必达规则指出,如果 f(x)/g(x) 的极限 = 0/0,则 lim f(x)/g(x) = lim f'(x)/g'(x)。所以,我们来解 f'(x) 和 g'(x)。
f'(n) = ((ln(1-n) - sin(n)) d/dn = -1/(1-n) - cos(n)
g'(n) = (1 - cos 2 (n)) d/dn = sin 2 (n) d/dn
让我们用乘积法则来求解 sin 2 (n) d/dn
sin 2 (n) d/dn = sin(n) × sin(n) d/dn =
sin(n) × cos(n) + cos(n) × sin(n) =
2sin(n)cos(n)。
接下来,让我们求解 n = 0 时的 f'(n) 和 g'(n)。
f'(0)= -1/(1-0)-cos(0)= -2。
g'(0) = 2sin(0)cos(0) = 0
所以,f'(0)/g'(0) = -2/0 = -∞。因此,原函数的极限不存在。

我要夸赞《贱女孩》的编剧,他们把数学运用得炉火纯青。即使是像《心灵捕手》这样严肃的数学电影,也常常把数学运用得一塌糊涂。