请问巫师 #229
为了限制豪赌客带来的财务风险,您会建议赌场设定多大的最高赌注?我知道二十一点的数学庄家优势,但这并不能改变一个事实:如果赌注限额过高,大玩家很容易对赌场造成严重损失。
如果我经营一家赌场,我会运用凯利准则来设定最高赌注。我会将所有游戏的 m*v/h 设为均等值,其中 m 表示最高赌注,v 表示方差,h 表示赌场优势。我们称之为风险商。例如,假设我愿意在百家乐中押庄家 150,000 美元,这大约相当于拉斯维加斯大道上一家大型赌场的承受能力。赌场优势为 1.06%,方差为0.93 2。因此,风险商为 150,000*0.93 2 /0.0106 = 12,239,150。
接下来,我们来求 m 的值,以平衡二十一点中的风险商。在宽松的脱衣舞规则下,赌场优势为 0.29%。假设玩家最多可以下注三个点。给定三个下注点,每手牌的标准差为1.51957 ,因此方差为 1.51957 ² = 2.3091。求 m 的值……
米×2.3091/0.0029 = 12,239,150
米=15,371美元。
实际上,很少有玩家能完美运用基本策略,所以我可能会把这个数字提高到2万美元。这差不多就是拉斯维加斯大道上大型赌场在玩二十一点时能接受的金额,所以我认为这是合理的。我认为,对于新奇的游戏,他们应该接受更大的赌注。
我参加了一局在线扑克游戏,想知道发生这种情况的几率,请问:
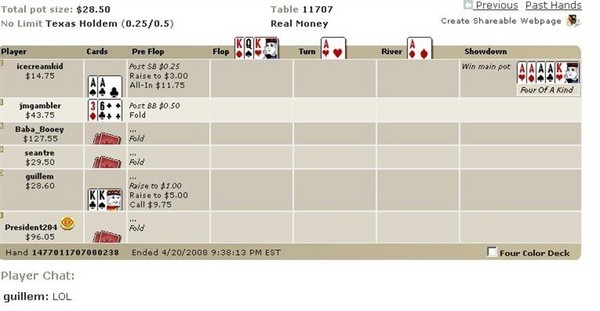
通常情况下,我厌倦了关于爆冷门(bad beat)的问题,但这道题实在太难了,我实在无法忽视。在一场双人游戏中,如果双方都有底牌对子,那么在第一张牌发出之前,四张K被四张A击败的概率是 2 * combin (4,2) * combin (4,2) * 44 / ( combin (52,2) * combin (50,2) * combin (48,5)) = 2 * 6 * 6 * 44 / ( 1326 * 1225 * 1712304) = 877,961,175 分之一。这是一场六人游戏,所以共有 combin (6,2) = 15 种不同的玩家对子。在六人游戏中,这个概率要高出 15 倍,即 58,530,745 分之一。发出所示底牌后,翻牌前,该手牌以原样结束的概率为 38,916 分之一。
您的牌九(骨牌)策略针对1997年2月发布的福克斯伍兹赌场规则(Foxwoods House Way)进行了优化。您的一些策略似乎存在玩家优势,或者接近均等的赔率。您是否知道拉斯维加斯或其他地方的赌场是否读过您的网站,并相应地调整了他们的赌场规则?您是否有更多关于不同赌场赌场规则的最新信息?另外,在您的牌九赔率表上,您有一个“最佳”策略,但我不清楚该策略的规则在哪里。什么是“最佳”策略?我非常喜欢玩这个游戏,并且正在寻找既能坚持玩下去,又能获得奖励,又不会损失太多钱的方法。
拉斯维加斯的凯撒宫在过去几年里改变了他们的规则。以前他们从不拆分“极品对”,现在却要拆分了。曼德勒海湾的一位荷官最近跟我提到了一项规则变更,规定玩0-7而不是3-4。至于这些变更背后的原因,我完全不知道。如果我能参与其中,我会感到自豪。
我最近为堪培拉赌场添加了一条房门。未来我可能还会为大西洋城的克拉里奇酒店和拉斯维加斯的金银岛酒店添加房门。把它们转换成HTML格式既繁琐又费时,所以我还没做这些。
我的助手JB正在研究针对福克斯伍兹主场的最佳策略。应该很快就会发布到网站上。
单张扑克游戏有三张牌,一张 A、一张 2 和一张 3。A 最小,3 最大。两位玩家各向底池下注 1 美元。然后,每位玩家拿到一张牌。下注顺序是预先确定的,玩家 1 先行动。玩家 1 可以下注 1 美元或过牌。如果玩家 1 下注,玩家 2 可以跟注或弃牌。如果玩家 1 过牌,那么玩家 2 可以下注 1 美元或过牌。如果玩家 1 过牌,玩家 2 下注,那么玩家 1 可以跟注或弃牌。如果两位玩家都过牌或都下注,那么牌值较大的玩家赢得底池。假设两位玩家都是完美的逻辑学家,那么每位玩家的最佳策略是什么?
希望你满意;我花了一整天时间研究这个问题。答案和解答可以在我的另一个网站mathproblems.info上的第 203 题找到,或者在 Jason Swanson 的学术论文《博弈论与扑克》中找到。


