请问巫师 #171
别再纠结你的NIM游戏了!我一直以为获胜的关键在于让你的对手(这里指的是计算机)留下的点数加起来等于下一个最小数字,这个数字等于它的二进制总和。也就是说,如果我有17个点,我取2个,剩下15个,也就是二进制数1、2、4、8的总和。但这似乎行不通。我是对还是错?
你在二进制数上的思路没错,但这并非真正的制胜策略。首先,如果你能让对手留下奇数行,每行一个,那就这样做。否则,将每一行分解成二进制元素。例如,99 就是 64+32+2+1。然后把所有行上每个元素的数量加起来。最后,寻找一种能让对手所有行上所有二进制元素数量为偶数的玩法。
我们来看一个例子。假设轮到你了,场景如下。
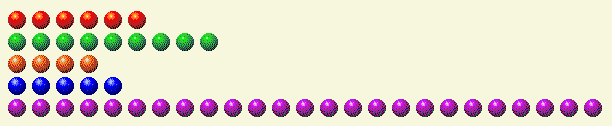
下表将每一行分解为二进制组件。
玩家第 1 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 二十五 | 1 | 0 | 0 | 1 | 1 |
| 全部的 | 3 | 1 | 3 | 2 | 1 |
可以看到,1、2、4 和 16 的数量都是奇数。显然,我们需要让 25 这一行小于 16,才能消除 16 这个数字。为了使二进制数字的和保持偶数,我们需要去掉 1,加上 2,加上 4,保留 8,然后去掉 16。这意味着最佳玩法是最后一行 2+4+8=14。保留最后一行 14,我们得到以下结果。
计算机的第一回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| 全部的 | 2 | 2 | 4 | 2 | 0 |
计算机轮流做事,把这个留给我们。
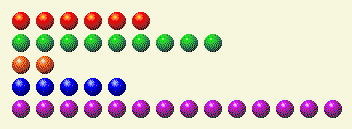
这是它的二进制分解。
玩家第 2 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| 全部的 | 2 | 3 | 3 | 2 | 0 |
这里我们需要去掉一个 2 和一个 4,才能使总数相等。只有一行,也就是 14,包含这两个部分。所以从中去掉 6,剩下 8。
计算机的第二回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| 全部的 | 2 | 2 | 2 | 2 | 0 |
计算机轮流做事,把这个留给我们。
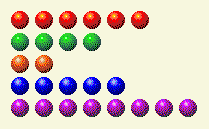
现在我们需要更改 1、4 和 8 列。
玩家第 3 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| 全部的 | 1 | 2 | 3 | 1 | 0 |
可以通过将行 8 更改为 5 来实现,如下所示。
计算机第 3 轮
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 全部的 | 2 | 2 | 4 | 0 | 0 |
计算机轮流做事,把这个留给我们。
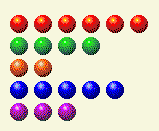
现在我们需要更改 2 和 4 的总数。
玩家回合 4
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 3 | 3 | 0 | 0 |
这可以通过将 6 更改为 0 来实现。
计算机第 4 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 2 | 2 | 0 | 0 |
计算机轮流做事,把这个留给我们。
现在我们需要改变 2 和 4。
玩家第 5 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 3 | 1 | 0 | 0 |
这可以通过将 5 行改为 3 行来实现。如果您能让对手陷入 x,x,y,y 局面,您就必然会获胜,前提是您可以将同样的局面保持到最后。
计算机的第 5 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 4 | 0 | 0 | 0 |
接下来的几步,我让计算机继续按照 x,x,y,y 的模式走。这里计算机给我的结果是 2,2,3,2;所以我给它留下的是 2,2,2,2。

然后计算机给了我2,2,1,2。我留下2,2,1,1。
然后计算机给我的结果是2,2,1。我给它留下的是2,2。如果你能把对手的棋子分成两行,你就赢了,只要保持两行棋子相等就行了。

然后计算机给我留下一堆 2,然后我拿走 1。

游戏到此结束。
我知道当赔率达到或超过10倍时,看跌投注是个不错的选择。所以,比如说,如果点数是6或8,就下注5美元,外加50美元的免费赔率。我的问题是,为什么要等到点数?为什么不先在过线投注,然后如果点数是6或8,再用10倍的赔率投注呢?这样你既能获得赔率优势,还能在7/11的点数下注。我是不是漏掉了什么?
我同意。我不建议进行看跌或位置投注,因为正如你所说,赔率线投注比最高赔率投注更高。然而,有些人绝对必须直接投注点数。如果必须这样做,我建议在位置、买入和看跌之间做出最佳选择,我会在我的掷骰子部分更详细地解释这一点。
我和朋友在拉斯维加斯玩牌。我们大吵了一架,争论的是,在两副牌的游戏中,玩家总点数10,庄家点数7,双倍下注,还是玩家总点数11,庄家点数10,双倍下注,哪个从统计上看赔率更高。我以为是前者。
我的二十一点附录9就是为这类问题设计的。假设有6副牌,我的表格显示,8+2对7的加倍预期值为0.396342。8+3对10的加倍预期值为0.176919。所以你说得对,10对7的加倍是更好的选择。
你的网站太棒了,我从中学到了很多东西。德州扑克翻牌圈,你有20张牌可以让你赢。为什么你在河牌圈拿到牌的概率是67.5%,而不是86%(20/47 + 20/46)?我找遍了所有资料,但似乎还是想不通,尽管我知道这大概很简单。非常感谢你的帮助,谢谢!!
谢谢!你的方法是重复计算你需要的20张牌中的两张。你在转牌圈拿到你需要的20张牌中的一张的概率是20/47 = 0.4255。你在转牌圈没拿到一张,然后在河牌圈拿到一张的概率是(27/47)*(20/46) = 0.2498。所以总概率是0.4255 + 0.2498 = 0.6753。
我最近在当地部落赌场目睹了一起涉及掷骰子赌桌礼仪的情况,这让我很困惑,请您帮我解释一下。玩家“A”在开局掷骰时掷出一个数字,并确定了一个点数。下一轮掷骰时,“A”旁边的玩家(玩家“B”)拿起骰子掷出。不清楚他为什么这么做,甚至不知道他是否认识“A”。另一位玩家表示反对,指出“B”不是最初的掷骰者。经过荷官和赌桌管理员的一番讨论和思考,骰子被传给了下一位玩家(玩家“C”),他最终完成了这局(他最终掷出了7点)。
对于这种情况,这是否是正确的流程?如果是,其背后的逻辑是什么?如果玩家“A”出于某种原因不想再掷骰子,为什么不允许他放弃骰子?如果玩家“B”因为不懂游戏规则而拿起骰子,或者发牌员错误地将骰子放在他面前,那么骰子难道不应该回到“A”手中完成这局游戏吗?
我问了nextshooter.com的 Bone Man,他是这样回答的。
如果掷骰者以外的玩家拿起骰子并掷出,则应判为不叫牌、不掷骰,并将骰子交还给正确的掷骰者。虽然这确实是正确的裁决,但在某些情况下,如果结果对所有或大多数玩家有利,赌桌管理员可能会允许掷骰。在某些情况下,掷骰结果可能不会影响任何玩家的投注。此外……任何玩家都可以要求将骰子发送给下一位掷骰者以完成一手牌。在这种情况下,可以发送相同的骰子,也可以由新的掷骰者请求新的骰子。掷骰完成后,同一位掷骰者可以掷出自己的手牌,从而拥有多手牌。
掷20个骰子,得到大于100的点数的概率是多少?
我开始使用正态近似来解决这个问题,但超过100个点的概率太低,该方法不够准确。因此,我进行了825万次试验的随机模拟,其中101个点或以上的试验次数为127次。因此,概率约为65,000分之一。
又到了“一掷千金”的问题了。假设银行家和席琳·迪翁客串演出之后,你只剩下两个箱子,50万美元和100万美元。我猜银行家的出价会略低于75万美元。你会选哪个?如果剩下的两个箱子分别是0.01美元和100万美元呢?我想这完全取决于你是不是赌徒,和赔率没关系。我问这个问题的原因是,我想知道是否有人能赢得100万美元(即使他们选的是那个神奇的箱子)。
当奖金数额足以改变人生时,明智的玩家应该谨慎行事,而非最大化预期价值。一个好的策略应该是最大化预期幸福感。我认为衡量幸福感的一个好函数是你总财富的对数。假设一个人现有财富为 10 万美元,面临 0.01 美元和 100 万美元两种情况。选择“不交易”的预期幸福感为 0.5*log(100,000.01 美元) + 0.5*log(1100,000 美元) = 5.520696。设 b 表示玩家无所谓是否接受的银行报价。
对数(b)= 5.520696
b = 10 5.520696
b = 331,662.50 美元。
所以这位假设的玩家应该对银行出价 331,662.50 美元无动于衷。你投入的资金越少,就越应该谨慎行事。通常在游戏后期,银行出价接近预期价值,有时甚至会略高一些。玩家赢得百万美元的唯一合理情况是,他投入了大量资金,并且/或者银行出价异常低廉。制作人似乎喜欢勤劳的中产阶级,所以我们不太可能看到有人在涉及大额资金时如此傲慢。我也从未见过银行在游戏后期出价低于预期价值 90% 的金额。我们只有在某个无法停止赌博的堕落赌徒出现时才会看到有人赢得百万美元。当这种情况发生时,我会支持银行家。
喜欢你的网站!我刚刚看到你列出的拉斯维加斯二十一点赌桌及其优势的详细列表,所以我想问一下:假设有两张二十一点赌桌,一张优势为0.2%,最低投注额为10美元,另一张优势为0.4%,最低投注额为5美元。两张赌桌每手牌的亏损都是0.02美元。选择其中一张赌桌有什么优势吗?
谢谢。要回答这个问题,你首先得问问自己为什么要赌博。如果你想尽可能少输,那你根本就不应该玩。但是,如果你只是为了赌博的乐趣,我建议你选择10美元、0.2%利润率的游戏。预期损失是一样的,但更大的赌注能让你获得更多的满足感。
尼亚加拉赌场有一种牌九扑克边注,赔率不是固定赔率,而是累积奖金。我想知道累积奖金要达到多少才能让这个赌注收支平衡(假设你把牌局设定为最大化累积奖金的回报)。
盈亏平衡点是102,680.24美元。我刚刚在我的“牌九扑克边注”版块添加了对这个赌注的分析。
我不太懂扑克,但我确实觉得它很有趣,所以也许你可以为我澄清一些事情。最近我和妻子去拉斯维加斯旅行时,我们住在亚利桑那查理迪凯特酒店。我们住在这里的原因是因为他们在网站上宣传 2-4 美元的德州扑克游戏。第一天早上,我们走到扑克室,报名参加 2-4 美元的比赛。我注意到扑克小哥把我们的名字写在了 4-8 美元的栏目下面。于是我告诉他我们想要 2-4 美元的比赛(同一张纸上有一栏标有“2-4 美元”)。他说是 2-4 美元:翻牌前 2 美元,翻牌后 4 美元,转牌和河牌后 8 美元。我向他解释了 2-4 美元是什么意思:翻牌前和翻牌后都是 2 美元,转牌和河牌后都是 4 美元。他嘲笑我们,好像我们不知道自己在说什么,并说游戏不是这样玩的。我们剩下的旅程都在黄金海岸玩扑克。这种下注方式在扑克室正常吗?(我最后跟扑克室经理说,如果我们能玩得起4到8美元的德州扑克,我们就不会住在亚利桑那查理赌场了。)
我同意“2/4”游戏意味着转牌前下注2美元,转牌后下注4美元。然而,小盲注很可能是1美元。听起来,当亚利桑那查理赌场把一局游戏称为“2/4”时,他们指的是盲注,这意味着小盲注是2美元,大盲注是4美元,这意味着转牌后下注8美元。我以前从未听过这种用法,所以你感到惊讶也就不足为奇了。
附言:后来我从扑克室主管安东尼那里收到了以下内容。
我是一名扑克室管理员。我写信只是想告诉你德州扑克中扑克限额的正确表述。如果某个游戏被称为$2/4,它指的是下注。(只有在无限注的情况下,游戏才会以盲注来表示。)翻牌前和翻牌后是$2,转牌和河牌是$4。如果某个游戏被列为$2/$4/$8(我猜想上一位写信人实际上指的是这个,翻牌前是$2,翻牌后是$4,转牌和河牌是$8)。也可能某个游戏被列为$2/$4/$6/$8。只是传递一下信息,优秀的扑克室管理员希望人们获得尽可能多的信息。


