前 n 个整数之和的证明
本周我将证明一个比较简单的等式:1+2+3+…+n = n(n+1)/2。我会用两种非常直观的方式展示它。这是我目前为止最简单的证明。不过,在此之前,我先给大家带来我每周的例行逻辑谜题。
逻辑谜题
爱丽丝、鲍勃和科尔发表了以下声明:
- • 爱丽丝:鲍勃是个骗子。
- •鲍勃:科尔是个骗子。
- • 科尔:爱丽丝和鲍勃都是骗子。
这三个人要么总是说真话,要么总是说谎。他们都知道另外两个人是否说真话。那么,谁在说真话呢?
答案和解决方案请见简报末尾。
前 n 个整数之和的证明
每个人都应该知道,前n个整数之和是n(n+1)/2。换句话说,1+2+3+…+n = n(n+1)/2。我将给出两个简单的证明来解释为什么这是正确的。
方法一
很容易看出,数列的平均数是 (n+1)/2。数列的项数为 n。和等于项数与平均数的乘积 = n × (n+1)/2 = n(n+1)/2。
同样的方法也适用于求任意起始数和结束数的和。假设起始数为 a,结束数为 b,则平均值为 (a+b)/2,项数为 (a-b+1)。因此,数列中所有数字之和为 (a-b+1) × (a+b)/2。
方法二
下一个方法用图示更容易解释。请看下图,其中蓝色方块代表 1 到 5 的整数。
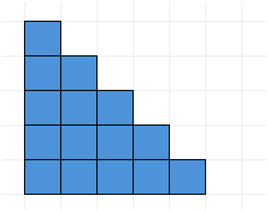
接下来,复制该部分,并将其放置在原件旁边,如下所示,形成一个矩形。
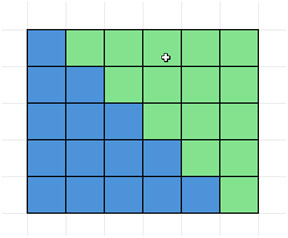
注意上图矩形的边长是 5 × 6。一般情况下,如果将 1 到 n 的整数相加,则矩形的边长是 n × (n+1)。然后,由于我们只要求其中一块区域的面积,所以需要将该面积除以 2。因此,这块区域的面积是 n(n+1)/2。
逻辑谜题解答
这三个人都有两种可能的状态:说真话或说谎。这样就有2³ = 8 种可能性。我把所有这些可能性都列在下表中。
| 设想 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 爱丽丝 | T | T | T | T | F | F | F | F |
| 鲍勃 | T | T | F | F | T | T | F | F |
| 油菜 | T | F | T | F | T | F | T | F |
注意,鲍勃和科尔互相指责对方说谎。这只有在他们之中一人说真话而另一人说谎的情况下才有可能。因此,我们可以排除鲍勃和科尔都说真话的四种情况。剩下的情况是第2、3、6和7种。让我们逐一分析。
在情景二中,已知爱丽丝说的是真话。她的真话意味着鲍勃是说谎者。然而,鲍勃在这个情景中也是说真话的,这就导致了矛盾。因此,情景二不成立。
在情景3中,已知爱丽丝是诚实的。她说鲍勃是骗子,这在情景3的假设下是正确的。然而,科尔也被列为诚实的人,但他却说爱丽丝在撒谎。爱丽丝不可能同时既诚实又撒谎,所以情景3不成立。
在情景7中,已知爱丽丝在说谎。她说鲍勃是个骗子,这没错。然而,这样一来,爱丽丝就成了说真话的人。爱丽丝不可能既说真话又说谎,所以情景7不成立。
这样就只剩下第六种情况了。我们来验证一下。如果爱丽丝说谎,那么鲍勃就是说真话的。如果鲍勃说真话,那么爱丽丝、鲍勃或者他们俩就都是说真话的。鲍勃说真话,所以科尔的说法是假的。因此,这个假设成立。鲍勃是唯一说真话的人。


