三角形内角和等于180度定理
众所周知,任意三角形的内角和为 180 度。在本期简报中,我将给出一个简单的证明。不过在此之前,我先奉上每周例行的逻辑谜题。
逻辑谜题
一位国王有49枚金币,每枚金币的重量分别为1克、2克、3克……49克。他如何将这些金币分给他的七个儿子,使得每个儿子都能得到7枚金币,且每枚金币的重量之和相等?
证明任意三角形的内角和为 180 度。
我先画一个任意三角形,并标注各个角。
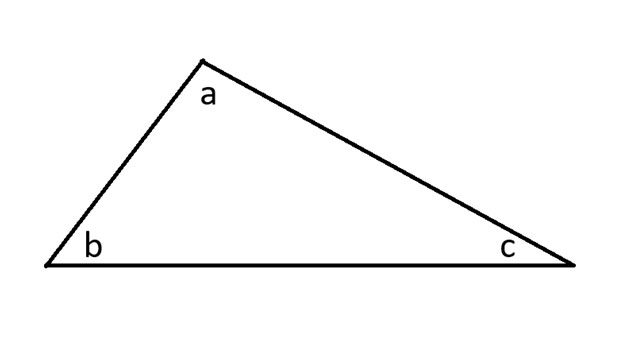
接下来,我将延长三角形的三条边,并画一条与角 a 相切的平行线。
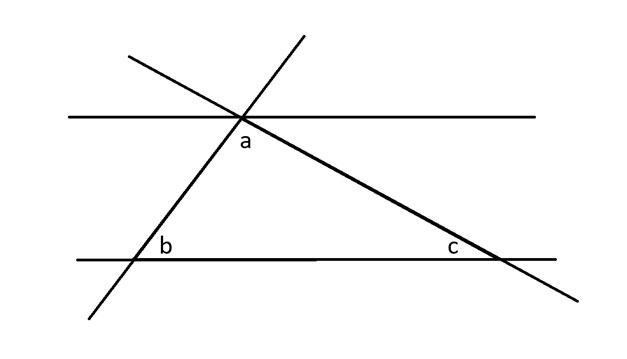
接下来,我将对角定理应用于角 b,该定理指出两条相交直线的对角相等。
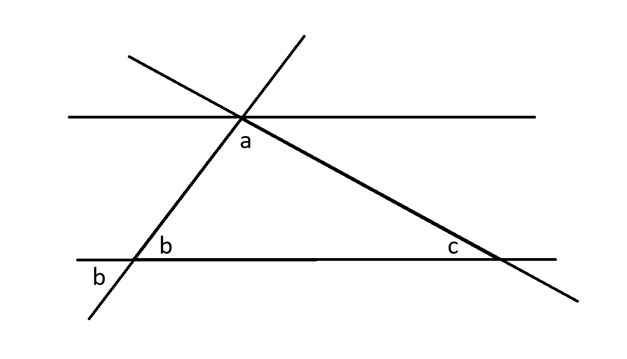
当一条对角线与一组平行线相交时,它与每条平行线相交处形成的角都相同。我利用这一点,在角 a 旁边画出另一个 b 度角。然后,我对角 c 也做同样的处理。
6; font-family: 'Open Sans', sans-serif; color: #313131 !important; ">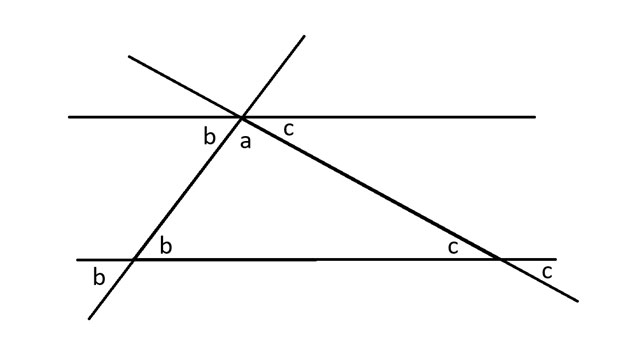
圆周角为360度,因此半圆周角为180度。换句话说,观察上方平行线下方的角,a + b + c = 180度。这三个角也是原三角形的内角和。因此,三角形内角和等于180度。
逻辑谜题解答
制作一个幻方,并将任意一列中的硬币分给每个儿子。你也可以按行分配硬币。“如何制作一个7x7的幻方呢?”你可能会问。以下方法被称为暹罗法,很久以前在印度就被发现了。
让我们从一个类似 7x7 战舰棋盘的网格开始。
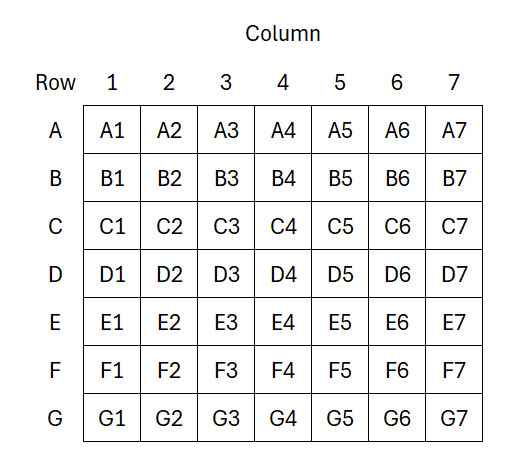
首先在A4单元格中输入1。然后按照以下规则操作:
- 下一个数字始终在前一个数字的基础上加 1。
- 始终朝西北方向走,除非该位置已被占用,或者你已经在 A 行或第 7 列。
- 如果您在 A 行,则转到 G 列获取下一个数字。
- 如果您在第 7 列,则下一个数字将循环到第 1 列。
- 呼叫 A7 将双向循环至 G1。
- 如果下一个要去的方格被占用了,那么就跳到下一个数字对应的方格(它应该是空的)。
我们是这样开始的:
- 1 在 A4 单元格中。
- 我们现在在 A 行,所以转到 G 行,在 G5 单元格中输入 2。
- 然后我们在 F6 中输入 3,在 E7 中输入 4。
- 我们现在在第 7 列,所以我们循环往复,在 D1 列输入 5。
- 在 C2 中填入 6,在 B3 中填入 7。
- 接下来我们要填入 A4,但是它被 1 占据了。所以,我们向下移动,把下一个数字 8 填入 C3。
- 重复此步骤直至魔方填满。
完工后的效果图如下:
这种方法适用于任何奇数维的幻方。
然后,决定是按行还是按列划分。每个儿子将某一行/列中的硬币分配给他们。例如,如果按列划分,那么第一个儿子将获得 30、38、46、5、13、21 和 22 枚硬币。


