勾股定理的证明
本周,我将证明经典的勾股定理,即直角三角形两直角边平方和等于斜边平方。最著名的例子是边长分别为 3、4 和 5 的直角三角形。注意3² + 4² = 5² 。不过,在此之前,我先给大家带来每周例行的逻辑谜题。
逻辑谜题
一位心不在焉的古代哲学家忘记给挂在屋子墙上的大钟上弦。他没有收音机、电视、电话、互联网,也没有任何其他计时工具。于是,他沿着笔直的沙漠公路步行几英里,去拜访朋友。他在朋友家住了一晚,回来时,他已经知道如何调好钟了。他是怎么知道的呢?
答案在简报末尾。
勾股定理的证明
请看下图,它由一个被分成四个全等直角三角形的大正方形和一个位于中间的小正方形组成。中间之所以会有一个小正方形,是因为任意三角形的内角和为 180 度。我在2025 年 11 月 13 日的简报中证明了这一点。
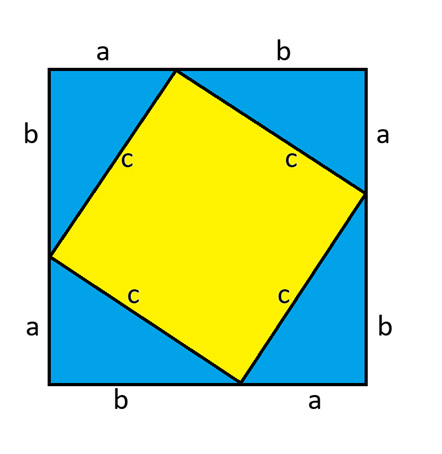
大正方形的面积为 (a+b) ² 。每个三角形的面积为ab² 。中间黄色正方形的面积为c² 。将大正方形的面积等于其内部各部分面积之和,我们得到:
6; font-family: 'Open Sans', sans-serif; color: #313131 !important;">(a+b) 2 = 4 ab 2 + c 2
a² + 2ab + b² = 2ab + c²
两边同时减去 2ab,得到:
a² + b² = c²
逻辑谜题解答
- 教授给钟上了发条,然后随意设定了一个时间。
- 当他到达朋友家时,他记下了到达时间。
- 离开时,他会记下离开的时间,并通过从离开的时间中减去到达的时间来计算在朋友家停留的时间。
- 他小心翼翼地以去朋友家时的速度返回。
- 当他回到家时,他的时钟会显示他在朋友家的时间加上步行时间。他可以通过从总时间中减去在朋友家的时间来计算步行时间。然后,他可以通过将总步行时间除以 2 来计算单程时间。
- 然后他可以将时钟设定为离开朋友家的时间加上单程步行时间。
我们来看一个例子。
他把错误的钟表上紧了发条,并调到了12点。实际时间是8点,他到达朋友家。1点钟他离开,记下这次拜访花了5个小时。回来时,他发现自己的钟表显示8点。减去5个小时的拜访时间,意味着他总共走了3个小时。也就是说,单程花了1.5个小时。如果他1点钟出发,走了1.5个小时,那么现在应该是2点30分,于是他把钟表调到了2点30分。


