贱女孩数学问题
你可能还记得,在上周的新闻通讯中,我介绍了电影《心灵捕手》中的第二个数学难题。你可能还记得,这部电影声称麻省理工学院数学系花了两年时间才解决。正如我上周所展示的,这道题不仅相当简单,而且马特·达蒙饰演的数学天才角色也只给出了 80% 的答案。
本周我们将关注另一部以数学问题为重要情节点的电影。这部电影就是《贱女孩》。在一场高中数学竞赛中,林赛·罗韩饰演的凯蒂需要回答以下问题:
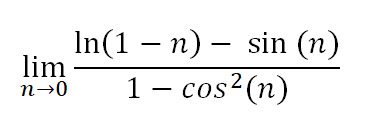
您可以在以下 YouTube 视频中看到相关场景。问题出现在 4:53 处。

如果我们可以使用电子表格,我们可以很容易地看到,当 x 从负数趋近于 0 时,f(x) 趋近于无穷大。当 x 从正数趋近于 0 时,f(x) 趋近于负无穷大。因此,我们可以借助计算机看到,由于该函数同时趋近于负无穷大和正无穷大,因此它不会趋近于任何特定的值。因此,极限不存在。
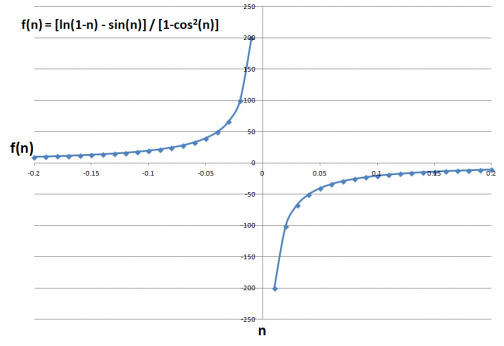
然而,电影里不允许他们使用电脑。为了解决这个问题,让我提醒你洛必达法则
它的基本意思是,如果 f(x)/g(x) 的极限 = 0/0,则 lim f(x)/g(x) = lim f'(x)/g'(x)。其他一些条件,我就不一一列举了,请参阅上面的链接。
请不要写信告诉我,我忘了在 L'Hospital 的 o 上方加一个抑扬符。我觉得两种拼写都可以。我仍然不确定这个发音该怎么读,很高兴为了这篇简报不用再纠结了。
让我首先发布另一个适合使用洛必达规则的问题。它取自我之前链接到的维基百科页面。
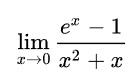
当 x 的极限趋近于 0 时,分子和分母都会趋近于 0。我们无法对 0/0 做任何处理。根据洛必达法则,我们可以对分子和分母分别求导,然后取该分数在 x 趋近于零时的极限。我们来试试吧。
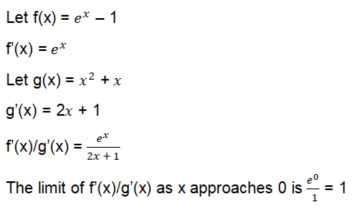
我们走了,洛必达来救援了。
现在,让我们回到《贱女孩》的极限。
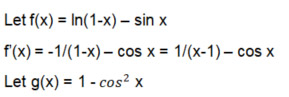
让我们使用乘积规则来区分 g(x):回想一下,它说 (r(x) * s(x))' = r(x)*s'(x) + r'(x)*s(x)。
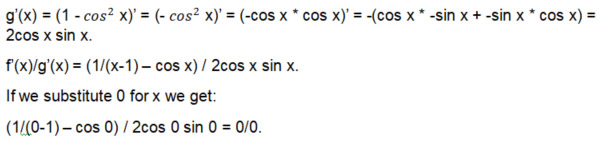
所以,洛必达对解决“贱女孩”的问题毫无帮助。因为我们仍然保留着毫无意义的0/0,所以我们可以放心地说“没有限制”。在这场戏里,凯蒂是对的,她的团队当之无愧地赢得了比赛。
我要把所有应得的赞誉都归功于这部电影的主编蒂娜·菲,她把数学计算得非常准确!这可不是想当然的事情。就像我们在《心灵捕手》中看到的那样,即使是最精良的高预算电影,也会犯一些数学和科学错误,让我毛骨悚然。


