2025年疯狂三月
逻辑谜题
在进入本周疯狂三月的统计数据主题之前,我们先来做一下每周例行的逻辑谜题。就在这里。
三位玩家进行游戏。在玩家看不见的情况下,掷出三枚硬币,每位玩家一枚。根据掷出的硬币,该玩家会被蒙上眼睛,并被给予一顶黑色或白色的帽子。之后,摘下眼罩,每位玩家可以看到其他两位玩家的帽子,但看不到自己的帽子。
然后,每位玩家都会得到一张无记名投票,记录自己帽子的颜色。选项包括黑色、白色和“通过”。实验成功的关键在于,所有投白色或黑色的玩家都必须正确。然而,如果三位玩家都投了“通过”,则实验失败。
玩家需要一些时间来制定策略。他们可以采用什么策略才能获得 75% 的成功率?
疯狂三月更新
我以前经常在疯狂三月的投注中投入巨资。一个典型的例子就是预测太平洋十二校联盟球队总胜场数的盘口。为了进行这样的让分投注,了解特定种子球队的预期胜场数是很有帮助的。
有些投注在第一轮就已结算。例如,13号种子或以上的球队能否赢得比赛?以下是今年封面上的一些例子。
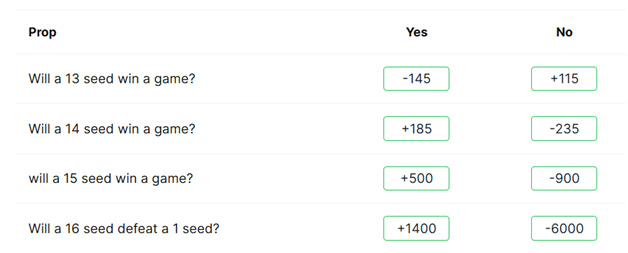
下表显示了特定种子队以及该种子队四支球队中任意一支在第一轮比赛中获胜的概率。该表格基于 1985 年至 2025 年 NCAA 锦标赛的 40 年历史。
| 种子 | 特定队伍获胜 | 任何球队赢得第一轮 |
|---|---|---|
| 1 | 98.75% | 100.00% |
| 2 | 92.50% | 100.00% |
| 3 | 85.63% | 99.96% |
| 4 | 79.38% | 99.82% |
| 5 | 64.38% | 98.39% |
| 6 | 61.25% | 97.75% |
| 7 | 61.25% | 97.75% |
| 8 | 50.00% | 93.75% |
| 9 | 50.00% | 93.75% |
| 10 | 38.75% | 85.93% |
| 11 | 38.75% | 85.93% |
| 12 | 35.63% | 82.83% |
| 十三 | 20.63% | 60.31% |
| 14 | 14.38% | 46.25% |
| 15 | 7.50% | 26.79% |
| 16 | 1.25% | 4.91% |
今年,首轮晋级的平均种子排名为5.34。总锦标赛平均排名为5.84。
第二轮,晋级甜蜜十六强的平均种子排名为3.44。锦标赛平均排名为4.52。晋级两轮的最低种子排名是10。换句话说,今年的弱队在前两轮表现不佳。
第三轮,晋级八强的平均种子排名为1.625。锦标赛平均排名为3.30。晋级三轮比赛的最低排名种子排名为3,其中仅有1场。这追平了锦标赛最低排名种子排名3的纪录。这种情况之前曾发生过两次,分别在2007年和2009年。1.625的平均种子排名创下了锦标赛历史上的新低。
在最终四强赛中,四支球队全部都是排名第一。这种情况在锦标赛历史上只发生过一次,那是在2008年。现在有一个很受欢迎的投注,赌究竟有多少支一号种子球队能进入最终四强。以下是今年Covers的投注。
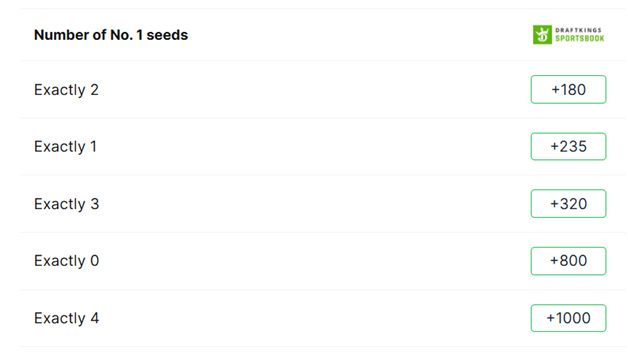
下表显示了 40 年的锦标赛历史中有多少头号种子球队进入了四强。
| #1 种子 | 数数 | 可能性 |
|---|---|---|
| 4 | 2 | 5.00% |
| 3 | 4 | 10.00% |
| 2 | 15 | 37.50% |
| 1 | 16 | 40.00% |
| 0 | 3 | 7.50% |
| 全部的 | 40 | 100.00% |
任何特定的一号种子进入四强的概率为 41.25%。
毋庸置疑,由于四强赛中的所有四支球队都是一号种子,因此两支一号种子球队将进入冠军赛并赢得冠军。
另一个投注选项是冠军争夺战的种子队。以下是今年的“封面”投注。
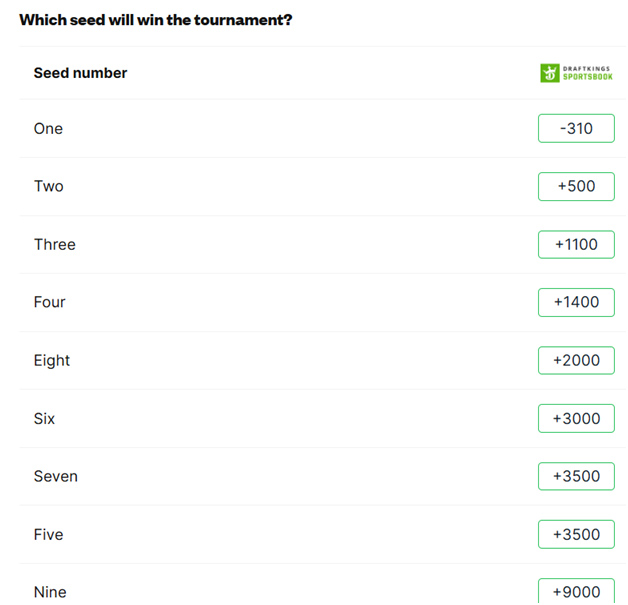
下表显示了每个种子队赢得冠军赛的次数。
| 获胜种子 | 数数 | 可能性 |
|---|---|---|
| 1 | 二十六 | 65.00% |
| 2 | 5 | 12.50% |
| 3 | 4 | 10.00% |
| 4 | 2 | 5.00% |
| 5 | 0 | 0.00% |
| 6 | 1 | 2.50% |
| 7 | 1 | 2.50% |
| 8 | 1 | 2.50% |
| 9至16岁 | 0 | 0.00% |
| 全部的 | 40 | 100.00% |
回到种子预期胜利,这里有一个更新的表格,包括本赛季的数据。
| 种子 | 平均胜场数 |
|---|---|
| 1 | 3.34 |
| 2 | 2.33 |
| 3 | 1.84 |
| 4 | 1.56 |
| 5 | 1.14 |
| 6 | 1.06 |
| 7 | 0.89 |
| 8 | 0.73 |
| 9 | 0.59 |
| 10 | 0.61 |
| 11 | 0.64 |
| 12 | 0.51 |
| 十三 | 0.24 |
| 14 | 0.16 |
| 15 | 0.11 |
| 16 | 0.01 |
我经常被问到的一个问题是,完美分组的概率是多少。假设我的策略是每次都选择种子排名较高的比赛(或排名较低的比赛),除了在1对1的情况下随机选择外,我的更新概率(包括本赛季的数据)是287,548,153分之一。
逻辑谜题答案
该策略应如下:
- • 如果您看到两顶颜色相反的帽子,则通过。
- • 如果您看到两顶相同颜色的帽子,请选择相反的颜色。
根据这三种颜色,我们可以预期会发生以下情况:
- • 三黑:所有玩家看到两个黑色,并投白色。所有人都会猜错,因此实验失败。
- • 两黑一白:白方玩家将看到两顶黑色帽子,并正确投白票。两名黑方玩家将看到两种颜色各一顶,并投弃权票。实验成功。
- • 一黑两白:黑方玩家将看到两顶白帽子,并正确投黑。两名白方玩家将看到两种颜色的一顶白帽子,并投弃权票。实验成功。
- • 三白:所有玩家都会看到两白,并投黑票。所有人都会错,因此实验失败。
三个白色或三个黑色的概率是 2*(1/2) ³ = 25%。另一种选择是两种颜色按 2:1 的比例分配,概率为 75%。如上所示,如果按 2:1 的比例分配,实验将会成功。


