价格合适参赛者排
在进入正题之前,先更新一下。上周我写了关于火人节购票流程的文章。周三,我参加了主售票,碰碰运气。你们可能还记得,最后一个环节是准备好在3月30日中午12点准时购票。我准备好了。事实上,我准备了三个浏览器,里面都存着售票链接。说实话,我不确定这是否能提高我的中奖几率,但其他关于火人节的信息来源建议我这样做。
长话短说,我没买到票。这在意料之中。至少我尝试过了。与2019年不同,你在我的屏幕上看到的图片是在售票开始后大约半小时更新的,显示门票已售罄。你可能想知道我是不是点击了“返回”,屏幕上显示这没用。我没有。
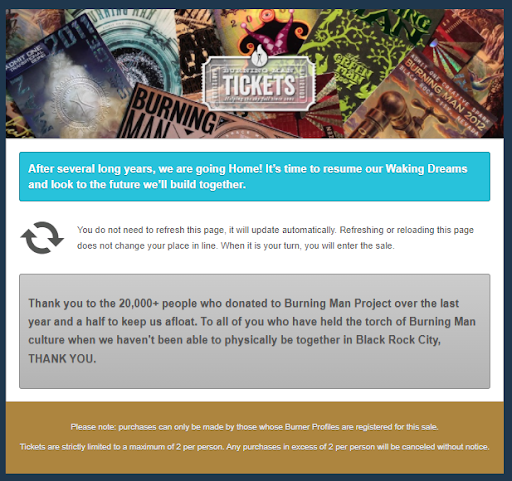
所以,看来我今年去不了火人节了。没关系。我还有很多其他的度假计划。
回到正题,《价格猜猜猜》节目中的参赛者争吵。这个游戏每期节目都会进行六次。对于那些还不知道规则的人来说,规则如下:
- 选择四名玩家参加下一场定价游戏。
- 展示的物品通常价值在 1,000 美元到 2,000 美元之间。例如,一辆漂亮的自行车。
- 玩家将按照指定的顺序对物品的价值进行出价。
- 出价最接近实际价值且不超过的玩家将赢得该物品并进入下一个定价游戏。
- 如果四位玩家都出价过高,则按相同顺序重新出价,并被告知出价不得超过上一轮的最低出价。此操作将持续进行,直到至少有一位玩家出价过高为止。

假设您对奖品的价值一无所知,那么您在这场游戏中的策略应该是什么?
节目里大多数参赛者的策略都很差。假设你是最后一个出价的,之前的出价分别是1500美元、1600美元和2400美元。同样,你对物品的价值一无所知,最佳出价应该是:
- $1:涵盖 1499 美元的范围- 价值从 1 美元到 1499 美元,但奖金从未接近 1 美元。
- $1601:涵盖 800 美元的范围- 价值从 1,600 美元到 2,399 美元。
- $2401:这涵盖了无限范围——从 $2,400 到无穷大的值。
你经常会看到玩家出价时不必要地放弃范围。比如上例中,2000 美元的出价,就等于放弃了 1600 美元到 1999 美元的范围,而 1600 美元的出价则毫无意义。
没有哪条经验法则能涵盖所有情况。只需尽量覆盖尽可能广泛的范围,尤其是在奖金容易下跌的范围内。
你可能会问,如果是四位逻辑学家一起玩会怎么样?我们假设这些逻辑学家对奖品的价值一无所知。为了便于解释,我们假设参赛者可能会竞标到一分钱。
6;font-family: 'Open Sans',sans-serif;color: #313131!important">让我们从一个简单的情况开始,奖金的金额是随机的,并从0美元到1000美元的均匀分布中选出。最后一个出价显然有位置优势。我不会深入讨论数学,但以下是四位逻辑学家应该如何出价,按照从第一个到最后一个的顺序:- 玩家 1: 777.80 美元
- 玩家2: 555.57美元
- 玩家3: 333.33美元
- 玩家 4: 0.01 美元、333.34 美元、555.57 美元或 777.79 美元。
关键在于,前三名玩家希望所有后续玩家都处于几乎无差异的境地。他们每个人都想尽可能地减少空间,同时又不鼓励后续玩家出价比他们高出0.01美元。
如果他们这样出价,无论我列出的四种可能的出价是什么,玩家4的获胜概率都是33.3%。其他玩家的获胜概率均为22.2%。我在玩家1和2的出价基础上加了一到两美分,以确保玩家3和4的出价不会超过他们0.01美元。
然而,这是一个不切实际的例子,因为奖金的价值往往更符合指数分布。为了更贴近现实,假设奖金的价值是从平均值为 1,000 美元的指数分布中随机选择的。
无需进行数学计算,以下是上述假设下的最佳出价:
- 玩家1: 1,504.08美元
- 玩家2: 810.98美元
- 玩家3: 405.47美元
- 玩家 4: $0.01、$405.48、$810.99 或 $1,504.09
获胜的概率与第一种情况相同,玩家 4 的获胜概率为 33.3%,其他所有人的获胜概率为 22.22%。
本周就到这里。下次再见,祝你好运。


