圆周角定理证明(第二部分)
你可能还记得,上周我开始证明圆周角定理。这周,我们将完成它。不过,在此之前,我先给大家带来我每周的例行逻辑谜题。
逻辑谜题
下列哪些说法是正确的?
- 这些说法中有一条是错误的。
- 这两项陈述中有两项是错误的。
- 这三项陈述是错误的。
- 这四项陈述中有四项是错误的。
- 这五项陈述是错误的。
- 这六项陈述是错误的。
- 这七项陈述都是错误的。
- 这八项陈述是错误的。
- 这九条陈述都是错误的。
- 这十条陈述是错误的。
答案在简报底部。
圆周角定理(第二部分)
让我来提醒你一下圆周角定理的内容。
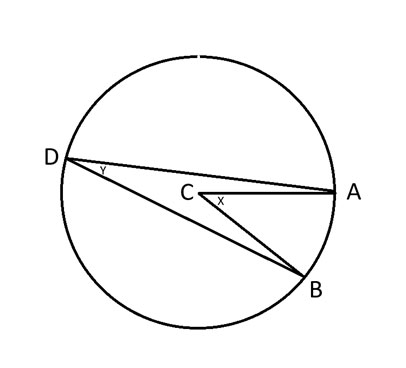
A、B、D = 圆上的任意三个点。
C = 圆心。
x = 角 ACB。
y = 角度 ADB。
圆周角定理指出,角 2y = x。
上周我证明了当 AD 或 BD 构成圆的直径时,这个结论成立。本周我将以此为例,证明该定理对于 D 的一般情况也成立。
我将按如下方式列出D的所有可能位置:
情况 1 = AD 或 BD 构成圆的直径(上周已证明)
情况 2 = D 位于(或者说“位于”?)圆弧上,与 A 和 B 相对。
情况 3 = 所有其他情况
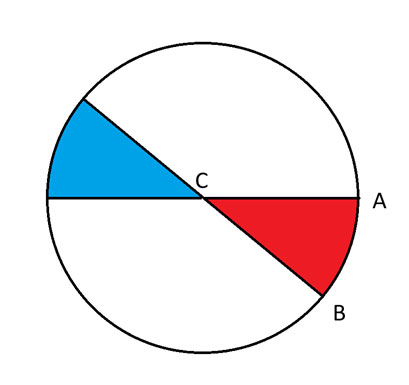
换句话说,情况 2 将涵盖 D 位于蓝色区域内圆周边缘的情况。情况 3 将涵盖 D 位于蓝色区域之外的其他位置的情况。
让我们用下图进行讨论。
让:
x = x1 + x2
y = y1 + y2
z = z1 + z2
我们努力证明 x = 2y
我仔细地从D点到C点画了一条线,这条线构成了圆的直径。E点是它与圆的另一侧相交的点。
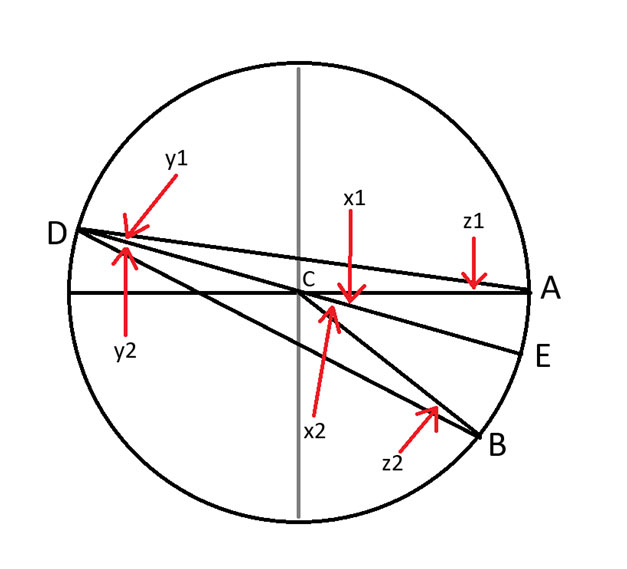
角度中的数字应该加下标,但是我的绘图软件不允许。
考虑三角形 ADE。
由于 DE 构成直径,我们可以利用上周证明的结论来证明 2x1 = 2y1。
现在考虑三角形EDB。
按照同样的逻辑, 2x² = y² 。
将以下方程式相加:
2x₁ + 2x₂ = y₁ + y₂
2( x₁ + x₂ ) = y₁ + y₂
2x = y
案例二就讲完了。
我们来看案例 3。

在这里,我们努力证明 2x 1 = y 1 。
案例1:
2x² = y²
2(x 1 + x 2 ) = y< 1 +y 2
将下面的等式减去上面的等式:
2x 1 = y 1
我们已经证明了第三种情况。
逻辑谜题答案
只有第9条是正确的。
逻辑谜题解答
我们有十个相互矛盾的说法。如果十个人各执一词,要么只有一个人是对的,要么所有人都是错的。
我们考虑十个陈述全部为假的情况。这样一来,第十个陈述就为真。这意味着只有九个陈述为假。因此,这构成矛盾。必然存在一个为真的陈述。但究竟是哪一个呢?
如果其中一条陈述为真,那么其余九条陈述均为假。正是第九条陈述表明了这一点。因此,只有第九条陈述为真。


