圆周角定理证明(第一部分)
本周我们继续我的数学定理证明主题。本周的定理是圆周角定理。这个证明比以往的要复杂一些,所以我将把它分成两部分,第二部分下周发布。不过,在此之前,我先给大家带来我每周的例行逻辑谜题。
逻辑谜题
在下图所示的示意图中,移动一枚硬币,使之形成两排各四枚硬币的直线。
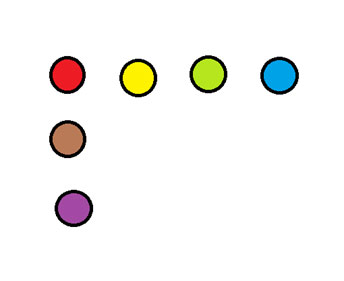
答案在简报底部。
圆周角定理证明(第一部分)
在解释圆周角定理之前,让我先定义下图所示的圆上的一些点。
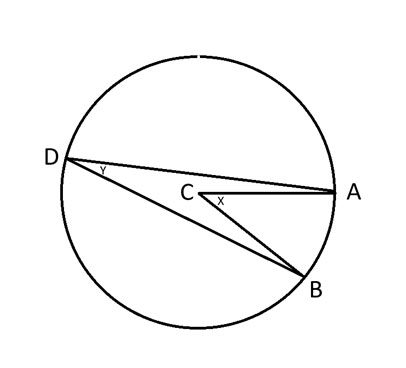
A、B、D = 圆上的任意三个点。
C = 圆心。
x = 角 ACB。
y = 角度 ADB。
圆周角定理指出,角 2y = x。
在本期简报中,我将尝试证明 AD 或 BD 构成圆的直径这一特定情况。下周,我将扩展讨论 D 位置的一般情况。
我们将 AD 构成圆的直径这一特殊情况称为情况 1。下面是这种情况的新图。
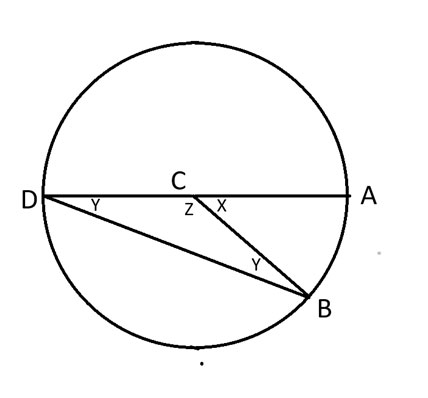
在上图中,AD 构成以 C 为圆心的圆的直径。
我们可以说 x+z = 180 度,因为它们构成了圆周 360 度的一半。
∠BCD 构成等腰三角形。因此,∠CDB = ∠CBD = y。
正如我在2025年11月13日的简报中所证明的,三角形内角和等于180度。换句话说,z + 2y = 180度。
让我们重写这两个方程:
z = 180 – x
z = 180 – 2y
让我们把它们都写成方程,因为它们都等于 z。
180 – x = 180 – 2y
-x = -2y
x = 2y。
我们已经证明了圆周角定理的一个特例,即圆上两点构成直径的情况。下周我们将以此为基础,证明圆周角定理的一般情况。
逻辑谜题解答
将蓝色硬币移到红色硬币上方。下图中的数字表示每堆硬币的数量。
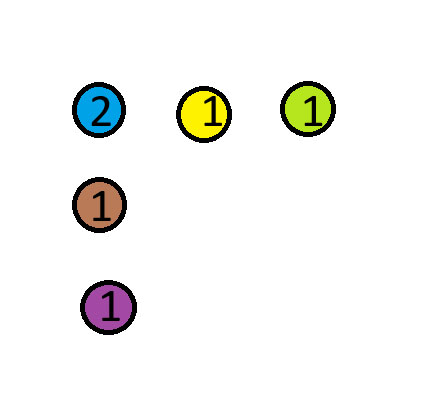
致谢:我从“Mind Your Decisions” YouTube频道获得了这个谜题。这是链接视频中的第三个谜题。


