欧拉恒等式
本周我们来挑战一个大难题:证明欧拉恒等式。如果你忘了,它或许是数学中最美的恒等式:e ^(πi +1) = 0。我太喜欢这个恒等式了,它印在我的名片上,我甚至可能把它纹在身上。不过,在此之前,我先奉上每周例行的逻辑谜题。
逻辑谜题
你有四条链子,每条链子由三个链环组成。如何将它们连接起来,形成一个包含12个链环的圆环,并且只能剪掉其中三个链环?
证明欧拉恒等式
数学中最著名的方程式之一是欧拉恒等式,它表示 e πi +1 = 0。它的神奇之处在于它结合了数学中最重要的五个数字:0、1、e、π 和 i。
我的解法需要用到泰勒展开式的公式。提醒一下,公式是:
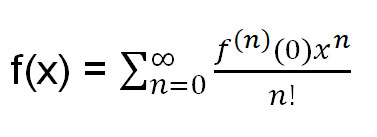
其中 f (n) (0) = f(x) 在 0 处的 n 阶导数。
我个人认为这个方程式是数学中最令人惊叹、最美丽的方程式之一。对我而言,它证明了数学中蕴含着某种神圣的特质。
也就是说,以下是我们将要用到的三个常用函数的泰勒展开式:
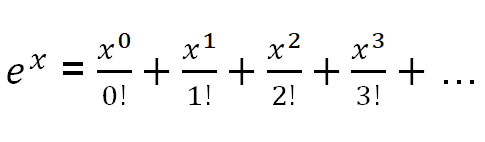
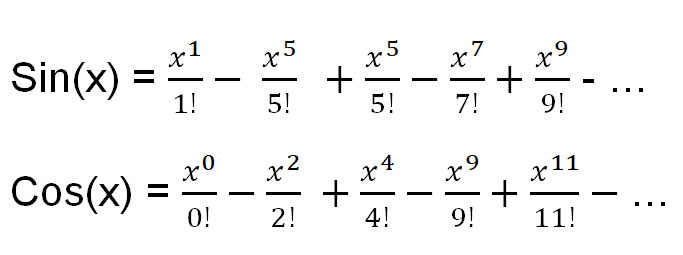
让我们利用 e x的泰勒展开式来求 e πi 。
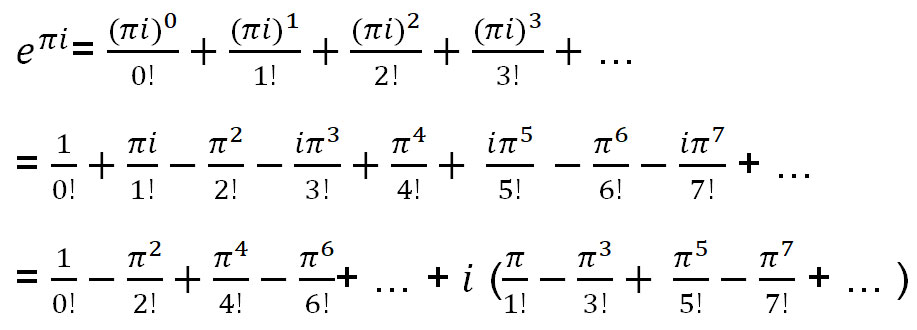
上述方程可以表示为 sin(x) 和 cos(x) 的函数:
= cos(π)+i ×sin(π)
= -1 + i ×0
= -1
所以,我们有 e πi = -1。这可以重新整理成通常的形式:
e πi +1 = 0
逻辑谜题解答
- 取四条链中的一条,将其打开并分开所有三个链环。将另外三条链分别称为 1、2 和 3。
- 使用一个连接环将链 1 和链 2 连接起来,形成一个七环链。
- 使用另一个链环将步骤 2 中的七链与链 3 连接起来,形成一个 11 链。
- 使用最后一个链环将步骤 3 中的 11 链环的两端连接起来,形成一个 12 链环的圆圈。


