折叠矩形拼图
在本期通讯中,我展示了门萨公报 11 月刊中的一道数学谜题。
假设有一个 1x4 的矩形。现在,将它折叠起来,使对角重叠,如下图所示。
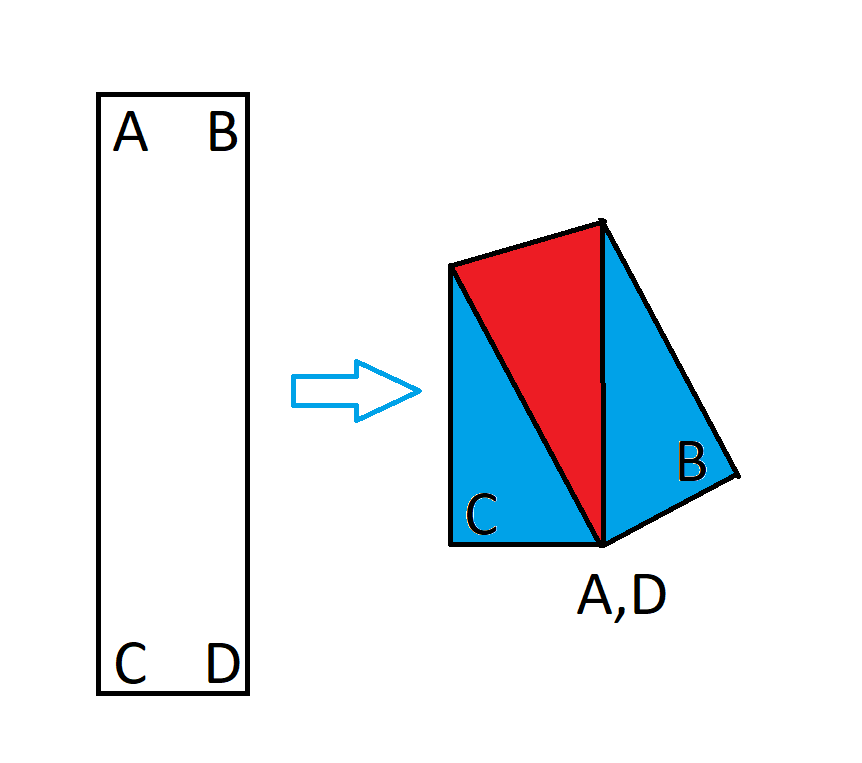
矩形折叠后,形成一个不规则的五边形。五边形与纸张重叠的部分与总面积的比值是多少?换句话说,就是上图中红色区域与总面积的比值。
向下滚动查看答案和解决方案。
回答
答案是 17/47 = 约 0.3617
解决方案
为了解释这个解,我先定义几个点,如下图所示。F 是 E 和 G 的中点。
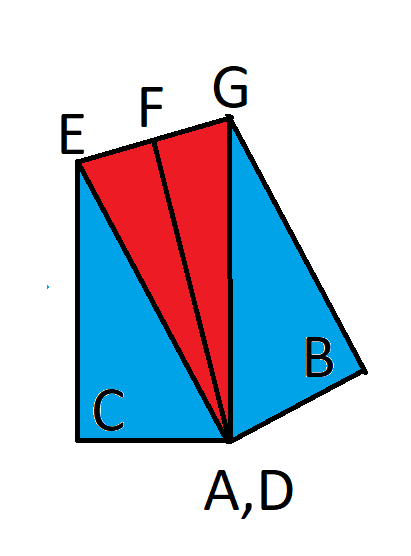
我们知道:
交流电=1
CE + AE = 4
让我们使用勾股定理来求解 AE:
1 2 + (CE) 2 = (AE) 2
用 4 – CE 代替 AE 可得:
1 2 + (CE) 2 = (4 – CE) 2
1 + (CE) 2 = 16 – 8(CE) + (CE) 2
8(CE) = 15
CE = 15/8
回到 1 2 + (CE) 2 = (AE) 2 ,由于我们知道 EC,我们可以解出 (AE):
(AE) 2 = (CE) 2 + 1 2
(AE) 2 = (15/8) 2 + 1 2
(AE) 2 = 225/64 + 64/64
(AE) 2 = 289/64
6;字体系列:'Open Sans',sans-serif;颜色:#313131!重要">AE = 17/8折叠前,A 到 D 的长度是矩形的对角线。再次使用勾股定理,长度为 sqrt(17)。
(AF) 是该长度的一半,或 sqrt(17)/2。
知道了 AE 和 AF,我们可以再次使用勾股定理来求解 EF:
(AE) 2 = (EF) 2 + (AF) 2
(17/8) 2 = (EF) 2 + (sqrt(17)/2) 2
289/64 = (EF) 2 + 17/4
289/64 = (EF) 2 + 272/64
(EF) 2 = 17/64
EF = sqrt(17)/8
如前所述,F 是 E 和 G 的中点。因此 EG = 2*sqrt(17)/8 = sqrt(17)/4。
红色三角形,AEG = (1/2) × 底 × 高 =
= (1/2) × sqrt(17/4) × sqrt(17)/2
= (1/2) × (17/8) = 17/16
三角形 ACE 的面积 = (1/2)*底*高 =
(1/2)×1×(15/8)=15/16。
整个五边形的面积 = AEG + 2*ACE =
(17/16)+ 2*(15/16)= 47/16
因此,红色区域占整个五边形的面积=
(17/16)/(47/16)= 17/47 = 约 0.3617


