爱丽丝琐事
本周,我们向波莉·霍利迪致敬,她于9月9日去世,享年88岁。她最出名的角色是电视剧《爱丽丝漫游奇境记》中那个泼辣的女服务员弗洛。令人遗憾的是,波莉是该剧最后一位离世的主要演员。没错,就连饰演汤米的菲利普·麦基翁也于2019年去世,享年55岁。
这部电视剧从1976年播到1978年,当时我大概11到13岁。它是我最喜欢的电视剧之一,我经常重播。几年前,我去凤凰城的时候,去了一趟真正的梅尔餐厅(Mel's Diner),这部电视剧就是以它为原型的。可惜我去的时候已经很晚了,餐厅关门了。
为了纪念波莉·霍利迪,我准备了一场爱丽丝问答挑战,题目都是我亲自挑选的。不过,在此之前,我先来介绍一下我们每周的逻辑谜题,以及wizardofodds.com在《危险边缘》节目中的表现!
《危险边缘》
2025 年 9 月 11 日播出的《危险边缘》节目给出了以下线索。
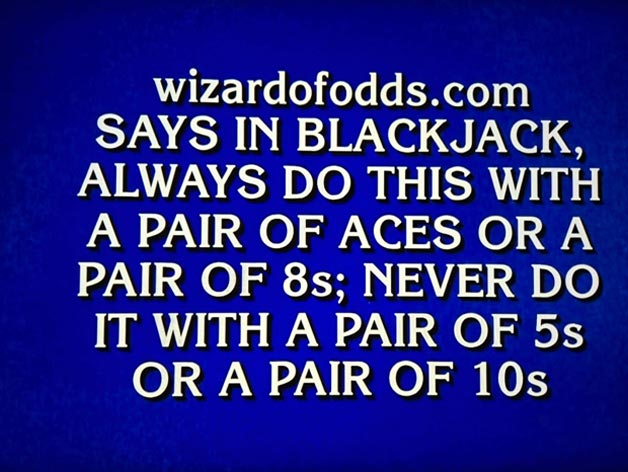
答案当然是“分裂”。作为《危险边缘》的忠实粉丝,我很自豪自己创办的网站被提及。真正上节目一直是我的梦想,可惜的是,我只能在线索里被提及了。
逻辑谜题
找出一个10位的“自传数”。这个数用从0开始的每个位置上的数字来描述自己,等于该数字在整数中的计数。
例如,1210 是 1,因为:
0 位置上有一个 1,整个数字中有 1 个数字 0。
1 位置上有一个 2,整个数字中有 2 个数字 1。
2 位置上有一个 1,整个数字中有 1 个数字 2。
3 位置上有 0,整个数字中有 0 个数字 3。
爱丽丝琐事问题

- 请说出最初的三位女服务员的名字。
- 节目中出现的餐馆叫什么名字?
- 唯一一位在电影和电视剧中扮演同一角色的演员是谁?
- 说出爱丽丝儿子的名字。
- 说出《爱丽丝》唯一的衍生作品。
- 演出在哪个城市举行?
- 爱丽丝真正想从事什么职业?
- 弗洛离开后谁来接替她?
- 当她离开时,谁取代了第 6 题的答案?
- 弗洛的口头禅是什么?
- 《爱丽丝》与哪部其他热门节目并列 1977 年、1980 年和 1983 年最受欢迎节目?
- 正如电影和电视节目所解释的那样,是什么让爱丽丝找到了问题 5 的答案?
- 爱丽丝从哪里搬来的?
- 顾客们究竟喜欢餐馆里的什么食物?
- 梅尔给维拉起了什么昵称?
- 该节目的主题曲是什么?
- 亨利的职业是什么?
- 这部电视剧的灵感来自哪部电影?
- 爱丽丝居住的公寓大楼叫什么名字?
- 维拉在后几季中的男朋友是谁?
- 爱丽丝的儿子(来自问题 3)玩什么运动?
- 梅尔分分合合的女友是谁?
- 梅尔的竞争对手餐厅叫什么名字?
- 梅尔对什么上瘾了?
- 汤米由演员菲利普·麦基翁饰演。他的妹妹是南希·麦基翁,她因在另一部电视剧中扮演的什么角色而闻名?

爱丽丝问答
- 爱丽丝·海厄特、弗·路易丝·戈尔曼、弗洛·卡斯尔贝里
- 梅尔的餐厅
- 维克·泰贝克饰演梅尔。其他一些演员也参演了两部影片,但饰演的角色不同。
- 汤米·海亚特
- 弗洛
- 凤凰
- 歌手
- 美女
- 乔琳·亨尼卡特
- “亲吻我的粗燕麦粉!”
- 捣碎
- 爱丽丝的车在去洛杉矶的路上抛锚了。
- 新泽西州
- 梅尔的辣椒
- 昏暗的
- 镇上来了一位新女孩
- 电话公司修理工
- 爱丽丝不再住在这里
- 沙漠太阳
- 艾略特
- 篮球
- 玛丽·梅西
- 维尼小牛肉屋
- 赌博
- 她在《生活的真相》中扮演乔的角色。
大多数问题的来源: Howstuffworks
逻辑谜题答案
6210001000
逻辑谜题解答
首先考虑第一个数字,从 9 开始。
如果第一位是 9,就意味着有 9 个零。只剩下 9 个位置,所以必须是 9000000000。但是,9 的最后一个位置至少需要是 1。所以,第一位不能是 9。
如果第一位是 8,那就意味着有 8 个零。我们需要倒数第二个数字至少有一个 1 来代表这个 8。这样就得到了 8000000010。然而,第九位上的 1 需要第二个数字也有一个 1。所以,第一个数字 8 是不行的。
如果第一位是 7,则意味着有 7 个零。我们需要在倒数第三位至少有一个 1 来匹配这个 7。这样就得到了 7000000100。我们需要在第二位至少有一个 1 来匹配第八位上的 1。这样就得到了 7100000100,它有两个 1。让我们将第二位增加到 2:7200000100。现在我们需要在第三位添加一个 1 来匹配第二位上的 2。但是,我们没有更多的 0 可以去掉了,因为我们需要 7 个 0。在第三位添加 1 也会导致 1 出现问题。因此,第一位不能是 7。
如果第一位是 6,就意味着有 6 个零。我们需要在第 7 位至少有一个 1 来表示这个 6。这样就得到了 6000001000。我们需要在第 2 位至少有一个 1 来表示第 7 位上的 1。这样就得到了 6100001000。现在有两个 1,所以我们需要将第 2 位增加到 2,并找到另一个 1 放在某个位置。目前,我们得到的是 6200001000。我们可以在第三位放置一个 1,这样既能得到额外的 1,又能识别第 2 位上的 2。这样我们就得到了 6210001000。成功了!
我可以继续证明没有其他解决方案,但我会将其留给读者作为练习(我总是讨厌数学书上这么说)。


