在这一页
淘汰赛 52
简介
Knockout 52 是一款独特的赌桌,将于 2024 年 5 月在密歇根州巴特尔克里克的 FireKeepers 赌场首次亮相。随后,它计划于 2024 年 5 月 17 日在拉斯维加斯的 Strat 开始现场试验。
没有其他游戏能与之媲美。简而言之,桌上有一个布局,上面有一副牌,牌堆里有13个点数。荷官会一次向布局上的每个位置发一张牌。当牌堆里的一张牌与布局上下一个位置的点数匹配时,游戏停止。如果玩家发出13张、26张或39张牌仍未匹配,则从第一个位置重新开始。目标是正确预测匹配点数或完全不匹配需要多长时间。
规则
- 可以使用任意数量的牌组。本报告中的分析基于一副52张牌的牌组。
- 投注布局应由四行十三列组成。每列应按从左到右的顺序依次标注为“A”到“K”。每行称为一“轮”。
- 下注结束后,荷官将发出第一轮的第一张牌。如果这张牌与牌桌上的点数相同(在本例中为A),则该轮结束,并判定投注获胜。
- 否则,如果第一张牌不是A,则将发第二张牌给第一轮玩家。如果这张牌与牌型上的点数相同,在本例中为2,则该轮结束,并判定投注结果为赢。
- 第一轮的发牌过程将持续进行,直到有一张牌与列标题匹配,或者 13 张牌中没有一张与各自的列标题匹配。
- 如果第一轮没有出现相同点数,荷官将在第二轮发第14张牌到A列。如果该牌不是A,荷官将在第二轮继续发牌,直到该轮结束或出现相同点数。
- 如果前26张牌没有相同的点数,荷官将以相同的方式发出第三轮牌。如果第三轮牌中没有相同的点数,荷官将进入最后的第四轮。
- 如果庄家发完所有 52 张牌而没有一张匹配,则称为“无匹配”,并且无匹配的赌注将被裁定(此事件中不会有其他获胜者)。
- 所有赌注的输赢取决于行和/或列中第一个匹配或根本没有匹配。
- 有以下类型的投注可供选择:
- 第一轮——第一场比赛将在第一轮进行。获胜赔率为1赔2。
- 第二轮——第一场比赛将在第二轮进行。获胜赔率为3比1。
- 第三轮——第一场比赛将在第三轮进行。获胜赔率为10比1。
- 第四轮——第一场比赛将在第四轮进行。获胜赔率为30比1。
- 无比赛——四轮均无比赛获胜赔率为 50 比 1。
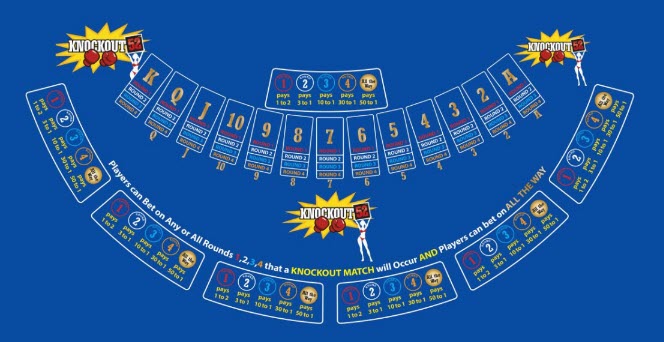
Knockout 52 布局
分析
下表展示了我假设一副牌的分析。右栏显示最佳投注是第一轮,庄家优势为3.56%。
单副牌分析
| 赌注 | 支付 | 可能性 | 庄家优势 |
|---|---|---|---|
| 第一轮 | 0.5 | 0.643070 | 0.035395 |
| 第二轮 | 3 | 0.229534 | 0.081865 |
| 第三轮 | 10 | 0.081924 | 0.098832 |
| 第四轮 | 三十 | 0.029240 | 0.093557 |
| 无匹配 | 50 | 0.016232 | 0.172189 |
以下是我根据八副牌进行的分析。
八副牌分析
| 赌注 | 支付 | 可能性 | 庄家优势 |
|---|---|---|---|
| 第一轮 | 0.5 | 0.646281 | 0.030579 |
| 第二轮 | 3 | 0.228605 | 0.085579 |
| 第三轮 | 10 | 0.080858 | 0.110560 |
| 第四轮 | 三十 | 0.028602 | 0.113344 |
| 无匹配 | 50 | 0.015654 | 0.201637 |
下表显示了一副牌和八副牌中任意给定数量的牌匹配或不匹配的概率。
详细分析
| 发牌 | 一副甲板 | 八副牌 |
|---|---|---|
| 1 | 0.076929 | 0.076927 |
| 2 | 0.070886 | 0.070991 |
| 3 | 0.065338 | 0.065518 |
| 4 | 0.060230 | 0.060465 |
| 5 | 0.055538 | 0.055805 |
| 6 | 0.051209 | 0.051513 |
| 7 | 0.047222 | 0.047543 |
| 8 | 0.043560 | 0.043882 |
| 9 | 0.040178 | 0.040502 |
| 10 | 0.037071 | 0.037382 |
| 11 | 0.034204 | 0.034504 |
| 12 | 0.031568 | 0.031849 |
| 十三 | 0.029135 | 0.029399 |
| 14 | 0.027456 | 0.027209 |
| 15 | 0.025301 | 0.025108 |
| 16 | 0.023325 | 0.023177 |
| 17 | 0.021499 | 0.021388 |
| 18 | 0.019824 | 0.019743 |
| 19 | 0.018278 | 0.018220 |
| 20 | 0.016856 | 0.016815 |
| 21 | 0.015547 | 0.015522 |
| 22 | 0.014344 | 0.014330 |
| 23 | 0.013232 | 0.013223 |
| 24 | 0.012209 | 0.012204 |
| 二十五 | 0.011266 | 0.011266 |
| 二十六 | 0.010399 | 0.010399 |
| 二十七 | 0.009800 | 0.009622 |
| 二十八 | 0.009032 | 0.008883 |
| 二十九 | 0.008323 | 0.008197 |
| 三十 | 0.007672 | 0.007565 |
| 31 | 0.007074 | 0.006982 |
| 三十二 | 0.006523 | 0.006444 |
| 33 | 0.006016 | 0.005948 |
| 三十四 | 0.005549 | 0.005489 |
| 三十五 | 0.005121 | 0.005067 |
| 三十六 | 0.004723 | 0.004678 |
| 三十七 | 0.004359 | 0.004318 |
| 三十八 | 0.004021 | 0.003985 |
| 三十九 | 0.003712 | 0.003679 |
| 40 | 0.003497 | 0.003404 |
| 41 | 0.003223 | 0.003142 |
| 四十二 | 0.002971 | 0.002899 |
| 43 | 0.002739 | 0.002677 |
| 四十四 | 0.002526 | 0.002469 |
| 45 | 0.002330 | 0.002280 |
| 46 | 0.002147 | 0.002103 |
| 四十七 | 0.001981 | 0.001941 |
| 四十八 | 0.001826 | 0.001793 |
| 49 | 0.001685 | 0.001655 |
| 50 | 0.001556 | 0.001528 |
| 51 | 0.001435 | 0.001410 |
| 52 | 0.001324 | 0.001302 |
| 无匹配 | 0.016232 | 0.015654 |
| 全部的 | 1.000000 | 1.000000 |
方法论
我们用随机模拟来分析这款游戏。对于一副牌,模拟了4,910,000,000局游戏。对于八副牌,模拟了8,899,500,000局游戏。我觉得概率精确到小数点后五位。
外部链接
我在 Wizard of Vegas 论坛上讨论Knockout 52。


