视频扑克 - 一般通用
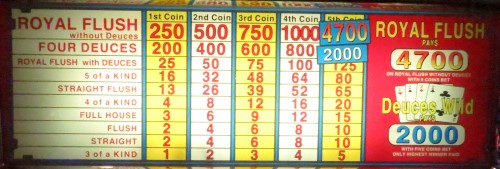
我在玩一台8/5的奖励机,除了正常的四张2、3、4和A的奖励机制外,如果出现同花大顺,奖金为1,199美元;如果出现四张8,奖金将翻倍。我需要我的老虎机卡和最大数量的硬币才能玩。这是否是100%+的奖励机制?
1199美元的赔付金额颇为诱人,略低于赌场必须向美国国税局申报的1200美元上限。Winpoker 6软件可以分析定制游戏。在本例中,回报率高达100.0079%。
视频扑克游戏,无论是JJ、Better还是任何Wild版本,玩起来像一副真正的扑克牌吗?换句话说,机器正面的赔付表决定了这台机器的具体赔付,还是可以通过电脑芯片进行内部修改,使赔付表变得毫无意义?我一直觉得这种说法不靠谱,直到我在《Strictly Slots》杂志上读到一篇文章,说确实存在这种说法,而且可以做到。如果真是这样,你可以并排放置两台相同的视频扑克机,它们拥有不同的庄家优势。我知道赌场可以这样做,就像普通老虎机一样。如果是这样,那么多年来我在杂志、软件和书籍中看到的那些关于赔付表的VP赔付百分比就毫无意义了。
我非常有信心,任何一家值得信赖的电子扑克机制造商都会确保其公平准确。市面上是否存在不诚实的机器或筹码?当然。我很想读一下你提到的那篇文章。
我正在考虑访问你们广告商的网站,以确保他们继续支持你们为博彩公众提供免费建议。你们的网站很棒。我的问题是:在视频扑克中,有可能抽到和打出的牌相同的牌吗?密歇根州博彩控制委员会给了我一个半答案,说所有事件都是由随机数生成器决定的。其次,在VP游戏中,中彩牌的概率是否会像老虎机一样受到赌场的操纵,因为老虎机也由随机数生成器控制。
感谢您的支持。我鼓励大家点击横幅广告来支持本网站。回答您的问题:不,不可能再次获得相同的牌。这台机器代表了从一副牌中公平发牌。一旦您弃牌,就无法再次获得相同的牌。回答第二个问题:不,赌场无法改变每手牌的概率。视频扑克机公平地进行游戏。您获得每手牌的概率取决于随机抽牌和您的游戏技巧。
在密西西比州,视频扑克的法律是否与内华达州相同,即每手牌都是一场新游戏?
我猜你问的是每手牌是否都是从一副新牌里发的,没有之前牌局的记忆。这才是视频扑克应该玩的方式,我相信密西西比也不例外。
你的网络报纸专栏自六月以来就没有更新了。你还好吗?希望如此。我有一张二十一点基本策略卡,非常有用。有没有电子扑克游戏的基本策略卡?谢谢你抽出时间。
我不确定你指的是哪篇网络报纸专栏。不过我没事。其实,你可以在 Custom Strategy Cards 上找到一张我制作的便捷视频扑克策略卡。视频扑克卡可能还没有列出来,但我知道店主有,所以尽管问吧。
更新:定制策略卡业务不再存在。
尊敬的巫师先生,最低回报法律如何影响视频扑克机?如果没有理想的策略,赌场可以安装VP老虎机吗?如果愚蠢的玩家(那些会丢弃一对甚至皇家牌的玩家)的策略导致收益低于州法律规定的x%,他们能起诉赌场吗?最后,出于好奇,假设丢弃同花大顺、保留五张垃圾牌等等,VP老虎机的最低回报率是多少?感谢您宝贵的阅读时间,希望您能回复。
内华达州博彩控制委员会 (Nevada Gaming Control Board) 条例 14.040.1(a) 规定,假设玩家采用最佳策略,游戏设备的回报率必须至少达到 75%。为了回答您的第二个问题,我修改了我的视频扑克程序,使其始终做出最差的玩法。例如,在不赔付的牌型上保留所有五张牌,并弃掉部分或全部的牌型。基于 9/6 J 或更好 (Jacks or Better),此策略的回报率为 2.72%,或赌场优势为 97.28%。以下是完整的回报率表。这样的玩家无法起诉赌场,因为这是他玩得太差的错。
杰克或更好 - 最差的玩家
| 手 | 付清 | 数字 | 可能性 | 返回 |
|---|---|---|---|---|
| 皇家同花顺 | 800 | 48564 | 0.000000 | 0.000002 |
| 同花顺 | 50 | 2058000 | 0.000000 | 0.000005 |
| 四条 | 二十五 | 38040380 | 0.000002 | 0.000048 |
| 客满 | 9 | 292922028 | 0.000015 | 0.000132 |
| 冲洗 | 6 | 336550092 | 0.000017 | 0.000101 |
| 直的 | 4 | 6239759724 | 0.000313 | 0.001252 |
| 三条 | 3 | 12510891616 | 0.000628 | 0.001883 |
| 两对 | 2 | 34968642984 | 0.001754 | 0.003509 |
| 杰克或更好 | 1 | 334574728656 | 0.016785 | 0.016785 |
| 没有什么 | 0 | 19544266875156 | 0.980487 | 0.000000 |
| 全部的 | 19933230517200 | 1.000000 | 0.023717 |
如果您必须选择一款视频扑克游戏进行在线练习(这样您就知道在拉斯维加斯时如何玩),您会选择什么?
如果我把 100 美元的钞票投入回报率为 98% 的视频扑克机并玩到破产,那么我平均总共会下注多少钱?
这个问题有一个简单的公式:初始投资额除以赌场优势。在这个例子中,答案是 100 美元/0.02 = 5000 美元。然而,由于视频扑克的波动性,大多数情况下,这 100 美元撑不了这么久。
对我们这些康涅狄格州的玩家,你们有什么建议吗?他们有世界上最烂的电子扑克机。在市场并不需要的时候,有什么可行的方法可以迫使赌场改进他们的选择吗?
这就是在几乎没有竞争的环境中会发生的情况。要求赌场提供更好的机器无济于事。如果玩家愿意玩赔率低的游戏,他们为什么要改变呢?你唯一的希望就是写信给康涅狄格州的立法者,要求他们结束该州两家赌场的垄断局面,允许其他赌场参与竞争。
如果您每局下注 50 美元,您会在这两款视频扑克游戏中选择哪一款(假设两款游戏的赔付机制相同,且您每手牌最多下注 5 个硬币):单局下注 10 美元,还是十局下注 1 美元?感谢您抽出时间考虑。
从数学上讲,它们的预期收益当然相同。不过我会选择10倍投注,因为波动性更小,而且我觉得更有趣。
有很多免费的在线视频扑克游戏。但是,我正在寻找一个可以在不连接互联网的情况下运行的版本。您知道有没有可以免费下载的《Jacks or Better》版本,并且运行时不需要连接互联网吗?我找到了一些免费下载的演示版本,但它们在运行时仍然会连接到网站,即使游戏是在本地加载的。只要一个基础的、功能逼真的版本就好了。谢谢。
我相信免费的 Winpoker 演示版能够满足您的需求,而且永远不会过期。您可以在www.zamzone.com下载。
视频扑克的偏度系数是多少?
为了方便其他读者理解,任何随机变量的偏度系数(skew)都用来衡量哪个方向的尾部更长。负偏度意味着最可能的结果位于分布的高端,而极端值则倾向于位于低端。正偏度则相反,最可能的结果位于低端,但极端值倾向于位于高端。负偏度时,平均值小于中位数,正偏度时,平均值大于中位数。您可以在维基百科或许多统计学书籍中找到确切的公式。
粗略地说,偏差度与你在一场游戏中获胜的频率相关。在“Jacks or Better”游戏中,如果你没有拿到皇家牌,大多数情况下,你几个小时内都不会赢钱。而“Double Double Bonus”游戏,由于其四倍赔付,你可以在几个小时后更频繁地赢钱。由于大多数人都会受到认知偏差的影响,输钱的痛苦是赢钱的两倍。人们玩“Double Double Bonus”并非因为他们喜欢这种方差,而是因为这样赢钱的几率更大。下表列出了四种常见视频扑克游戏的一些关键统计数据。值得注意的是,“Jacks or Better”游戏中的偏差度最大。
关键视频扑克统计数据
| 统计 | JoB — 9/6 | BP — 8/5 | DDB — 9/6 | DW — NSUD |
|---|---|---|---|---|
| 返回 | 0.995439 | 0.99166 | 0.989808 | 0.997283 |
| 方差 | 19.514676 | 20.904113 | 41.985037 | 25.780267 |
| 倾斜 | 147.114643 | 134.412152 | 66.495372 | 101.23991 |
| (过量)峰度 | 26,498 | 23,202 | 6,679 | 14,550 |
JoB — 9/6 = 全薪Jacks or Better
BP — 8/5 = 标准支付奖金扑克
DDB — 9/6 = 标准赔付双倍奖金扑克
DW — NSUD =“不那么丑的鸭子” Deuces Wild
了解这一点实际上如何帮助视频扑克玩家?我想有人会说,偏度较大的游戏在几个小时的游戏中输钱的可能性更大。例如,在“Jacks or Better”游戏中,如果你没有打出任何皇家牌,赌场优势最终可能会耗尽你的资金。然而,在像“Deuces Wild”或“Double Double Bonus”这样的游戏中,第二高的奖金就能让你在一局游戏中摆脱困境。换句话说,偏度会阻止你在没有打出皇家牌时获胜。了解偏度不会增加你的胜率,但了解预期结果在心理上会有所帮助。所以,下次你在9/6 Jacks游戏中输钱时,就把责任推到偏度上吧。
感谢 Jeff B. 对此问题的帮助。
我在大西洋城玩视频扑克,我敢发誓,有时候我拿到的牌和我在抽牌时打出的牌一模一样。如果机器把打出的牌放回牌堆,对赔率会有什么影响?
Cryptologic 的互联网赌场有这样一款游戏,叫做Bonus Video Poker ,玩家将弃牌放回牌堆。这款游戏的 40-20-9-6 Jacks or Better 赔率表的回报率为 95.2642%,这还不包括重抽奖金功能(我这里就不细说了)。在传统的视频扑克中,该赔率表的回报率为 98.2534%。因此,在这个例子中,将弃牌放回牌堆会让玩家损失近 3%。然而,我非常怀疑这是否真的发生在大西洋城的机器上。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
哪种视频扑克游戏提供赢得皇家奖杯的最佳机会?
我们先来看看一些实用的电子扑克游戏。下表按从高到低的顺序列出了皇家牌的概率。此表未计算百搭皇家牌,因为其赔率远低于自然牌。
视频扑克皇家概率
| 游戏 | 可能性 | 逆 |
|---|---|---|
| 17-7 Joker 扑克 | 0.0000259892 | 38,478 |
| 8-5 红利扑克 | 0.0000248551 | 40,233 |
| 9-6 杰克 | 0.0000247583 | 40,391 |
| 9-6 双倍奖金 | 0.0000245102 | 40,799 |
| 9-6 红利扑克豪华版 | 0.0000237661 | 42,077 |
| “全额支付”双鬼牌 | 0.0000220839 | 45,282 |
| 10-7 双倍奖金 | 0.0000208125 | 48,048 |
令人惊讶的是,Joker Poker 最有可能凑成皇家牌。这让我很惊讶,因为它有一张额外的牌,无法凑成皇家牌。
接下来,我们来看一些非标准的视频扑克游戏。
在 9-6 Jacks Royal Draw中,赔率是 12,178 比 1。
在7-5 Jacks Second Chance Royal中,赔率为1/10,827。这包括“第二次机会”皇家,赔率仅为200。
最后,我认为值得一提的是三倍双倍奖金 (Triple Double Bonus),四张 A 加一张 2-4 踢脚牌,每枚硬币的赔率与皇家同花顺相同,为 800。根据 9-7 赔率表,任何一张 800 的赔率均为 1/10,823。更棒的是皇家 Aces 奖金扑克 (Royal Aces Bonus Poker) ,任何一张皇家同花顺或四张 A 的赔率均为 800,即 800 的赔率仅为 1/3,673。
然而,综合考虑所有因素,我认为皇家同花顺出现概率最高的游戏是“追逐皇家同花顺” 。根据9-6 J的赔率表,皇家同花顺出现的概率是9,084分之一。
为什么 19,933,230,517,200 这个数字在视频扑克的总组合数中出现得如此频繁?
为了其他读者的利益,这里是 9-6 Jacks or Better 的回报表。
“9-6”杰克或更好
| 手 | 付清 | 组合 | 可能性 | 返回 |
|---|---|---|---|---|
| 皇家同花顺 | 800 | 493512264 | 0.00002476 | 0.01980661 |
| 同花顺 | 50 | 2178883296 | 0.00010931 | 0.00546545 |
| 四条 | 二十五 | 47093167764 | 0.00236255 | 0.05906364 |
| 客满 | 9 | 229475482596 | 0.01151221 | 0.10360987 |
| 冲洗 | 6 | 219554786160 | 0.01101451 | 0.06608707 |
| 直的 | 4 | 223837565784 | 0.01122937 | 0.04491747 |
| 三条 | 3 | 1484003070324 | 0.07444870 | 0.22334610 |
| 两对 | 2 | 2576946164148 | 0.12927890 | 0.25855780 |
| 杰克或更好 | 1 | 4277372890968 | 0.21458503 | 0.21458503 |
| 没有什么 | 0 | 10872274993896 | 0.54543467 | 0 |
| 全部的 | 19933230517200 | 1 | 0.99543904 |
我的大多数 52 张牌游戏的视频扑克回报表都有相同数量的组合,即 19933230517200。问题是为什么?
首先,从 52 张牌中选择 5 张牌共有(52,5) = 2,598,960 种方法。
其次,根据玩家弃牌的数量,抽牌组合最多有 combin(47,5) = 1,533,939 种。下表第二列显示了根据弃牌数量计算出的抽牌组合数。
抽奖组合
| 丢弃 | 组合 | 重量 | 产品 |
|---|---|---|---|
| 0 | 1 | 7,669,695 | 7,669,695 |
| 1 | 四十七 | 163,185 | 7,669,695 |
| 2 | 1,081 | 7,095 | 7,669,695 |
| 3 | 16,215 | 473 | 7,669,695 |
| 4 | 178,365 | 43 | 7,669,695 |
| 5 | 1,533,939 | 5 | 7,669,695 |
第二列数字的最小公倍数是 7,669,695。这个数字可以表示为 5×combin(47,5)。为了保持每手牌的组合总数相同,我对听牌组合进行了加权,使听牌组合总数为 7,669,695。
因此,19,933,230,517,200 = combin(52,5)×combin(47,5)×5。我的一些52张牌的视频扑克牌桌的组合数较少。这是因为有时最终回报表中每手牌的组合总数的最大公约数大于1。在这种情况下,我有时会将每个总数除以最大公约数。我的视频扑克分析器会自动执行此操作。
这个问题是在我的“拉斯维加斯巫师”论坛上提出并讨论的。
D赌场真的取消了他们的101.60%松散度的Deuces游戏吗?我记得你说过那是拉斯维加斯最松散的电子扑克机。如果传言属实,现在哪台机器是第一名?
是的,那台机器已经不存在了。正如你所指出的,之前排名第二的游戏现在上升到了第一的位置。那是埃尔科特斯赌场的一款双倍双骰游戏,赔率高达100.92%。完整的赔率表是940-400-25-16-13-4-3-2-2-1。你可以在赌场北端的老虎机房里找到它,那里摆满了老式的阴极射线原机。这是我站在它旁边的照片。

如果你想知道,Loose Deuces 和 Double Deuces 之间的区别在于前者为四个 2 支付 500,而后者为 400。
我知道视频扑克中有些牌型,两种打法和最佳打法一样好。例如,如果玩家拿到了全额赔付的Deuces Wild牌型中的两对,那么他应该只保留一对,保留哪一对都无所谓。我的问题是,是否存在三种打法和正确打法一样好的情况?
是的!在百搭扑克游戏中,如果手牌是垃圾牌,一般来说,最好保留一张最有可能组成顺子或同花的中间牌。然而,有时情况非常危急,甚至平局,这时最好保留的牌才是最好的。
例如,在两对百搭牌扑克牌局中,以及一张QH、10D、5D、7C和2C的97.19%赔率表中,最佳玩法是只持有10D、5D和7C,三张牌都持有的预期赔率为0.240703。这可以用我的视频扑克牌局分析器来验证。
以下是针对同一 Joker 扑克赔率表的其他类似玩法:
- 快速控制 10S 5D 7H 2C
- QH 10D 5D 7H 2C
- KH 10D 5D 8C 3C
- KC 10S 5D 8H 3C
- KH 10D 5D 8H 3C
感谢 Gary Koehler 对此问题的帮助。
你好。我写这封信是因为我是视频扑克的忠实粉丝(虽然我不是赌徒,纯粹是为了好玩而玩模拟游戏)。我想尝试一些模拟游戏,发现你的“我的视频扑克分析方法”页面非常有帮助。虽然我尝试了好几次才真正理解,但我最终还是编写了一个小型模拟器来自动玩游戏,并可以将我的结果与你的视频扑克牌局分析器页面进行比较,得到相同的答案。
但是方法论页面只处理标准的52张牌,没有百搭牌。我尝试自行扩展算法,允许在牌堆中添加1到4张百搭牌,但目前为止,结果既慢又不准确。部分原因在于,由于我的算法用52种可能性代替了百搭牌,百搭牌似乎增加了不少复杂性,而且我认为算法不允许重复索引。我想知道方法论页面是否可以扩展,提供一些处理百搭牌情况的技巧,就像它处理标准牌堆时一样高效。
我很喜欢这个网站,也非常感谢它一直以来提供的帮助,如果没有它,我想我根本无法完成我的项目。祝您拥有美好的一天!
谢谢大家的善意言辞!
循环使用所有52种使用百搭牌的方法肯定会很慢,尤其是在有多张百搭牌的情况下。以下是我使用百搭牌的得分方法:
- 如果您拥有天然同花大顺,则按此评分。
- 否则,计算手中百搭牌的数量。
- 然后根据这个数字和其他牌的数值来对手牌进行评分。
例如,假设你知道你有两张百搭牌。你可以使用以下伪代码,根据其他三张牌来计算牌局得分:
- 如果三张牌都是同花色的,并且最低的一张牌至少为 10,那么您就拥有了一张皇家牌。
- 否则,如果三张牌是同花色的,并且最大和最小的牌之间的差值小于或等于四,那么您就拥有同花顺。
- 否则,如果三张牌都是同花色的,最大的一张是 A,第二大的一张是 5 或更小,那么您也拥有同花顺 (A2345)。
- 否则,如果您有一对,那么您就有四张同点牌。
- 否则,如果三张牌都是同花色,则您有同花。
- 否则,如果最大和最小之间的差值小于或等于 4,则您拥有顺子。
- 否则,如果最高牌是 A,而第二高牌是 5 或更小,那么您也有一个顺子(A2345)。
- 否则,您就有一对。
您已经拥有无百搭牌的代码,因此您必须为 1 到 4 或 5 个百搭牌编写单独的代码,具体取决于您是否希望分析Deuces 和 Joker Wild 。
我知道有个促销活动,13个等级的牌全部拿到四张同点牌就能获得奖金。平均需要多少手牌才能达到这个水平?
让我们看看视频扑克的黄金标准,9-6 Jacks or Better来回答您的问题。
第一步是修改我的计算器,使其包含所有13种四类赔付的明细项目。修改后的收益表如下:
修改后的 Jacks 或 Better 回报表
| 事件 | 支付 | 组合 | 可能性 | 返回 |
|---|---|---|---|---|
| 皇家同花顺 | 800 | 493,512,264 | 0.000025 | 0.019807 |
| 同花顺 | 50 | 2,178,883,296 | 0.000109 | 0.005465 |
| 四A | 二十五 | 3,900,253,596 | 0.000196 | 0.004892 |
| 四K | 二十五 | 3,904,533,816 | 0.000196 | 0.004897 |
| 四问 | 二十五 | 3,898,370,196 | 0.000196 | 0.004889 |
| 四J | 二十五 | 3,886,872,684 | 0.000195 | 0.004875 |
| 四个10 | 二十五 | 3,471,687,732 | 0.000174 | 0.004354 |
| 四个9 | 二十五 | 3,503,226,684 | 0.000176 | 0.004394 |
| 四个8 | 二十五 | 3,504,128,652 | 0.000176 | 0.004395 |
| 四个7 | 二十五 | 3,504,825,252 | 0.000176 | 0.004396 |
| 四6 | 二十五 | 3,504,861,888 | 0.000176 | 0.004396 |
| 四五 | 二十五 | 3,504,895,944 | 0.000176 | 0.004396 |
| 四4 | 二十五 | 3,504,032,676 | 0.000176 | 0.004395 |
| 四3 | 二十五 | 3,503,177,148 | 0.000176 | 0.004394 |
| 四2 | 二十五 | 3,502,301,496 | 0.000176 | 0.004393 |
| 客满 | 9 | 229,475,482,596 | 0.011512 | 0.103610 |
| 冲洗 | 6 | 219,554,786,160 | 0.011015 | 0.066087 |
| 直的 | 4 | 223,837,565,784 | 0.011229 | 0.044917 |
| 三条 | 3 | 1,484,003,070,324 | 0.074449 | 0.223346 |
| 两对 | 2 | 2,576,946,164,148 | 0.129279 | 0.258558 |
| 杰克或更好 | 1 | 4,277,372,890,968 | 0.214585 | 0.214585 |
| 没有什么 | 0 | 10,872,274,993,896 | 0.545435 | 0.000000 |
| 全部的 | 19,933,230,517,200 | 1.000000 | 0.995439 |
获得任意四张同点牌的概率为 0.002363。
下一个需要回答的问题是,平均需要多少次四张牌才能凑齐全部13种组合?为了回答这个问题,我创建了预期试验次数计算器。使用时,请在前13个单元格中输入每种四张牌的组合次数。计算器会告诉你,平均需要41.532646次四张牌才能凑齐全部13种组合。
因此,获得全部 13 张四条所需的预期手数为 41.341739/0.002363 = 17,580。
在Multi-Strike 扑克中不玩全部四条线的代价是什么?
我们以8-5 Bonus Poker为例,下表显示了按投注线数计算的回报。
- 4行:99.375%
- 3行:99.279%
- 2行:99.214%
- 1行:99.166%
下一个列表根据玩的线数显示了不玩最大线数的成本。
- 4行:0.000%
- 3行:0.095%
- 2行:0.160%
- 1行:0.209%
您是否知道,在红利扑克游戏中,如果发出的四张牌都是五张单张牌,最小的一张是4,其他三张都小于J,并且没有顺子或同花的机会,那么梦幻牌视频扑克游戏不会给出正确的梦幻牌。正确的梦幻牌应该是4,因为四张4的牌有额外赢取。然而,给出的梦幻牌可能是其他等级的牌。假设玩家总是接受这张错误的梦幻牌,那么它的代价是什么?
是的,我知道这一点。为了方便其他读者,在梦幻牌游戏中,游戏有时会根据随机发的前四张牌,给出最佳的第五张牌。在红利扑克游戏中,获得梦幻牌的概率是46.7%。玩家可以随时拒绝建议的梦幻牌,换成牌堆中剩余的任何其他牌。不过,据我所知,除了红利扑克的这种情况外,这个建议总是正确的。
如果玩家拿到梦想牌,那么其他四张牌出现这种情况的概率是1.49%。考虑到梦想牌出现的概率为46.7%,这种情况发生的概率为0.70%,即每144手牌出现一次。
使用我的视频扑克牌局分析器,8/5 Bonus Poker 中一对 4 的预期值为 0.855134。一对 5 到 10 的预期值为 0.813506。因此,假设玩家接受梦想牌,每次该漏洞发生时,其预期成本为 0.041628。
游戏回报的总体成本为 0.006955 × 0.041628 = 0.000290,约占 0.03%。
如果玩家总是抽到同花大顺,那么抽到同花大顺的概率是多少?假设玩家总是选择已经抽到最多张同花大顺的花色。
下表显示了在发牌时出现 0 到 5 张皇家牌的概率(假设玩家总是选择已经拥有最多皇家牌的花色)、完成皇家牌的概率以及乘积。
皇家或无玩家
| 皇家卡 在交易中 | 交易 可能性 | 可能性 皇家完整版 | 产品 |
|---|---|---|---|
| 0 | 0.61538462 | 0.00000261 | 0.00000160 |
| 1 | 0.35444947 | 0.00003064 | 0.00001086 |
| 2 | 0.02835596 | 0.00070472 | 0.00001998 |
| 3 | 0.00173608 | 0.01057082 | 0.00001835 |
| 4 | 0.00007234 | 0.11627907 | 0.00000841 |
| 5 | 0.00000154 | 1.00000000 | 0.00000154 |
| 全部的 | 1.00000000 | 0.00006075 |
右下角单元格显示“要么同花大顺,要么全无”的玩家拿到同花大顺的概率为 0.000006075,即 16,461 分之一。
如果玩家可以提前看到下一张牌,那么在视频扑克中出现同花大顺的概率是多少?
假设游戏随机抽取五张牌,这些牌会排成队列等待玩家丢弃。例如,如果玩家丢弃三张,他将获得队列中的后三张。顺便说一句,如果每张牌都对应一张特定的牌,答案也是一样的。下表显示了每张牌中每个数字的皇家点数的概率、抽牌时完成该点数的概率以及乘积。右下角单元格显示总体概率为 0.00006075,相当于 16,461 分之一。
视频扑克中的完美窥视者
| 皇家卡 在交易中 | 交易 可能性 | 可能性 皇家完整版 | 产品 |
|---|---|---|---|
| 0 | 0.61538462 | 0.00000261 | 0.00000160 |
| 1 | 0.35444947 | 0.00003064 | 0.00001086 |
| 2 | 0.02835596 | 0.00070472 | 0.00001998 |
| 3 | 0.00173608 | 0.01057082 | 0.00001835 |
| 4 | 0.00007234 | 0.11627907 | 0.00000841 |
| 5 | 0.00000154 | 1.00000000 | 0.00000154 |
| 全部的 | 1.00000000 | 0.00006075 |
您在解释视频扑克拉片机时举了这样的例子:“即使这款游戏看起来像五张牌的抽牌视频扑克游戏,你的结果也是注定的。比如,如果你在发牌时拿到了同花大顺,然后把所有牌都扔掉,你抽牌时还能拿到另一张同花大顺。” 我的问题是,如果你扔掉一些牌,导致无法得到预定的结果(比如在 Deuces Wild 游戏中,如果是 4 点 2,结果变成了 2;或者在 Double Bonus 游戏中,如果是 4 点 4,结果变成了 1 点,结果变成了 1 点,会发生什么情况?)也许这些类型的游戏并不提供,只有像 Jacks or Better 这样的游戏才不提供这种情况?
我听说会发生这样的事:一位仙女会来,把你抽牌时的手牌变成你原本注定的牌。比如,如果你注定在发牌时拿到两张2,抽牌后会变成四张2,如果你把2扔掉,你很可能会在抽牌时自然而然地拿到另外两张,然后仙女会把你扔掉的两张2改成两张垃圾牌。
在视频扑克中,发牌后玩家有多少次会拿到 0 到 5 张皇家牌?
答案相当复杂,因为玩家在发牌后,有多种方式可能在多个花色中出现皇家牌。我假设玩家总是保留最有可能出现皇家牌的花色的牌,并在两张或两张以上花色相同的情况下任意抽取。话虽如此,让我来定义一些缩写:
- 皇家牌 = 等级 10 到 A 的牌。
- H = 红桃皇家牌。
- S = 红桃皇家牌。
- C = 红桃皇家牌。
- D = 红桃皇家牌。
- x = 非皇家卡
下表列出了每种可能情况的组合数。一行将包含所有数学上等价的情况。例如,Hxxxx 将包含任意花色(不仅仅是红桃)中只有一张皇家牌的情况。
交易后与皇家合并
| 手 | 皇家卡 | 组合 |
|---|---|---|
| 哈哈哈哈 | 5 | 4 |
| 哈哈哈 | 4 | 300 |
| 哈哈哈 | 4 | 640 |
| 卫生保健服务部 | 3 | 1,200 |
| 霍华德健康科学中心 | 3 | 3,000 |
| 霍奇金淋巴瘤 | 3 | 19,200 |
| 哈哈哈 | 3 | 19,840 |
| 卫生与健康科学中心 | 2 | 6,000 |
| 卫生和健康服务部 | 2 | 19,200 |
| 卫生与公众服务部 | 2 | 5,000 |
| 高速钢 | 2 | 96,000 |
| HHSxx | 2 | 297,600 |
| 哈哈哈 | 2 | 198,400 |
| HSCDx | 1 | 2万 |
| 高速串行总线 | 1 | 248,000 |
| HSxxx | 1 | 744,000 |
| 哈 | 1 | 719,200 |
| xxxxx | 0 | 201,376 |
| 全部的 | 2,598,960 |
下表显示了发牌后出现 0 到 5 张皇家牌的总体概率。
皇家概率卡
| 皇家卡 | 可能性 |
|---|---|
| 5 | 0.0002% |
| 4 | 0.0362% |
| 3 | 1.6637% |
| 2 | 23.9403% |
| 1 | 66.6113% |
| 0 | 7.7483% |
| 全部的 | 100.0000% |
并不是你问的,但是如果玩家遵循“要么皇家要么什么都没有”的策略,那么他每手拿到皇家的概率将是 23,162 分之一。
如果我使用完美的投注策略来玩视频扑克,哪个游戏能让我获得同花大顺的最佳机会?
作为比较基础,假设采用最佳策略,传统视频扑克中出现同花大顺的概率约为 1/40,000 到 1/45,000。以下是一些随机选择的游戏的具体数字:
- 9-6 J 或更好:40,391 分之一
- 25-15-9-4-4-3(伊利诺伊州) Deuces Wild — 43,423 分之一
- 9-7 三倍奖金:45,358 分之一
对于渴望皇家牌的玩家来说,在Chase the Royal中,概率会显著上升。这是早期的视频扑克变体,玩家可以在发牌时将一对人头牌换成三张同花大顺。为了使交易更有价值,如果您切换,游戏会增加顺子和同花的赢率。确切的皇家概率取决于基础游戏和赔率表。在三倍红利和 8-5 赔率表的基础游戏中,概率最大,皇家概率为 9,151 分之一。这包括抽牌中的皇家牌,1 赔 800,概率为 9,282 分之一,以及发牌中的皇家牌,1 赔 2000,概率为 649,773 分之一。
然而,如果考虑到玩家必须支付相当于基本赌注的费用才能启用某项功能的游戏,情况会更加乐观。在“Dream Card Draw Poker” (不要与“Dream Card Poker”混淆)中,玩家通常会拿到自己梦寐以求的牌(假设是数学家在做梦)作为第五张牌。在“Jacks or Better”游戏中,“Dream Card”出现的概率最高,为50.5%。在“9-6 Jacks or Better”游戏中,“Royal”(皇家)牌的总出现频率为8,105分之一。请记住,由于启用该功能需要支付费用,皇家牌的实际赢利会降至1分之400。
只要我提到梦幻牌扑克(一款不同于梦幻牌抽牌扑克的游戏),皇家牌的出现频率就没那么高。皇家牌在11-8-6 Js or Better游戏中出现的频率最高,为1/15,034。
这个答案没有考虑“Movin' On Up Poker”这个古老而鲜为人知的电子扑克游戏,玩家可以抽两到三次,而不是一次。我不知道这款游戏中的“皇家频率”,但在“三次抽奖”中,玩家必须支付相当于其基本赌注五倍的费用才能获得额外的两次抽奖,我粗略估计这个概率大约是四千分之一。
总而言之,如果不算那些玩家必须支付额外费用才能使用某种噱头的游戏,我的答案就是《追逐皇家》。
如果我采用“伊利诺伊州双打”游戏中“不那么丑小鸭”的最佳策略,玩家失误的代价是多少?
提醒一下,以下是提到的支付表:
不那么丑的小鸭子:1-2-3-4-4-10-16-25-200-800。
伊利诺伊州平分:1-2-3-4-4-9-15-25-200-800
接下来,这是“不那么丑小鸭”的回报表,遵循该游戏的最佳策略。
不那么丑的小鸭子——正确的策略
| 事件 | 支付 | 组合 | 可能性 | 返回 |
|---|---|---|---|---|
| 天然皇家同花顺 | 800 | 458,696,304 | 0.000023 | 0.018409 |
| 四张 2 | 200 | 3,721,737,204 | 0.000187 | 0.037342 |
| 狂野皇家同花顺 | 二十五 | 38,006,962,464 | 0.001907 | 0.047668 |
| 五张相同的牌 | 16 | 61,961,233,656 | 0.003108 | 0.049735 |
| 同花顺 | 10 | 102,392,435,976 | 0.005137 | 0.051368 |
| 四条 | 4 | 1,216,681,289,508 | 0.061038 | 0.244151 |
| 客满 | 4 | 520,566,943,104 | 0.026116 | 0.104462 |
| 冲洗 | 3 | 413,870,908,056 | 0.020763 | 0.062289 |
| 直的 | 2 | 1,142,885,476,800 | 0.057336 | 0.114671 |
| 三条 | 1 | 5,325,911,611,716 | 0.267188 | 0.267188 |
| 没有什么 | 0 | 11,106,773,222,412 | 0.557199 | 0.000000 |
| 全部的 | 19,933,230,517,200 | 1.000000 | 0.997283 |
接下来,这是伊利诺伊州双骰子彩票的赔付表,使用了该赔付表的正确策略。右下角单元格显示赔付为0.989131。
伊利诺伊州平分——正确策略
| 事件 | 支付 | 组合 | 可能性 | 返回 |
|---|---|---|---|---|
| 天然皇家同花顺 | 800 | 459,049,128 | 0.000023 | 0.018423 |
| 四张 2 | 200 | 3,727,422,492 | 0.000187 | 0.037399 |
| 狂野皇家同花顺 | 二十五 | 38,117,987,136 | 0.001912 | 0.047807 |
| 五张相同的牌 | 15 | 62,201,557,608 | 0.003120 | 0.046807 |
| 同花顺 | 9 | 98,365,859,016 | 0.004935 | 0.044413 |
| 四条 | 4 | 1,221,942,888,444 | 0.061302 | 0.245207 |
| 客满 | 4 | 522,030,131,520 | 0.026189 | 0.104756 |
| 冲洗 | 3 | 407,586,633,720 | 0.020448 | 0.061343 |
| 直的 | 2 | 1,145,767,137,120 | 0.057480 | 0.114961 |
| 三条 | 1 | 5,342,397,992,292 | 0.268015 | 0.268015 |
| 没有什么 | 0 | 11,090,633,858,724 | 0.556389 | 0.000000 |
| 全部的 | 19,933,230,517,200 | 1.000000 | 0.989131 |
下表显示了使用“不那么丑小鸭”组合和概率的赔付表,得出的“伊利诺伊双人赛”赔付表的回报率。右下角单元格显示回报率为0.989131。
伊利诺伊州平局——NSUD 策略
| 事件 | 支付 | 组合 | 可能性 | 返回 |
|---|---|---|---|---|
| 天然皇家同花顺 | 800 | 458,696,304 | 0.000023 | 0.018409 |
| 四张 2 | 200 | 3,721,737,204 | 0.000187 | 0.037342 |
| 狂野皇家同花顺 | 二十五 | 38,006,962,464 | 0.001907 | 0.047668 |
| 五张相同的牌 | 15 | 61,961,233,656 | 0.003108 | 0.046627 |
| 同花顺 | 9 | 102,392,435,976 | 0.005137 | 0.046231 |
| 四条 | 4 | 1,216,681,289,508 | 0.061038 | 0.244151 |
| 客满 | 4 | 520,566,943,104 | 0.026116 | 0.104462 |
| 冲洗 | 3 | 413,870,908,056 | 0.020763 | 0.062289 |
| 直的 | 2 | 1,142,885,476,800 | 0.057336 | 0.114671 |
| 三条 | 1 | 5,325,911,611,716 | 0.267188 | 0.267188 |
| 没有什么 | 0 | 11,106,773,222,412 | 0.557199 | 0.000000 |
| 全部的 | 19,933,230,517,200 | 1.000000 | 0.989038 |
错误成本是伊利诺伊 Deuces 的最佳回报(第二个表)减去使用 NSUD 策略的伊利诺伊 Deuces 的回报(第三个表)= 0.989131 - 0.989038 = 0.000093。
我在《维加斯巫师》杂志上读到您关于可逆皇家牌局的文章,它的回报率高达 105.22% 。这个回报率假设了最佳策略,包括牌序。如果我假设皇家牌局获胜率一般,回报率是多少?如果我使用普通的 6-5 Bonus Poker 策略(基本赔付表)呢?
假设策略无偏差,每60个皇家牌中会有1个连续出现。可逆皇家大奖的赔率为161,556/1。其他皇家牌的赔率为1800/1。因此,平均皇家牌中奖金额为(1/60)*161,556 + (59/60)*800 + 17,396/1。
如果我们假设所有皇室成员支付 17,396 并根据皇室胜利采取最佳策略,那么回报率将下降到 103.56%。
如果我们玩标准的 6-5 红利扑克策略,即基本支付表,那么回报率将进一步下降到 101.97%。
在您的视频扑克编程技巧中,您解释了尽管视频扑克中有 2,598,960 种可能的起手牌,但对于一副 52 张牌的扑克牌,只需要分析 134,459 类牌。
我的问题是,小丑扑克有多少个课程?
为此,我向我尊敬的同事 Gary Koehler 求助,他是视频扑克数学方面的专家。以下是他根据百搭牌数量给出的答案:
- 1. 小丑:150,891
- 2张小丑牌:169,078
- 3张小丑牌:189,189
- 4张小丑牌:211,406
- 5张小丑牌:235,925
在您的视频扑克编程技巧中,您解释了尽管视频扑克中有 2,598,960 种可能的起手牌,但在 52 张牌的扑克牌组中,只需分析 134,459 种类型的牌型。我的问题是,如果有人玩的是牌型顺序很重要的游戏,比如Ace$ Bonus Poker或连续皇家牌有累积奖金的游戏,那么需要分析多少种不同类型的牌型?
为此,我向我尊敬的同事Gary Koehler请教,他是视频扑克数学专家。他的答案是15,019,680。
视频扑克抽牌后平均持有多少张牌?
下表显示了10种不同游戏和赔率表的平均持牌数量。所列游戏的平均持牌数量为2.05张。
视频扑克中的平均牌数
| 游戏 | 赔率表 | 返回 | 平均持卡量 |
|---|---|---|---|
| 奖金 Deuces | 10-4-3-3 | 97.36% | 1.845550 |
| 两局狂野 | 25-15-9-5-3 | 100.76% | 1.926010 |
| 白热王牌 | 9-5 | 99.57% | 2.055630 |
| 超级双倍双倍奖金 | 7-5 | 99.17% | 2.057280 |
| 双倍双倍奖金 | 9-5 | 97.87% | 2.058390 |
| 三倍双倍奖金 | 8-5 | 95.97% | 2.072620 |
| 红利扑克 | 8-5 | 99.17% | 2.080610 |
| 杰克或更好 | 9-5 | 98.45% | 2.081030 |
| 红利扑克豪华版 | 8-5 | 97.40% | 2.150470 |
| 双倍奖金 | 9-6-5 | 97.81% | 2.173550 |
我知道,如果你在老虎机上赢了1200美元或以上,你可以选择支票支付。话虽如此,为了便于讨论,假设我想把现金兑换成赌场签发的支票。假设我完美地玩了9/6 Jacks or Better,面额25美元(或总投注125美元)。如果把现金兑换成支票,我预计会损失多少钱?
对于9-6 J或更好的牌,每拿到四张或更高的牌,您就能赢得1200美元或更多。葫芦及以下的赔率是0.911103。您需要将原始资金翻倍1/(1-0.911103) = 11.249016倍,直到您的现金兑换成支票或输给赌场优势。赌场优势是0.004561。因此,您预计会损失原始资金的0.004561 × 11.249016 = 0.051306倍。
有趣的是,尽管 9-6 双倍奖金的赌场优势更高,但将现金兑换成支票的成本却更低。这款游戏所有四张同花的胜率都更高,所以你的支票金额也更大。在该游戏中,葫芦及以下的回报率为 0.777138。这意味着,你需要将你的资金循环 1/(1-0.777138) = 4.487076 次才能将其兑换成支票。9-6 双倍奖金的赌场优势为 0.010192。因此,兑换成现金的预期损失为 4.487076 × 0.010192 = 0.045733。
您可以通过针对四种及以上类型的策略偏差进一步降低成本,但我将其留给读者作为练习。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
在多人视频扑克游戏中,以 9/6 Jacks or Better 赢得大奖(赢得 1,200 美元或更多)的概率是多少?
当然,这取决于面额和游戏次数。下表显示了这些概率。
多人视频扑克中的累积奖金概率
| 面值 | 3 玩 | 5 玩 | 10 玩 | 25 玩 | 50次播放 | 100次播放 |
|---|---|---|---|---|---|---|
| 0.01 美元 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000001 | 0.000001 |
| 0.05 美元 | 0.000000 | 0.000000 | 0.000001 | 0.000001 | 0.000002 | 0.000022 |
| 0.10 美元 | 0.000001 | 0.000001 | 0.000002 | 0.000006 | 0.000047 | 0.000378 |
| 0.25 美元 | 0.000002 | 0.000003 | 0.000008 | 0.000053 | 0.000369 | 0.000556 |
| 0.50 美元 | 0.000070 | 0.000115 | 0.000238 | 0.000782 | 0.001247 | 0.008527 |
| 1.00 美元 | 0.000070 | 0.000128 | 0.000473 | 0.000786 | 0.009518 | 0.072671 |
| 2.00 美元 | 0.000083 | 0.000363 | 0.000488 | 0.010002 | 0.070029 | 0.239753 |
| 5.00 美元 | 0.000720 | 0.001290 | 0.012978 | 0.100374 | 0.318838 | 0.768839 |
| 25.00 美元 | 0.041494 | 0.124818 | 0.348811 | 0.835708 | 0.995943 | 0.999983 |
该表取自我的视频扑克附录 2 ,其中我展示了玩家在大型模拟中获得每次总胜利的频率。