电视游戏节⺫ - 常问问题
这并不完全是赌博,但我一直想知道在《价格猜猜猜》节目中,当你不最后一个旋转大轮盘时,最佳策略是什么。假设你无法控制旋转结果(完全随机),每次旋转结果为5美分的倍数,从0.05美元到1.00美元。你可以选择旋转一次或两次相加,但不能超过1.00美元。那么,在达到多少金额时,你应该放弃第二次旋转,以便有最大概率击败在你之后旋转的选手?
如果第一位玩家的首次旋转结果是65美分或更少,他应该再旋转一次。
若以下任一条件为真,则第二位玩家应重新旋转。
- 他的分数低于第一位选手的分数。
- 他的得分是50分或更低。
- 他的分数是65分或更低,并且他与第一名玩家并列。
价格猜猜猜 (Price is Right) 游戏中Plinko游戏的最佳策略是什么?
从左到右,奖金分别为 100 美元、500 美元、1000 美元、0 美元、10000 美元、0 美元、1000 美元、500 美元、100 美元。我需要知道棋盘上棋子的确切排列才能进行完美的分析,但仅凭目测棋盘(见上面的链接),我强烈认为玩家应该将冰球直接扔到 10,000 美元的奖金上。虽然它以两个零为界,但其他所有奖金与最高奖金相比都黯然失色。因此,玩家的策略应该是将冰球直接扔到上面,以最大化获得最高奖金的概率。为了证实或否定我的假设,我进行了搜索,发现有很多链接致力于研究这个游戏。这个( www.amstat.org/publications/jse/v9n3/biesterfeld.html )是其中一个比较好的链接,它与我的结论一致。其中部分内容指出,将冰球投到中间的预期价值为 2557.91 美元,投到中间两侧的预期价值为 2265.92 美元,并且随着远离中心而逐渐减少。
在游戏节⺫「Let’s Make a Deal 让我们来做个交易」中, 那⾥有三扇⻔,举例来说, 其中两扇⻔后⾯各有⼀只⼭⽺, 另⼀扇⻔后⾯有⼀部新⻋。节⺫主持⼈Monty Hall会选出两位参赛者来选定⼀扇⻔。每次Monty都会打开⼀扇后⾯有⼭⽺的⻔, 让我们举例这是第⼀位参赛者。虽然Monty从未真的这样做过, 假使Monty在这时给其他参赛者机会去转换⻔的选择、改⽽去打开其他关闭的⻔, 他应该转换选择吗?
是的!这个问题的关键在于, 主持⼈总是会先打开有⼭⽺的⻔。他预先知道哪⼀扇⻔内有汽⻋, 所以⽆论参赛者选哪⼀扇⻔, 他总是能够先打开有⼭⽺的⻔。这个问题被称之为「Monty Hall悖论」, 它常会引起许多困惑、是因为这问题是被设计过的, 它错误地不说清楚主持⼈知道汽⻋藏在哪⾥,并总是在第⼀次就打开有⼭⽺的⻔。我想责备⼀下Marilyn Vos Savant, 她在她的专栏⾥糟糕地设计这个问题。让我们假设奖品就在1号⻔之后。以下是如果参赛者(第⼆位)有个策略不去转换选择的话。
- 参赛者选择1号⻔ --> 参赛者赢
- 参赛者选择2号⻔ --> 参赛者输
- 参赛者选择3号⻔ --> 参赛者输
以下是如果参赛者有个策略去转换选择的话、看看会发⽣什么事。
- 参赛者选择1号⻔ --> 主持⼈打开后⾯有⼭⽺的2或3号⻔ --> 参赛者转换选择其他的⻔ --> 参赛者输
- 参赛者选择2号⻔ --> 主持⼈打开后⾯有⼭⽺的3号⻔ --> 参赛者转换选择1号⻔ --> 参赛者赢
- 参赛者选择3号⻔ --> 主持⼈打开后⾯有⼭⽺的2号⻔ --> 参赛者转换选择1号⻔ --> 参赛者赢
所以参赛者若是不转换选择的话, 他有1/3赢的机会。参赛者若是转换选择的话, 他则有2/3赢的机会。因此参赛者肯定应该要转换选择。
阅读更多关于「Monty Hall悖论」, 我推荐这篇在 维基百科的⽂章。
我的问题是关于一个被称为“双信封悖论”的问题。你正在参加一个游戏节目。你面前有两个信封,每个信封里都装着未知数额的现金。你被告知其中一个信封里的钱是另一个信封的两倍。现在你被要求选择一个信封。你选了一个,里面装着5万美元。现在你被告知你可以保留你选的信封,或者换成另一个。你应该换吗?如果你事先知道你可以换,那么换不换就无所谓了,因为你只需要选择你最终想要的那个信封。但是,因为你是在选择信封之后才知道可以换,所以最初的选择和换信封的选择是两个独立事件,对吗?也就是说,在决定是否换信封时,另一个信封里的钱要么是你当前金额的两倍,要么是你当前金额的一半。所以它要么是10万美元,要么是2.5万美元。由于两种情况发生的概率都是50%,所以另一个信封的预期价值是62,500美元。一般来说,如果我们让 x = 你最初选择的金额,那么另一个信封的期望值就是 1.25 倍。因此,交换总是正确的。这样对吗?谢谢。
我对这个问题非常熟悉。我在我的数学题网站上,也就是第6题里提到过。在那里,我讨论了一般情况,包括完全不查看第一个信封。但是,要回答你的问题,我们不能忽略游戏的场地。你说这是一档“游戏节目”。在大多数游戏节目中,5万美元已经是一笔不错的奖金了。但《价格猜猜猜》(Price is Right)节目中,很少有选手能赢到这么高的奖金。我猜《谁想成为百万富翁》(Who Wants to be a Millionaire)节目中,只有不到50%的选手能赢到这么高的奖金。与此同时,2.5万美元的奖金在游戏节目中并不罕见。在《价格猜猜猜》(Price is Right)节目中,汽车的中奖率通常都在2.5万美元左右。在《谁想成为百万富翁》(Who Wants to be a Millionaire)节目中,3.2万美元的中奖率也很常见。《危险边缘》(Jeopardy)节目中,每档节目的平均奖金大约为2.5万美元。伟大的肯·詹宁斯(Ken Jennings)在74场胜利中,平均只赢了34,091美元。所以,我的观点是,对于游戏节目来说,赢得5万美元已经很不错了,赢得10万美元的概率远低于赢得2.5万美元。因此,作为一名游戏节目鉴赏家,我认为另一个信封里更有可能装2.5万美元,而不是10万美元。所以,我认为在你的例子中,最好保留5万美元。这也表明,你永远不能假设另一个信封里装的是一半或两倍金额的概率恰好是50%。一旦你了解了金额,并结合比赛场地的情况,你就能做出明智的换信封决定,这样1.25倍的论点就不攻自破了。
我的问题是关于一档名为“一掷千金”的游戏节目,这档节目在澳大利亚非常受欢迎,即将登陆英国。节目中,参赛者需要面对26个带编号的公文包,每个公文包里都藏有一定数额的钱,金额从50美分到20万美元不等,具体金额如下。
- 0.50 美元
- 1美元
- 2美元
- 5美元
- 10美元
- 25美元
- 50美元
- 75美元
- 100美元
- 150美元
- 250美元
- 500美元
- 750美元
- 1,000美元
- 1,500美元
- 2,000 美元
- 3,000 美元
- 5,000 美元
- 7,500 美元
- 10,000美元
- 15,000美元
- 3万美元
- 5万美元
- 75,000美元
- 10万美元
- 20万美元
参赛者从中选择一个公文包作为自己的箱子。通过排除法,他们打开其他箱子,试图算出自己的箱子里有多少钱,或者是否更明智地接受“银行出价”。银行出价基于剩余公文包的算术平均值,但不等同于该平均值。因此,如果剩余的公文包大多是高价值的,那么参赛者的公文包很可能很有价值,因此银行出价会很高。相反,如果玩家运气不好,打开了价值更高的公文包,那么银行出价就会很低。如果你是这个游戏的参赛者,最佳策略是什么?一个非数学直觉策略是忽略银行出价,继续打开箱子,直到20万美元被打开并消除,或者10万美元和7.5万美元都被打开并消除。巫师,这个游戏背后的数学原理是什么?
“一掷千金”刚刚在美国开始。规则听起来一样,只是我们的奖金最高可达一百万美元,具体如下。
- 0.01
- 1
- 5
- 10
- 二十五
- 50
- 75
- 100
- 200
- 300
- 400
- 500
- 750
- 1000
- 5000
- 10000
- 25000
- 5万
- 75000
- 100000
- 20万
- 30万
- 40万
- 50万
- 750000
- 1000000
游戏流程如下:
- 玩家为自己选择一个案例
- 玩家打开剩余 25 个箱子中的 6 个。
- 银行家提出报价。
- 如果玩家拒绝,他会再打开剩余 19 个箱子中的 5 个。
- 银行家提出报价。
- 如果玩家拒绝,他会再打开剩余 14 个箱子中的 4 个。
- 银行家提出报价。
- 如果玩家拒绝,他会再打开剩余 10 个箱子中的 3 个。
- 银行家提出报价。
- 如果玩家拒绝,他会再打开剩余 7 个箱子中的两个。
- 银行家提出报价。
- 如果玩家拒绝,他会再打开剩下的一个箱子。
- 不断重复步骤 11 和 12,直到玩家接受报价或玩家拥有最后一个未打开的盒子。
下图描绘了玩家的期望值和银行家的报价。
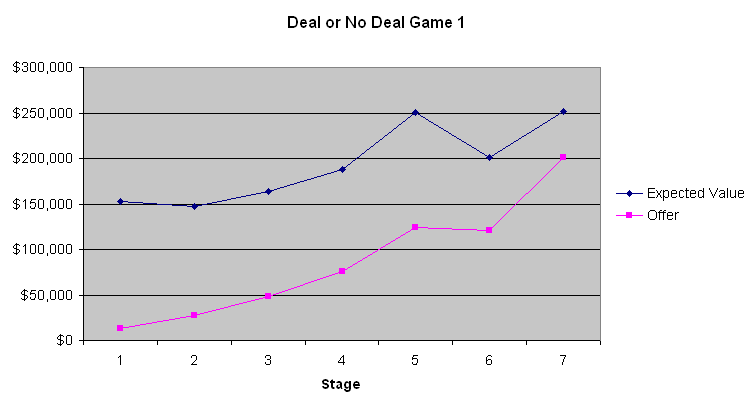
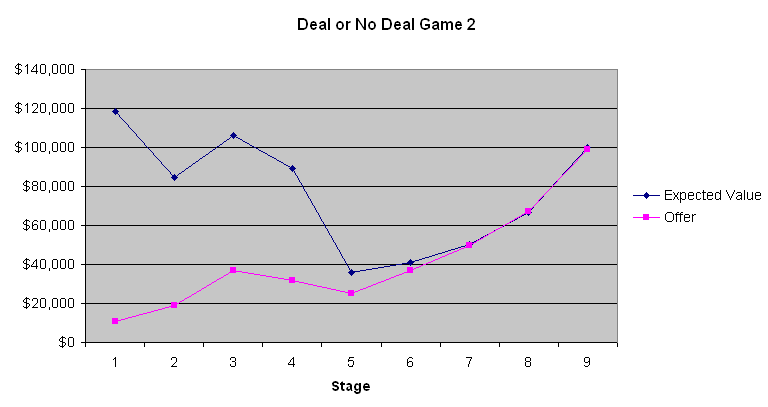
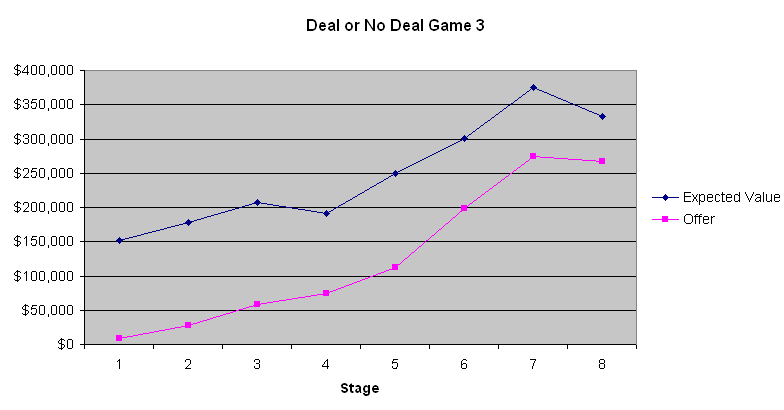
从这三张图表中,最明显的一点是,银行开出的前四到六个出价都很糟糕。平均每个箱子在开箱前有131,477.54美元。第一阶段只出价9000到13000美元,只有傻瓜才会这么做。然而,出价逐渐上升。第二局游戏显示,当玩家的预期值相当低时,预期值在游戏接近尾声时几乎与银行家的出价相同。然而,在第一局和第三局游戏中,当预期值较高时,银行家显然试图利用大多数人在涉及大额赌注时规避风险的天性。我不知道这是否重要,但第二局的参赛者似乎是一个想要大赢的赌徒。根据主持人通过电话与银行家沟通的评论,银行家似乎确实会考虑参赛者的言行举止。如果我是银行家,我也会这么做。
如果玩家既不厌恶风险也不倾向于风险,并且不考虑税务影响,那么玩家应该不断拒绝银行家的报价,直到其中一个报价超过剩余行李箱的平均数。对大多数人来说,所得税法的累进性质有利于接受交易。正如我之前所说,我粗略地说,货币的价值与金额的对数成正比。因此,你投入的财富越多,你就越倾向于冒险拒绝银行家的报价。由于涉及的金额如此之大,没有一种策略适合所有人。不过,我可以相当肯定地说,玩家应该拒绝前四到六个报价,然后根据具体情况(双关语)接受其他报价。
我正在看“一掷千金”。我意识到银行家的“出价”只是箱子剩余价值除以箱子数量(四舍五入)。这游戏有什么策略吗?还是说“一掷千金”总是可以接受的?这取决于你需要开多少箱子还是其他什么?
正如我在2005年12月26日的专栏文章中指出的那样,庄家的出价通常远低于其余情况的平均值。然而,假设情况总是如此,那么每种策略的预期价值都会相同。玩家对每种出价都会无动于衷。
在“一掷千金”游戏开始时,选中 1,000,000 美元案例的概率是 1/26。在排除除 1 之外的所有案例后,我的案例中包含 100 万美元的概率是多少?是 50-50 还是仍然是 1/26?
50-50
您在2006年4月5日的专栏文章中写道,如果“一掷千金”只剩下两个案子,而百万美元仍在进行中,那么我的案子赢得百万美元的概率是五五开。我不同意。这难道不是蒙提霍尔难题的一个变种吗?也就是说,百万美元在舞台上的可能性比在他自己的案子中更大?
不。很多人跟我争论这个问题。很多作者声称,即使引入额外的信息,概率也不会改变。所以,如果概率一开始是1/26,那它就必须保持不变。与博彩系统推销员的说法相反,概率确实会随着额外信息的引入而改变。我不想在这里讲授基本的概率知识,但任何一本关于条件概率或贝叶斯定理的大学数学书都应该很好地涵盖这个主题。
让我来解释一下《让我们做个交易》节目中发生的事情。参赛者会从三道帘子中选择一道。一道帘子里装着非常珍贵的奖品,另外两道帘子里装着小奖品。为了便于讨论,我们假设一道帘子后面是一辆汽车,另外两道帘子后面是一只山羊。那么蒙蒂总是会,我再说一遍,总是会,打开两道未被选中的帘子中的一道,露出一只山羊。经过数百场节目的检验,这意味着蒙蒂·霍尔(主持人)知道汽车的位置,并故意打开一道露出山羊的帘子。显然,当参赛者选择自己的帘子时,它露出汽车的概率是1/3,而两道未被选中的帘子中一道露出汽车的概率是2/3。因此,蒙蒂注定会打开一道未被选中、包含目标的帘子。“注定”是这里的关键词。因为蒙蒂在这个阶段无法打开参赛者的帘子,所以参赛者的帘子露出汽车的概率仍然保持在1/3。未选择的窗帘露出汽车的概率仍然是2/3,但现在汽车都出现在一个窗帘上了。因此,当一只山羊被揭开后,玩家的窗帘上有汽车的概率是1/3,而另一个未打开的窗帘上有汽车的概率是2/3,因此换窗帘是一个明智的选择。
下表列出了所有可能的结果。在玩家选择汽车窗帘的情况下,我让蒙蒂随意拉开一个窗帘。可以看到,不拉开窗帘的获胜概率为 1/3,而拉开窗帘的获胜概率为 2/3。
我们做个交易吧
| 玩家 选择 | 车 | 窗帘 已打开 | 可能性 | 获胜者 交换 |
| 1 | 1 | 1 | 0% | 无 |
| 1 | 1 | 2 | 5.56% | 否 |
| 1 | 1 | 3 | 5.56% | 否 |
| 1 | 2 | 1 | 0% | 无 |
| 1 | 2 | 2 | 0% | 无 |
| 1 | 2 | 3 | 11.11% | 是 |
| 1 | 3 | 1 | 0% | 无 |
| 1 | 3 | 2 | 11.11% | 是 |
| 1 | 3 | 3 | 0% | 无 |
| 2 | 1 | 1 | 0% | 无 |
| 2 | 1 | 2 | 0% | 无 |
| 2 | 1 | 3 | 11.11% | 是 |
| 2 | 2 | 1 | 5.56% | 否 |
| 2 | 2 | 2 | 0% | 无 |
| 2 | 2 | 3 | 5.56% | 否 |
| 2 | 3 | 1 | 11.11% | 是 |
| 2 | 3 | 2 | 0% | 无 |
| 2 | 3 | 3 | 0% | 无 |
| 3 | 1 | 1 | 0% | 无 |
| 3 | 1 | 2 | 11.11% | 是 |
| 3 | 1 | 3 | 0% | 无 |
| 3 | 2 | 1 | 11.11% | 是 |
| 3 | 2 | 2 | 0% | 无 |
| 3 | 2 | 3 | 0% | 无 |
| 3 | 3 | 1 | 5.56% | 否 |
| 3 | 3 | 2 | 5.56% | 否 |
| 3 | 3 | 3 | 0% | 无 |
与此同时,在“一掷千金”游戏中,一切都没有注定。假设游戏中剩余的金额分别为 0.01 美元、1 美元和 100 万美元。如果剩下三个箱子,那么打开的箱子里有可能包含一百万美元。下表显示了剩下三个箱子的可能结果。记住,玩家不能打开自己的箱子。
成交或不成交
| 玩家 选择 | 百万美元 | 案件 已打开 | 可能性 | 获胜者 交换 |
| 1 | 1 | 1 | 0% | 无 |
| 1 | 1 | 2 | 5.56% | 否 |
| 1 | 1 | 3 | 5.56% | 否 |
| 1 | 2 | 1 | 0% | 无 |
| 1 | 2 | 2 | 5.56% | 绝望 |
| 1 | 2 | 3 | 5.56% | 是 |
| 1 | 3 | 1 | 0% | 无 |
| 1 | 3 | 2 | 5.56% | 是 |
| 1 | 3 | 3 | 5.56% | 绝望 |
| 2 | 1 | 1 | 5.56% | 绝望 |
| 2 | 1 | 2 | 0% | 无 |
| 2 | 1 | 3 | 5.56% | 是 |
| 2 | 2 | 1 | 5.56% | 否 |
| 2 | 2 | 2 | 0% | 无 |
| 2 | 2 | 3 | 5.56% | 否 |
| 2 | 3 | 1 | 5.56% | 是 |
| 2 | 3 | 2 | 0% | 无 |
| 2 | 3 | 3 | 5.56% | 绝望 |
| 3 | 1 | 1 | 5.56% | 绝望 |
| 3 | 1 | 2 | 5.56% | 是 |
| 3 | 1 | 3 | 0% | 无 |
| 3 | 2 | 1 | 5.56% | 是 |
| 3 | 2 | 2 | 5.56% | 绝望 |
| 3 | 2 | 3 | 0% | 无 |
| 3 | 3 | 1 | 5.56% | 否 |
| 3 | 3 | 2 | 5.56% | 否 |
| 3 | 3 | 3 | 0% | 无 |
“一掷千金”表格显示,如果剩下三个箱子,玩家打开百万美元箱子的概率是1/3(无望中奖),换人获胜的概率是1/3,换人输的概率也是1/3。因此,换人箱子的概率相同。如果只剩下两个箱子,那么每个箱子中大奖的概率就是50/50。
又到了“一掷千金”的问题了。假设银行家和席琳·迪翁客串演出之后,你只剩下两个箱子,50万美元和100万美元。我猜银行家的出价会略低于75万美元。你会选哪个?如果剩下的两个箱子分别是0.01美元和100万美元呢?我想这完全取决于你是不是赌徒,和赔率没关系。我问这个问题的原因是,我想知道是否有人能赢得100万美元(即使他们选的是那个神奇的箱子)。
当奖金数额足以改变人生时,明智的玩家应该谨慎行事,而非最大化预期价值。一个好的策略应该是最大化预期幸福感。我认为衡量幸福感的一个好函数是你总财富的对数。假设一个人现有财富为 10 万美元,面临 0.01 美元和 100 万美元两种情况。选择“不交易”的预期幸福感为 0.5*log(100,000.01 美元) + 0.5*log(1100,000 美元) = 5.520696。设 b 表示玩家无所谓是否接受的银行报价。
对数(b)= 5.520696
b = 10 5.520696
b = 331,662.50 美元。
所以这位假设的玩家应该对银行出价 331,662.50 美元无动于衷。你投入的资金越少,就越应该谨慎行事。通常在游戏后期,银行出价接近预期价值,有时甚至会略高一些。玩家赢得百万美元的唯一合理情况是,他投入了大量资金,并且/或者银行出价异常低廉。制作人似乎喜欢勤劳的中产阶级,所以我们不太可能看到有人在涉及大额资金时如此傲慢。我也从未见过银行在游戏后期出价低于预期价值 90% 的金额。我们只有在某个无法停止赌博的堕落赌徒出现时才会看到有人赢得百万美元。当这种情况发生时,我会支持银行家。
这是《一掷千金》(Deal or No Deal)的后续报道,我最近才第一次看。你的分析假设庄家不知道箱子里钱的价值。然而,在我看的节目中,在最后阶段,两位选手都选择了一个有价值的箱子,并且都获得了(或者说,由于其中一位已经退出,他们本应获得)高于预期价值(EV)的赔付。在最极端的情况下,当玩家剩下的两个金额分别为50万美元和75万美元时,他们“本应”获得68.7万美元的赔付。对此唯一合理的解释是,庄家知道玩家箱子的价值,并且提供的赔付是基于此的。
这只是我的一点看法,无需回复。
谢谢你没有期待我的回复,但我通常都会回答游戏节目的问题。节目中每一集都声称盒子里的金额是随机的,Howie 和银行家都不知道结果。这在《让我们做个交易》中从未被提及,但蒙提·霍尔显然知道结果。我也见过银行家给出高于预期的最后报价,尤其是金额较大的时候。我坚信,这并不是因为银行家知道玩家盒子里有什么。20 世纪 50 年代, 《21》等节目被曝出存在操纵,引发了一场巨大的丑闻。没有任何令人信服的理由为了通过银行报价攫取一些奖金而毁掉一档成功的节目和所有游戏节目的完整性。
我可以提出三种理论来解释为什么银行家有时提供的金额高于其余案例的平均金额。
- 这部剧试图将银行家描绘成在办公室里为钱操心的人物。豪伊·曼德尔经常评论银行家的情绪和语气。或许,将银行家描绘成一个规避风险的精打细算者,宁愿止损也不愿冒险发放巨额奖金,会让这部剧更具戏剧性。
- 真正的银行家确实厌恶风险。这有点超出我的专业范围了,但据我所知,游戏和真人秀通常由独立于电视网络的公司制作。这些规模较小的公司会寻求保险公司的帮助,以降低参赛者赢得巨额奖金的风险。在这种情况下,保险公司才是真正的银行家,并且可能会影响节目中银行家的行为。承保此类稀奇古怪事件的保险公司规模并不大,在涉及大额金额时可能更倾向于稳妥行事。
在您的例子中,银行家的报价比预期价值高出9.92%。如果银行家遵循凯利准则,那么在总资金只有782,008美元的情况下,这样的报价也不足为奇,这低于最高奖金。任何一家有自尊心的保险公司都不会如此保守。显然,仅凭这一点不足以证明您例子中的报价是合理的。
- 节目试图让参赛者看起来愚蠢又贪婪。像《你比五年级学生聪明吗?》和《今夜秀》的“乱穿马路”这样的节目,如果我们不能从嘲笑那些被琐事难倒的人中找到一些满足感,那它们就不可能成功。 《朋友还是敌人》和《最弱环节》这两档节目则出色地揭露了人性的贪婪。我必须承认,当参赛者拒绝高于预期的报价,最终接受较低金额时,我感到幸灾乐祸。
我倾向于认为原因是这三个原因的综合,但主要是第三个原因。
如果我的回答到此结束,肯定会有人评论,质疑银行家们是否真的会提出这些假设性报价。言下之意是,这些报价是为了达到戏剧效果而夸大其词。我记录了13场比赛的具体情况。其中一场比赛,还剩三个案子(1000美元、5000美元和50000美元),平均价格为18667美元,而最终报价为21000美元,比预期价格高出12.5%。另一场比赛,还剩两个案子(400美元和750000美元),平均价格为375200美元,最终报价为400000美元,比预期价格高出6.6%。所以,我认为没有理由质疑这些假设性报价的可靠性。
链接:
一掷千金公式:本页面展示了基于一掷千金网站上的免费游戏的用于计算银行家报价的新旧公式。
在《最后的危险边缘》中,如果分数如下,站在每个人的角度,你会下多少钱:
玩家A:10,000美元
玩家B:8,000美元
玩家C:3,500美元
首先,我先做一些假设。首先,我假设这三位选手对《最终危险边缘》中的投注行为一无所知,除了表格中给出的正确概率。其次,我假设了解类别没有任何帮助。第三,我还假设三位选手都想争取胜利,不想让另一位选手打成平手。
让我们从玩家C开始。他应该预期,如果B猜对了,A可能会下注6001美元,以保持领先于B。然而,如果A猜错了,他的筹码就会降到3999美元。在这种情况下,C需要至少下注500美元,并且猜对了,才能击败A。然而,在我看来,如果必须猜对才能赢,那不妨下大注。所以,如果我是CI,我会孤注一掷。
B 左右为难,不知道该押大还是押小。小额投注应该不超过 999 美元,这样才能在 C 正确的情况下保持高于 C 的赔率。小额投注的好处是,无论怎样,都能保持在 C 之上,希望 A 押大,但结果却是错的。大额投注不一定要押全,但也有可能。大额投注的好处是,希望 A 押小,或者押大但结果却是错的,但两者都需要 B 正确。
A 基本上想和 B 走同一条路。A 的小额投注可以是 0 美元到 1000 美元之间的任何金额,如果 B 下注 999 美元,A 的投注额就会高于 B 的投注额。大额投注应该是 6001 美元,这样既能保证 A 猜对了就能赢,又能在 B 下大注,而其他三位玩家都猜错的情况下保住胜算。
为了帮助计算正确和错误答案的八种可能结果的概率,我查看了 j-archive.com(现已停用)上第 20 季至第 24 季的《危险边缘》最终结果。结果如下:玩家 A 领先,其次是玩家 B,C 垫底。
《最终危险》的可能结果
| 玩家A | 玩家B | 玩家C | 可能性 |
| 正确的 | 正确的 | 正确的 | 21.09% |
| 正确的 | 正确的 | 错误的 | 9.73% |
| 正确的 | 错误的 | 正确的 | 10.27% |
| 错误的 | 正确的 | 正确的 | 8.74% |
| 正确的 | 错误的 | 错误的 | 13.33% |
| 错误的 | 正确的 | 错误的 | 10.27% |
| 错误的 | 错误的 | 正确的 | 8.63% |
| 错误的 | 错误的 | 错误的 | 17.92% |
使用我在我的网站mathproblems.info上的问题 192 中解释的博弈论逻辑,我发现 A 和 B 应该按如下方式随机化他们的策略。
玩家 A 应该下大注的概率为 73.6%,下小注的概率为 26.4%。
玩家 B 应该以 67.3% 的概率下大注,以 32.7% 的概率下小注。
玩家 C 应该以 100.0% 的概率下大赌注。
如果遵循这一策略,每个玩家获胜的概率如下:
玩家A:66.48%
玩家B:27.27%
玩家C:6.25%
顺便说一句,根据上表,领先者答对《最终危险边缘》的概率为 54.4%,第二名玩家为 49.8%,第三名玩家为 48.7%。总体概率为 51.0%。
从实际操作上讲,玩家确实了解投注行为。在我看来,玩家下注的次数往往超出了数学上的合理范围。有趣的是,我发现在“每日双倍”节目中投注过于保守,超出了数学上的合理范围。我认为肯·詹宁斯之所以表现如此出色,原因之一就是他在“双倍双倍”节目中下注激进。总之,如果我真的上节目,我会假设其他两位玩家也会下注激进。所以我实际的投注金额是:A 下注 6000 美元(对 B 友善),B 下注 0 美元,C 下注 3495 美元(留一点未下注金额,以防 A 愚蠢地押上所有金额或只剩 1 美元,结果错了)。
在有人向我提问如何在实际场地中抽取随机数之前,让我先建议一下斯坦福·黄 (Stanford Wong) 的策略,即使用手表的秒针从 1 到 60 中抽取一个随机数。
一档名为“金钱本色”的全新游戏节目在英国首播。节目中,一位参赛选手随机获得一笔目标金额,据悉该金额在5.5万英镑到7.9万英镑之间。为了赢钱,参赛选手需要从20台自动取款机中选择10台,每台机器的存款额从1000英镑到20000英镑不等,以1000英镑为增量递增。当他选择一台机器时,机器会从1000英镑开始递增,以1000英镑为增量递增。
玩家可以随时喊“停!”,然后他会将屏幕上显示的金额存入账户。如果玩家没有及时停止,导致机器的钱用完,则他不会存入任何金额。服务员会提供统计数据,例如剩余的机器数量、剩余的赢钱金额、每台机器的平均赢钱金额以及机器中剩余的金额。
玩家可以“玩空档”,也就是说,如果连续选中的机器分别为 4000 英镑、5000 英镑和 6000 英镑,那么一旦其中一台机器的投注额超过 3000 英镑,就保证能达到 7000 英镑。我的问题是,玩家应该使用什么样的策略?
这种事我得花上几周时间分析。可惜的是,我几乎在三个月后才看到你的留言,因为当时积压了大量“问问巫师”的问题。维基百科页面似乎显示那部剧很失败,已经被取消了。不过,这仍然引出了一个有趣的问题。
女服务员会很贴心地告诉你每台剩余机器达到目标所需的平均金额。经过几个小时的反复思考,我实在想不出比设定的平均值高出约 25% 的停止目标更好的办法了。这只是一个有根据的猜测,所以请不要让我证明它是最优的。正如你所说,也要抓住机会,不要在已经选好的金额之前停下来。
当只剩下两台机器时,如果所需金额不超过13,000英镑,我会尽量在倒数第二台机器上全部买入。如果所需金额超过14,000英镑,我会尽量在下一台机器上买一半。
如果他们真的要重启这部剧,我希望我的英国读者能告诉我。这类谜题可能会让我着迷,就像《永恒谜题》一样,巧合的是(或许也巧合)它也在英国上映了。
附言:为什么在英国,“colour”要用au拼写?我不明白。
《The Price is Right》中的 Punch a Bunch 游戏每次出拳的平均奖金和最佳策略是多少?
对于那些不熟悉规则的人,可以在“价格猜猜猜”网站上查看规则说明。如果您不熟悉这个游戏,请花点时间去那里看看,因为我假设您知道规则。YouTube上也有一些关于这个游戏的视频。这里有一个旧视频,展示了第二次机会,但当时的最高奖金只有1万美元。现在是2.5万美元。
首先,我们来计算一下没有第二次机会的奖金的预期价值。下表显示,平均为1371.74美元。
打出一堆奖品,没有第二次机会
| 奖 | 数字 | 可能性 | 预期胜利 |
| 25000 | 1 | 0.021739 | 543.478261 |
| 10000 | 1 | 0.021739 | 217.391304 |
| 5000 | 3 | 0.065217 | 326.086957 |
| 1000 | 5 | 0.108696 | 108.695652 |
| 500 | 9 | 0.195652 | 97.826087 |
| 250 | 9 | 0.195652 | 48.913043 |
| 100 | 9 | 0.195652 | 19.565217 |
| 50 | 9 | 0.195652 | 9.782609 |
| 全部的 | 46 | 1.000000 | 1371.739130 |
其次,计算有第二次机会的平均奖金。下表显示,平均奖金为225美元。
利用第二次机会赢得丰厚奖金
| 奖 | 数字 | 可能性 | 预期胜利 |
| 500 | 1 | 0.250000 | 125.000000 |
| 250 | 1 | 0.250000 | 62.500000 |
| 100 | 1 | 0.250000 | 25.000000 |
| 50 | 1 | 0.250000 | 12.500000 |
| 全部的 | 4 | 1.000000 | 225.000000 |
第三,根据玩家找到的第二次机会数量创建一个预期价值表。这可以通过简单的数学计算得出。例如,2次第二次机会的概率为(4/50)×(3/49)×(46/48)。s次机会的预期收益为1371.74美元+s×225美元。下表显示了0到4次第二次机会的概率和平均收益。
Punch a Bunch 奖品返还表
| 第二次机会 | 可能性 | 平均胜利 | 预期胜利 |
| 4 | 0.000004 | 2271.739130 | 0.009864 |
| 3 | 0.000200 | 2046.739130 | 0.408815 |
| 2 | 0.004694 | 1821.739130 | 8.551020 |
| 1 | 0.075102 | 1596.739130 | 119.918367 |
| 0 | 0.920000 | 1371.739130 | 1262.000000 |
| 全部的 | 1.000000 | 1390.888067 |
因此,每次出拳的平均赢利(包括第二次机会的额外奖金)为 1390.89 美元。
下表展示了我根据剩余击球次数确定最低赢额的策略。请注意,玩家可以通过三次第二次机会赢得 1,000 美元 + 250 美元 + 100 美元 + 50 美元的奖金,最终赢得 1,400 美元。
打击一堆策略
| 剩余冲孔数 | 最低站立高度 |
| 3 | 5,000 美元 |
| 2 | 5,000 美元 |
| 1 | 1,400美元 |
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
如果您不确定答案,那么在游戏节目《百万美元大洒千里》中分配资金的最佳策略是什么?
为了其他读者的利益,让我先回顾一下规则。
- 一支球队的起步资金为 1,000,000 美元。
- 团队需要回答一道选择题。
- 团队要把钱分给所有可能的答案。所有投在正确答案上的钱都会进入下一个问题。
- 团队必须完全排除至少一个可能的答案,不投入任何资金。
- 这个过程重复几轮。玩家也有一次改变主意的机会。
显然,如果团队确定答案,那么他应该把所有钱都押在正确答案上。如果团队能把答案缩小到两个,但每个答案都有50%的正确概率,那么他们应该把钱平均分配给这两个选项。
如果团队倾向于某个答案,但又不完全排除其他一个或多个答案,情况就会变得更加困难。我们来看一个例子。假设团队确定每个正确答案的概率如下:A 10%,B 20%,C 30%,D 40%。他们应该如何分配他的钱?
我认为答案是遵循凯利准则。简而言之,团队应该在每次提问时最大化其财富对数。要做到这一点,你必须考虑你已经拥有多少财富。
假设您现有的财富(独立于节目本身积累)为 100,000 美元。这是您的第一个问题,因此您需要分配 1,000,000 美元的游戏节目奖金。首先,排除概率最低的选项,以符合节目规则。然后,您需要最大化 0.2×log(100,000+b*1,000,000) + 0.3×log(100,000+c*1,000,000) + 0.4×log(100,000+d*1,000,000),其中小写的 a、b 和 c 分别代表每个答案的分配比例。
这可以用微积分和解三项式方程、反复试验,或者我更喜欢用Excel的“目标搜索”功能来解答。无论你用什么方法,正确答案都是B占18.9%,C占33.3%,D占47.8%。
当然,节目里没人能在规定时间内完成所有这些数学题,更别提你还得在这段时间内转移一大堆现金。我更实际的建议是,根据你对答案正确概率的评估来分配资金,假设最不可能的选项不存在。在这个例子中,B选项分配22.2%,C选项分配33.3%,D选项分配44.4%。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
密歇根州彩票有一款三人游戏,规则如下: 在这场游戏中,最后出局有什么位置优势吗?每位玩家的最佳策略是什么? 这里有一个YouTube视频,展示了这场游戏。
首先,最后行动没有任何位置优势。由于在前面的玩家进行游戏时,玩家会被安排在隔音室内,所以顺序并不重要。
其次,博弈中必须存在一个纳什均衡,其中至少获得 x 分的策略优于其他任何策略。问题在于找到 x。
我问自己,如果每位玩家拿到的不是1到100的牌,而是0到1之间均匀分布的随机数,并寻找一个点x,让完美的逻辑学家对停牌和换牌无感,那么策略会是什么。有了这个答案,我们就能很容易地将答案应用到1到100的离散分布中。
我就不多说了,让读者自己体会这个问题的乐趣吧。查看下面的链接获取答案和解决方案。
答案为从 0 到 1 的连续分布。
答案为 1 到 100 的离散分布。
如需了解我的解决方案,请点击此处(PDF) 。
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
假设不知道任何东西的价格,那么《价格猜猜猜》中的竞赛游戏的最佳策略是什么?
对于不熟悉规则的玩家,玩家会得到四个价格标签,必须将它们贴在四件物品上。完成后,玩家拉动一个拉杆,拉杆会显示正确匹配的数量。如果玩家的正确匹配次数少于四个,则可以重新排列标签,然后重试。玩家可以在45秒内尝试尽可能多的次数。
我的建议是,根据之前的选择和得分历史,始终提交有获胜机会的选择。如果第一个得分为 0,则不要将两组标签颠倒过来,而是将所有内容向任意方向移动一位。
如果你无法当场理解逻辑,下面我会为你详细说明。要使用此策略,请为不同的标签分配字母 A、B、C 和 D。然后按照图示顺序,从左到右将它们放置在舞台上。始终从 ABCD 开始。然后,查看下面的乐谱历史记录,并选择与该乐谱序列对应的标签顺序。
如果为 0,则 BCDA
如果 0-0,则 CDAB
如果 0-0-0,则 DABC(必须赢)
如果是 0-1,则为 BDAC
如果 0-1-0,则 CADB(必须赢)
如果 0-1-1,则 CDBA
如果 0-1-1-0,则 DCAB(必须赢)
如果 0-2,则 BADC
如果 0-2-0,则 DCBA(必须赢)
如果为 1,则 ACDB
如果 1-0,则 BDCA
如果 1-0-0,则 CABD
如果 1-0-0-1,则 CBAC(必须获胜)
如果 1-1,则 BDCA
如果 1-1-0,则 CABD
如果 1-1-0-1,则 CBAC(必须获胜)
如果 1-1-1,则 BCAD(必胜)
如果是 2,那么 ABDC
如果 2-0,则 BACD(必须赢)
如果 2-1,则 ACBD
如果是 2-1-0,则 DBCA
如果 2-1-1,则 ADCB
如果 2-1-1-0,则 CBAD(必须赢)
下表显示了每个总圈数的概率。右下角单元格显示预期圈数为 10/3。
赛车游戏
| 转弯 | 组合 | 可能性 | 返回 |
|---|---|---|---|
| 1 | 1 | 0.041667 | 0.041667 |
| 2 | 4 | 0.166667 | 0.333333 |
| 3 | 8 | 0.333333 | 1.000000 |
| 4 | 8 | 0.333333 | 1.333333 |
| 5 | 3 | 0.125000 | 0.625000 |
| 全部的 | 24 | 1.000000 | 3.333333 |
我在Wizard of Vegas论坛上讨论过这个问题。
在“价格猜猜猜”节目的 Showcase Showdown 中,任何特定玩家赢得 25,000 美元的概率是多少?
为了向其他读者解释一下,让我先解释一下你在说什么。Showcase Showdown 是游戏节目《价格猜猜猜》中的一款游戏。在 Showcase Showdown 中,每个玩家轮流旋转一个轮盘,该轮盘停在从 0.05 到 1.00 的每个能被 0.05 整除的数额上的概率相等。如果玩家对第一次旋转不满意,他们可以再次旋转,将第二次旋转加到第一次旋转上,但是如果超过 1.00,他们将立即被取消资格。如果出现平局,每个玩家将在决胜局中获得一次旋转机会,最高旋转次数获胜。如果再次出现平局,此过程将重复,直到打破平局。
展示赛对决的主要目的是晋级展示赛。不过,参赛者也可以获得现金奖励,具体如下:
- 在第一轮中,如果任何玩家获得总计 1.00 美元,无论是一次总和还是两次旋转的总和,他都将赢得 1,000 美元。
- 在第一轮(也是唯一一轮)决胜局中,如果轮盘停在 0.05 美元或 0.15 美元,则玩家将赢得 10,000 美元。
- 在第一轮(也是唯一一轮)决胜局中,如果轮盘上出现 1.00 美元,那么玩家将赢得 25,000 美元。
我在第101栏解释了Showcase Showdown的最佳策略。假设遵循该策略,下表将解答您的疑问以及其他各种问题。
展示摊牌统计
| 问题 | 回答 |
|---|---|
| 预计首轮奖金 1000 美元的赢家 | 0.253790 |
| 两人打平的概率 | 0.113854 |
| 三人平局概率 | 0.004787 |
| 预计第二轮奖金 10,000 美元的获胜者 | 0.024207 |
| 预计第二轮奖金 25,000 美元 | 0.012104 |
| 预计总奖金 | 798.45 美元 |
| 任何特定玩家赢得 1000 美元的概率 | 0.084597 |
| 任何特定玩家赢得 10,000 美元的概率 | 0.008069 |
| 任何特定玩家赢得 25,000 美元的概率 | 0.004035 |
表格的底行显示,如果您进行 Showcase Showdown,不考虑您的旋转顺序,您赢得 25,000 美元的机会是 0.004035,即 248 分之一。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
在游戏节目《幸存者》中,有两支队伍,一支有九名队员,另一支有六名队员。之后,他们被随机分成三支新的队伍,每支队伍五人。每支新队伍由原九人队伍中的三名成员和原六人队伍中的两名成员组成。这种情况发生的概率是多少?
我们将之前的九人队称为队1,将六人队称为队2。从队1中挑选三名球员,从队2中挑选两名球员的方式数为combin(9,3) × combin(6,2) = 1,260。从15名球员中挑选五名球员的方式总数为combin(15,5) = 3,003。因此,第一队被分成3/2,有利于队1的概率为1,260/3,003 = 41.96%。
如果发生这种情况,那么球队 1 将剩下 6 名球员,球队 2 将剩下 4 名球员。从球队 1 中挑选 3 名球员,从球队 2 中挑选 2 名球员的方式数为 combin(6,3)×combin(4,2) = 120。从剩下的 10 名球员中挑选 5 名球员的方式总数为 combin(10,5) = 252。因此,假设球队 1 已经按照 3/2 的分配方案分配,那么球队 2 被 3/2 分配的概率为 120/252 = 47.62%。
如果前两支新队伍的分成比例为 3/2,有利于前一支队伍 1,那么最终的队伍将在剩余队伍中以 3/2 的比例分配。
因此,您问题的答案是 41.96% × 47.62% × 100% = 19.98%。
公式:
组合(x,y)=x!/((y!*(xy)!)
x!= 1*2*3*...*x
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
我认为詹姆斯·霍尔扎伊尔在他上一场比赛中故意输给艾玛。我的证据是,在那之前他每场比赛都押大注,但突然在对阵艾玛的比赛中押小注。我怀疑制作人想让肯·詹宁斯在亚历克斯下台后主持节目。如果主持人拥有两场节目的记录,并且赢了钱,节目会更有戏剧性。所以,他们花钱雇了詹姆斯来打假球。
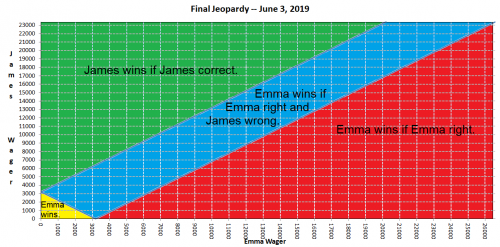
让我先介绍一下背景。2019年6月3日,詹姆斯距离打破常规比赛总奖金纪录仅一步之遥,目前该纪录仍为2,520,700美元。詹姆斯的场均赢利远超打破纪录所需的金额。因此,6月3日,所有人的目光都聚焦在这项纪录被打破上。
而结果却是,詹姆斯不仅没能打破纪录,还输了。冠军艾玛不仅策略性十足,而且反应灵敏,回答问题也非常准确。她的表现和詹姆斯一如既往。进入《危险边缘》决赛时,得分如下:
- 艾玛——26,600美元
- 詹姆斯——23,400美元
- 杰伊——11,000美元
在这种情况下,第二名的奖金超过第一名的一半,而第三名的奖金却不足一半,通常就取决于第一名和第二名最终的投注金额是高还是低。如果投注金额高,第一名的奖金就足以锁定胜局。具体来说,投注金额是第二名得分的两倍减去第一名得分加上一美元。这正是艾玛投注金额的方式,投注金额为 2×23,400 美元 - 26,600 美元 + 1 美元 = 20,201 美元。大多数情况下,第一名的玩家都会这样做。
然而,詹姆斯在决定赌注时并不知道艾玛会怎么做。下表显示了根据哪种赌注组合,谁将获胜。
如果艾玛下注至少 20,201 美元,那么如果正确的话,她将锁定胜利。
如果 Emma 下注较低,那么如果 (a) James 下注较低或 (b) James 下注较高但错误,她将获胜。
如果詹姆斯下注高,那么如果 (a) 艾玛下注高,艾玛错了,詹姆斯是对的,或者 (b) 艾玛下注低,詹姆斯是对的,那么他就赢了。
如果詹姆斯下注低,而艾玛下注高并且错了,那么他就赢了。
如果玩的是完美逻辑学家,两人都会随机做出决定。然而,在这种容易被抓住的情况下,领导者很少会选择低牌。如果詹姆斯预料到艾玛会走高牌,那他绝对应该走低牌。这样,他不用在《危险边缘》中完全正确就能赢,只需要祈祷艾玛搞砸了就行了。
如果杰伊全押并且猜对了,那么詹姆斯的实际出价就是可以覆盖杰伊的正确金额:23,400 美元 - 2×11,000 美元 - 1 美元 = 1,399 美元,这对于击败艾玛来说是一个低赌注。
如果猜对了,詹姆斯将因获得第二名而比获得第三名多获得 1,000 美元。
总而言之,我完全否认詹姆斯输掉比赛的阴谋论。他打球的方式是正确的,但输球的原因既有强大的对手,也有大多数人所说的“运气不好”。
外部链接
- 《危险边缘》名人堂
- James Holzhauer 谈论《危险边缘》 ——我在《拉斯维加斯巫师》论坛上的讨论。
在《危险边缘》的“最终挑战”中,如果第二名玩家的奖金比第一名玩家多出三分之二,那么最佳策略是什么?假设第三名玩家不参与游戏。
首先声明一下。以下分析基于统计平均值。实际玩家应该根据自己对“最终危险”类别的了解程度以及对手答对的概率进行心理调整。
为了回答你的问题,我首先查看了《危险边缘》档案库中的四个季度的数据,以了解第一名(领先者)和第二名(追赶者)玩家在《危险边缘》决赛中正确和错误表现的四种可能组合。
最终《危险边缘》记分卡
| 领先球员 | 追逐球员正确 | 追逐球员不正确 | 全部的 |
|---|---|---|---|
| 正确的 | 29.0% | 25.5% | 54.5% |
| 不正确 | 17.7% | 27.8% | 45.5% |
| 全部的 | 46.8% | 53.2% | 100.0% |
在继续之前,让我们定义一些变量:
x = 领先球员得分较高的概率。
y = 追逐球员走高的概率。
f(x,y) = 高玩家获胜的概率。
让我们用上表中的 x 和 y 来表示 f(x,y):
f(x,y) = 0.823xy + 0.545x(1-y) + 0.468(1-x)y + (1-x)(1-y)
f(x,y) = 0.810 xy - 0.455x - 0.532y + 1
为了找到 x 和 y 的最佳值,让我们对 x 和 y 取 f(x,y) 的导数。
f(x,y) d/dx = -0.455 + 0.810y = 0
因此 y = 0.455/0.810 = 0.562
f(x,y) d/dy = -0.532 + 0.810x = 0
因此 x = 0.523/0.810 = 0.657
因此,高玩家下高注的概率为 65.7%,低玩家下高注的概率为 56.2%。
根据观察,我认为高玩家下注高额的概率超过 65.7%,因此如果我排在第二位,我会下低额赌注。
如果两个玩家都遵循这种随机策略,那么领先玩家获胜的概率为 70.1%。
抛开所有理论不谈,如果你领先,预测追赶者会做什么,然后照做。如果你追赶,预测领先者会做什么,然后反其道而行之。此策略适用于所有此类锦标赛。这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
在《危险边缘》一轮开始时,为什么有些玩家,比如詹姆斯·霍尔茨豪尔,会从最底层开始选?先从最上面的简单问题热身不是更合理吗?部分原因是为了确保玩家对这个类别有充分的理解,因为这些类别有时比较棘手。
原因是每日双倍奖励有91.5%的概率被放置在最底下的三行。下表显示了在13,660个每日双倍奖励中,它们在面板上的位置。
每日双人间位置
| 排 | 第 1 列 | 第 2 列 | 第 3 列 | 第 4 列 | 第 5 列 | 第 6 栏 | |
|---|---|---|---|---|---|---|---|
| 1 | 5 | - | 3 | 3 | 2 | 3 | 16 |
| 2 | 280 | 137 | 216 | 167 | 207 | 140 | 1,147 |
| 3 | 820 | 442 | 677 | 658 | 643 | 472 | 3,712 |
| 4 | 1,095 | 659 | 982 | 907 | 895 | 627 | 5,165 |
| 5 | 787 | 403 | 670 | 671 | 613 | 476 | 3,620 |
| 全部的 | 2,987 | 1,641 | 2,548 | 2,406 | 2,360 | 1,718 | 13,660 |
资料来源: J! 档案。
这是以每日双倍在棋盘的每个单元格中出现的频率的形式呈现的相同数据。
每日双倍概率
| 排 | 第 1 列 | 第 2 列 | 第 3 列 | 第 4 列 | 第 5 列 | 第 6 栏 | |
|---|---|---|---|---|---|---|---|
| 1 | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.1% |
| 2 | 2.0% | 1.0% | 1.6% | 1.2% | 1.5% | 1.0% | 8.4% |
| 3 | 6.0% | 3.2% | 5.0% | 4.8% | 4.7% | 3.5% | 27.2% |
| 4 | 8.0% | 4.8% | 7.2% | 6.6% | 6.6% | 4.6% | 37.8% |
| 5 | 5.8% | 3.0% | 4.9% | 4.9% | 4.5% | 3.5% | 26.5% |
| 全部的 | 21.9% | 12.0% | 18.7% | 17.6% | 17.3% | 12.6% | 100.0% |
寻找每日双倍奖励的原因是,这是让你的分数翻倍的好方法。大多数参赛者对任何给定线索的正确率都在 80% 到 90% 左右。如果能押注 80% 到 90% 的胜率,那么赢得等额的奖金就非常划算了。詹姆斯·霍尔茨豪尔之所以能赢得这么多奖金,一个主要原因就是他积极地寻找每日双倍奖励,而且一旦找到,大多数时候都会“全押”。这也是他输给艾玛的原因,当时艾玛也用同样的策略对付他。
假设玩家不知道奖品的价格,那么在“价格猜猜猜”游戏中玩竞赛游戏的最佳策略是什么?
为了让不熟悉该游戏的读者了解一下,这里有一个该游戏的视频。
我认为以下策略的平均回合数最低。有很多策略可以与之匹敌,但我认为没有哪个策略能超越它。
要使用该策略,请将四个价格标签标记为 1、2、3 和 4。根据您过去正确回答的问题的历史记录,从左侧的第一个转弯开始,将它们放在四个奖品上。
竞赛游戏策略
| 历史 | 一等奖 | 奖品二 | 三等奖 | 奖品 4 |
|---|---|---|---|---|
| 没有任何 | 1 | 2 | 3 | 4 |
| 0 | 2 | 1 | 4 | 3 |
| 0,0 | 3 | 4 | 2 | 1 |
| 0,0,0 | 4 | 3 | 1 | 2 |
| 0,0,2 | 3 | 4 | 1 | 2 |
| 0,0,2,0 | 4 | 3 | 2 | 1 |
| 0.2 | 2 | 3 | 4 | 1 |
| 0,2,0 | 4 | 1 | 2 | 3 |
| 0,2,1 | 2 | 4 | 1 | 3 |
| 0,2,1,0 | 3 | 1 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 1,0 | 2 | 4 | 3 | 1 |
| 1,0,0 | 3 | 1 | 2 | 4 |
| 1,0,0,0 | 4 | 2 | 1 | 3 |
| 1,1 | 1 | 4 | 2 | 3 |
| 1,1,0 | 2 | 3 | 1 | 4 |
| 1,1,0,0 | 3 | 2 | 4 | 1 |
| 1,1,0,0,0 | 4 | 1 | 3 | 2 |
| 2 | 2 | 1 | 3 | 4 |
| 2,0 | 1 | 2 | 4 | 3 |
| 2,1 | 1 | 3 | 2 | 4 |
| 2,1,0 | 4 | 2 | 3 | 1 |
| 2,1,1 | 1 | 4 | 3 | 2 |
| 2,1,1,0 | 3 | 2 | 1 | 4 |
下表显示了在 24 种可能的排列方式中,四个价格标签需要 1 到 5 次旋转的概率。
所需圈数
| 转弯 | 数字 | 可能性 |
|---|---|---|
| 1 | 1 | 4.17% |
| 2 | 4 | 16.67% |
| 3 | 8 | 33.33% |
| 4 | 9 | 37.50% |
| 5 | 2 | 8.33% |
| 全部的 | 24 | 100.00% |
取点积,该策略下所需的平均转数为 3.29167。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
我听说了《危险边缘》的投注规则,叫“三分之二规则”。你知道吗?
是的。这指的是当第二名玩家的得分超过第一名玩家的2/3时,他的策略会发生变化。
让我们将情况简化为双人游戏,如下所示:
- 情况A:第二名的人数还不到第一名的一半。
- 情况 B:第二个玩家拥有第一名的 1/2 到 2/3 份额。
- 情况C:第二名拥有第一名的2/3以上。
在继续深入讨论之前,我想提醒读者一下《危险边缘》规则的一项变化,该规则在“最终危险边缘”之后对平局进行了修改。现在不再是双方选手同时晋级,而是设置一个突然死亡决胜题。以下就是这种情况。
情况 A
假设 A=10,000 美元,B=4,000 美元
玩家A不应冒险下注,下注金额不应超过A-2B-1。如果他对该类别没有信心,可以下注0美元。无论哪种方式,他都能确保获胜。在这种情况下,A的下注金额应在0美元到1999美元之间。
玩家B毫无希望,除非A下注过多而输掉比赛。在这种情况下,B应该考虑第三名的分数,并尽量保持领先,如果可以的话,争取第二名赢得2000美元,而不是第三名赢得1000美元。
情况 B
假设 A=10,000 美元,B=6,000 美元
A 的策略是预期 B 会全押,如果押对了,押注金额会覆盖 2B。然而,为了安全起见,他不应该押注过高,以免押错后金额低于 B。在这种情况下,他应该至少押注 2B - A + 1 和 AB - 1。在这种情况下,押注范围是 2,001 美元到 3,999 美元。
B 的策略是,如果答对了,至少要获得足够的分数才能超过 A,并提高总分。在本例中,A 的分数是 4,001 美元,B 的分数是 6,000 美元。
如果两位玩家都按照预期行事并遵循此策略,那么玩家 B 获胜的唯一可能性是 A 猜错而 B 猜对。这种情况的概率约为 19%。
情况 C
这里的事情变得更加复杂,涉及更多的博弈论和随机化。
假设 A=$10,000,B=$7,000。
在进一步探讨之前,重要的是估算“最终危险边缘”线索被正确解答的概率。根据第30至34季的数据,第一名玩家的正确率为52%,第二名玩家的正确率为46%。然而,这些概率是正相关的。以下是所有四种可能性的细分:
- 均正确:27%
- 第一名正确,第二名错误:25%
- 第一个位置错误,第二个位置正确:19%
- 两者都不正确,为 29%。
尽管前两位玩家的 Jeopardy 平均答对率为 49%,但两人都答对或都答错的概率却高达 56%。
当然,这些可以根据类别而改变,但让我们保持简单并使用上述概率。
在这种情况下,玩家B不必依赖A错而B正确。他可以下注较低金额,比如0美元,确保在A错的情况下获胜。换句话说,如果A的赌注足以弥补B的赔率(如果正确),那么如果A错而B的赌注为0美元,他就有可能跌破B的赔率。
然而,如果A预测B会押低注,比如0美元,那么A也可以押0美元来锁定胜局。两位玩家基本上都可以选择押低注还是押高注。A应该希望押与B相同的注,而B应该押与B相反的注。如果两位玩家都是完美的逻辑学家,他们就会随机做出决定。
在这种情况下,A 的高额投注应为 2B-A+1 至 AB-1,与情况 B 相同。在这种情况下,A 的低额投注应为 2,999 美元至 4,001 美元。
B 的高额投注应与情况 B 相同,如果正确,投注金额应足以超过 A。在本例中,分别为 3,001 美元和 7,000 美元。B 的低额投注应为 0 美元。
如果我跳过数学计算并直接讨论两位玩家的随机化策略,请原谅我。
玩家 A 选择高牌的概率为 62.3%,选择低牌的概率为 37.7%。
球员 B 应该处于高位,概率为 61.2%,处于低位,概率为 38.8%。
假设两个玩家都遵循这种随机化策略,并且概率配对正确,则玩家 A 获胜的概率为 65.2%。
如果玩家 A 的得分超过玩家 B 的 2/3,那么他获胜的概率就会上升到 81.0%。
在双重危险中下注时,两位玩家都应该牢记 2/3 规则的重要性。