概率 - 硬币
如果将一枚硬币抛 1000 次,那么正面总数在 452 到 548 范围内的概率是多少?
对于这个问题,我们可以使用二项分布的正态近似。正面朝上的次数的方差为 1000*(1/2)*(1/2)=250。因此标准差为 250 1/2 =15.8114。正面朝上次数少于 548 次的概率为 normdist((548+0.5-500)/15.8114) = 0.998920,其中 normsdist 是 Excel 函数,用于计算均值为 0、标准差为 1 的正态分布随机变量落入给定 Z 分数的概率。接下来,我们减去正面朝上次数少于 452 次的概率。结果为 normdist((452-0.5-500)/15.8114) = 0.001080。因此答案为 0.99892-0.00108 = 0.997840。再次强调,这只是一个近似值。实际答案是 0.997856,但推导起来更加繁琐。平均而言,在掷骰子游戏中确定一个点数后,玩家会多久再提出一个点数?
假设一个点有5/12的概率出现,那么它将会是6或8,4/12的概率是5或9,3/12的概率是4或10。出现6或8的概率是5/11,出现5或9的概率是4/10,出现4或10的概率是3/9。因此,假设一个点已经成立,那么出现该点的概率为:(5/12)*(5/11)+(4/12)*(4/10)+(3/12)*(3/9) = 40.61%。
巫师先生,如果50个不同的人把一枚硬币抛向空中8次,那么这50个人中,有多少人会连续8次抛出正面或反面?提前谢谢您。
任何一个人抛出8次正面或反面的概率是2*(1/2) 8 = 1/128。如果平均50个人这样做,其中0.39人会全部抛出正面或反面。至少一个人全部抛出正面或反面的概率是32.44%。
我有一袋100枚硬币,其中一枚是双面硬币。我随机抽取一枚硬币,然后观察它连续抛出10次正面。我抽到双面硬币的概率是多少?
这是一道典型的贝叶斯条件概率题。一般来说,给定 B 时 A 的概率是 A 和 B 的概率除以 B 的概率。在本例中,A 是连续抛 10 次正面,B 是掷出双头硬币。A 和 B 的概率是 1/100。这是因为掷出双头硬币的概率是 1/100,而如果真的掷出双头硬币,那么连续抛 10 次正面的概率是 100%。假设随机掷出一枚硬币,那么连续抛 10 次正面的概率是 (1/100)*1 + (99/100)*(1/2) 10。这是因为掷出双头硬币的概率是 1%,即掷出 10 次正面的概率是 100%,而掷出一枚公平硬币的概率是 99%,即连续抛出 10 次正面的概率是 (1/2) 10 。因此,假设你连续抛出 10 次正面,那么你选中两个正面硬币的概率为 0.01/(0.01*1 + 0.99* 0.000977) = 0.911843。
您对抛硬币投注有什么建议吗?
是的!我的建议是一开始就押正面朝上。据科学新闻在线报道,硬币落地时正面朝上的概率是51%。文章说,原因是抛出的硬币并非完美地绕轴旋转,有时看起来像在翻转,但实际上并没有。该假设仅适用于硬币被握在手掌中的情况,这样硬币的弹跳就不是问题了。文章还说,旋转的硬币落地时反面朝上的概率为80%,因为较重的正面会先向下沉。然而,我对此表示怀疑。我试了20次,得到了11次正面和9次反面。在20次旋转中,如果成功率为80%,得到9次或更少反面的概率是1/1775。
我相信我或许能解答旋转硬币的问题。十多年前,我在六年级时做过一个关于旋转硬币的科学项目。我在《Omni》杂志上读到,旋转硬币的速度非常快,几乎总能保证硬币反面朝上,因为硬币的侧面是向正面倾斜的。我尝试了数百次,结果几乎一致,除了两次硬币竖立着的时候。
浪费了好几个小时后,我终于发现我把它转得太快了,慢一点就能达到我想要的效果,也就是反面朝上。而且,这枚硬币也不是完全均匀的,从最薄的部分开始旋转似乎能增加一致性。几张满是胡扯的图表和一个装饰成硬币形状的巨大纸板圆圈,让我的科学课得了A,其他课都不及格,因为我完全不做作业。
因此,我已经通过十多年前做过的一个粗略的实验最终证明,你也许只是在胡思乱想,我几乎不记得任何事,也没有真正理解我当时在做什么。
好吧,我又试了一次,慢慢地把硬币转了100次。我说的“慢”是指从弹硬币到结果显现的时间至少有两秒,但不到五秒。我用的是一枚漂亮闪亮的2004-D版硬币。结果是52次正面,48次反面。所以我仍然不相信,无论硬币以何种速度旋转,都会出现反面的概率。
我理解的事件“等待时间”是该事件概率的倒数。我感兴趣的是计算用一个骰子掷出连续2的等待时间。在模拟中,我平均掷出42次。我该如何将其与掷出连续2的概率联系起来?
对于单个事件,如果概率为 p,则平均等待时间为 1/p,这的确没错。然而,对于连续事件,情况会变得更加复杂。设 x 表示最后一次掷出的结果不是 2 的状态。这也是初始状态。设 y 表示最后一次掷出的结果为 2 的状态。第一次掷出结果后,我们有 5/6 的概率仍处于状态 x,有 1/6 的概率处于状态 y。设 Ex(x) 表示从状态 x 开始的掷骰次数的预期,Ex(y) 表示从状态 y 开始的掷骰次数的预期。那么……
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y),且
Ex(y) = 1 + (5/6)*ex(x)
求解这两个方程...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*( 1 + (5/6)*Ex(x))
Ex(x) = 7/6 + (35/36)*Ex(x)
(1/36)*Ex(x)= 7/6
例如(x)= 36 *(7/6)= 42
因此连续两次掷出 2 的平均等待时间为 42 次。
我遇到了相同类型的问题,只有预期翻转才能得到两次正面,在我的数学问题网站上,请参阅问题 128。
假设我们有一个赌博游戏。一枚无偏硬币被反复抛掷。每次抛掷,我们需要支付 1 卢比。结果有两种可能:H 或 T。如果抛出正面和反面的差值为 3,我们将从赌徒那里得到 8 卢比。我们应该玩这个游戏吗?为什么?我们获胜的概率是多少?当我们掷出 7 或 9 卢比时,什么因素会影响获胜的概率?
我们将 x 称为从起点开始的翻转预期次数。
如果其中一方的翻转次数占多数,则我们将 y 称为剩余翻转的预期次数。
如果一方的翻转次数占多数,则我们将 z 称为剩余翻转的预期次数。
E(x) = 1 + E(y)
E(y) = 1 + 0.5*E(x) + 0.5*E(z)
E(z) = 1 + 0.5*E(y)
由此,用矩阵代数很容易得出 E(x) = 9,E(y) = 8,E(z) = 5。因此,平均需要抛掷 9 次才能使正面和反面的概率差达到 3。因此,对于每次抛掷都能赢取 1 卢比的人来说,8 卢比的赌注是一个不错的选择,因为他平均能赢 9 卢比,但只损失 8 卢比。对于赌徒来说,赌场优势是 11.11%。9 卢比的赌注是公平的,7 卢比的赌注则为 22.22%。
在您2006年3月13日的“问巫师”节目中,您给出了“卢比”游戏的三个公式。虽然答案在数学上是正确的,但我实在无法理解这三个公式是如何模拟这个问题的。您能解释一下您是如何得出这三个公式的吗?
很多人请我进一步解释一下我的答案。答案需要用到基本的矩阵代数知识。
首先将 x 定义为答案,或者直到正面和反面之间的差异为 3 为止的平均翻转次数。
令 y 为从一侧向上翻转一次的点开始的翻转预期次数。
令 z 为从一侧向上翻转两次的点开始的预期翻转次数。
第一次抛骰子后,其中一方将以一次抛骰子的优势占据多数。因此 x=1+y。
当任何一方领先一次抛掷时,另一方抛掷的结果要么与初始平局相同,要么是一方领先两次抛掷。两种结果的可能性相同。因此 y=1+0.5*x + 0.5*z
当任何一方领先两次抛掷时,再次抛掷将导致一方领先一次,或游戏结束。同样,两种结果的可能性相同。因此 z=1+0.5*y。
因此我们有三个方程和三个未知数:
(1)X= 1 + y
(2)Y = 1 + 0.5x + 0.5z
(3)Z = 1 + 0.5y
为了解决这个问题,我们首先将最后两个等式乘以 2 来去掉小数。
(1)X= 1 + y
(2)2Y = 2 + x + z
(3)2Z = 2 + y
我们将 (1) 中的 1+y 代入 (2) 中的 x。
2Y = 2 + 1 + y + z
(4)y=3+z
在 (3) 中不能用 3+z 代替 y
2z = 2 + 3 + z
z = 5
现在用 5 代替 (4) 中的 z 得到
(5)y = 3 + 5 = 8
将 y = 8 代入 (1) 中可得
(6)x = 9
一位朋友选择了一个三次抛硬币的顺序,结果是正面或反面,并让我选择我自己的(不同的)三次抛硬币顺序。我们抛一枚公平的硬币,直到出现我们想要的顺序。如果他选择HHH,我应该选择哪个顺序?在这个赌注中我的优势是什么?我该如何根据他选择的顺序来计算应该选择哪个顺序?
下表显示了根据玩家A和玩家B选择的所有可能模式,玩家A获胜的概率。
玩家 A 获胜的概率
| 玩家A | 玩家B | |||||||
| 哈哈哈 | 高血压 | 高血压 | 高温热电偶 | THH | 甲状腺激素 | 紧张性甲状腺功能亢进症 | 时间测试 | |
| 哈哈哈 | 1/2 | 2/5 | 2/5 | 1/8 | 5/12 | 3/10 | 1/2 | |
| 高血压 | 1/2 | 2/3 | 2/3 | 1/4 | 5/8 | 1/2 | 7/10 | |
| 高血压 | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/8 | 7/12 | |
| 高温热电偶 | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/4 | 7/8 | |
| THH | 7/8 | 3/4 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| 甲状腺激素 | 7/12 | 3/8 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| 紧张性甲状腺功能亢进症 | 7/10 | 1/2 | 5/8 | 1/4 | 2/3 | 2/3 | 1/2 | |
| 时间测试 | 1/2 | 3/10 | 5/12 | 1/8 | 2/5 | 2/5 | 1/2 | |
选择最佳模式的记忆方法是,他的第一和第二个选择应该分别对应你的第二个和第三个选择。你的第一个选择应该与你的第三个选择相反。例如,如果对手选择HTT,你的第二个和第三个选择应该是HT。你的最后一个选择是T,所以对于HHT模式,你的第一个选择应该是H。按照这个策略,你的获胜概率将是2/3到7/8,具体取决于对手选择的模式。
你好,我叫帕蒂。你的网站很棒,而且你看起来知识渊博。你绝对是我在赌场里想要的那种人!!!!我想知道你能不能帮我。我跟男朋友说我想在网上找个问题答案。如果你能帮我,那我可就太有面子了。
我的男朋友是个钱币收藏家。他买了一袋小麦币。我自己对钱币不太了解。(他慢慢教我)但他说,他很惊讶那袋钱币里竟然没有某一年份的钱币,因为这种钱币太常见了。他说这种事情发生的概率简直是十亿分之一。我告诉他,我会试着问问办公室里那些自称天才的人!如果他们不知道,我就试着在网上查一下。我偶然遇到了你。
无论如何,如果你能帮忙,我将不胜感激。袋子里大约有5500枚一分硬币。美国所有铸币厂铸造的小麦币一分硬币总数为242.67亿枚。铸造的1955年版一分硬币(他要找的那枚)数量是3.3亿枚。我办公室里的一些人说还有其他因素,比如人口统计,铸币厂可能没有分发所有一分硬币等等。…… ...
您的铸币数量与Mountain View Coins的铸币数量接近。假设所有小麦一分硬币入袋的概率相同,那么任何一分硬币中不是 55 面值的概率为 (24,267,000,000-330,000,000)/24,267,000,000 = 0.986401286。5500 枚硬币中不是 55 面值的概率可以非常近似地计算为 0.986401286 5500 = 507,033,772,284,213,000,000,000,000,000,000,000 分之一。
我爸爸是个钱币收藏家,所以我向他寻求了这方面的帮助。他是这样说的:
这是我的猜测。1955年,费城铸造了少量林肯一美分硬币,但日期却印了两次。没有人知道确切的数量。在发现错误之前,它们与其他一美分硬币混在一起流通。一枚未流通的硬币如今价值约2000至6000美元。我怀疑那袋“小麦”硬币里的所有1955年版硬币已经被某个寻找双模硬币的人全部淘光了。这里有一张照片: 1955年双模正面一美分硬币。
请注意,本网站出售的是“麦穗”版,可以肯定的是,在硬币被经销商收集后,一些年份的硬币已经被剔除。我原本以为那些非双模版的1955年版硬币会被归还收藏,但它们或许会被单独出售或熔化处理。如今,麦穗版便士中的铜比一美分值钱得多。这就是为什么他们在几十年前就改用镀铜锌版便士的原因。也有可能,铸币厂自己决定不发行许多1955年版硬币,而是在铸造后将其熔化处理,以避免人们对稀有的双模版硬币产生疯狂的抢购。铸币厂和邮局一直对印刷错误感到尴尬,并试图阻止它们流通。
在您上一篇专栏文章中,您说过“5500 枚硬币不是 55 的概率可以非常接近地近似为 0.9864012865500 = 507,033,772,284,213,000,000,000,000,000,000,000 分之 1”。
我假设“近似”是因为当你处理这5500枚硬币时,移除的影响是存在的。移除的影响微乎其微!这是一个很好的例子,说明当你移除非目标硬币时,目标硬币出现的可能性会降低,因为与不正当游戏(即目标硬币被移除)的概率相比,移除的影响非常小。
是的,我说的是“非常接近”,因为世界上的硬币数量有限。从袋子里取出一枚非55面值的硬币,其移除效应会增加袋子里其他所有硬币都是55面值的硬币的概率。如果我没说“非常接近”,至少会有三个人写信来纠正我。当然,这只是一个极其微小的误差,但我的很多读者都是完美主义者,哪怕是最轻微的错误,他们也会对我大加指责。
房间里有两张桌子。右边的桌子上有100枚硬币,其中20枚H面朝上,其余80枚T面朝上。另一张桌子上没有硬币。目标是想办法移动硬币,使两张桌子上H面朝上的硬币数量相等。房间很暗,你既看不到硬币,也无法触摸它们来判断它们是“朝上”还是“朝下”。
请访问我的另一个网站 mathproblems.info 寻找解决方案(剧透警告!)
我朋友愿意跟我打赌20美元,他给了我3比1的赔率,如果我抛硬币100次,结果一定是50次正面和50次反面。如果正面和反面都出现,我就赢60美元;如果反面出现,我就欠他20美元。我应该接受这个赌注吗?另外,如果50/50不是最有可能的结果,还有其他更有可能出现的结果吗(比如51/49)?
正面和反面正好各出现50次的概率是 (100,50)*(1/2) 100 = 7.96%。公平赔率是11.56比1。因此,3比1的赔率非常糟糕,赌场优势高达68.2%。这可不是你的朋友。50/50是正面和反面最有可能出现的概率。一个有趣的赌注是正面/反面的次数是否会在47到53之间。落在这个范围内的概率是51.59%。如果你能找到一个赌徒押注总数会落在这个范围之外,那么在等额投注的情况下,你将获得3.18%的优势。
下表显示了 30 至 70 次正面/反面的概率。
100 次抛掷中全部正面/反面的概率
| 正面/反面 | 可能性 |
|---|---|
| 30、70 | 0.000023 |
| 31, 69 | 0.000052 |
| 32, 68 | 0.000113 |
| 33, 67 | 0.000232 |
| 34, 66 | 0.000458 |
| 35、65 | 0.000864 |
| 36, 64 | 0.001560 |
| 37, 63 | 0.002698 |
| 38, 62 | 0.004473 |
| 39, 61 | 0.007111 |
| 40、60 | 0.010844 |
| 41, 59 | 0.015869 |
| 42, 58 | 0.022292 |
| 43, 57 | 0.030069 |
| 44, 56 | 0.038953 |
| 45,55 | 0.048474 |
| 46, 54 | 0.057958 |
| 47, 53 | 0.066590 |
| 48, 52 | 0.073527 |
| 49, 51 | 0.078029 |
| 50 | 0.079589 |
在 n 次试验中,w 次获胜的概率的一般公式为 combin(n,w) × p w × (1-p) (nw) = [n!/(w! × (nw)!] × p w × (1-p) (nw) ,其中每次获胜的概率为 p 。
如果我抛硬币 1,000 次,那么连续看到至少 10 次正面或反面的概率是多少?
你问得真有意思;另一位读者刚刚给我发了一篇关于这个主题的学术论文。这篇论文包含下图,显示概率约为 62%。
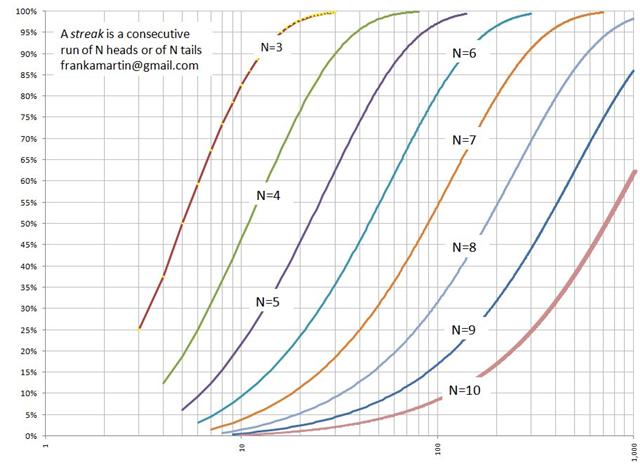
有关该主题的更多信息,请参阅弗兰克·马丁 (Frank Martin) 撰写的《在赌场中遭遇如此糟糕连胜的几率有多大?》 (483K)。
如果将一枚硬币抛 100 次,那么至少有一次连续出现 7 次正面的概率是多少?
我不知道这个问题是否有一个简单的、非递归的表达式来表达。但是,有一个简单的递归表达式来表达。
f(n)= pr(第一次抛反面的个数)×f(n-1) +
pr(第一次抛掷正面,第二次抛掷反面)×f(n-2) +
pr(前两次抛掷的正面,第三次抛掷的反面)×f(n-3) +
pr(前三次抛掷的正面,第三次抛掷的反面)×f(n-4) +
pr(前四次抛掷的正面,第四次抛掷的反面)×f(n-5) +
pr(前五次抛掷的正面,第五次抛掷的反面)×f(n-6) +
pr(前六次抛掷的正面,第六次抛掷的反面)×f(n-7) +
pr(前 7 次抛掷的正面次数) =
(1/2)×f(n-1)+
(1/2) 2 ×f(n-2)+
(1/2) 3 ×f(n-3)+
(1/2) 4 ×f(n-4)+
(1/2) 5 ×f(n-5)+
(1/2) 6 ×f(n-6)+
(1/2) 7 × f(n-7) +
(1/2) 7
在哪里:
f(n)=n次翻转内成功的概率。
pr(x)=x发生的概率。
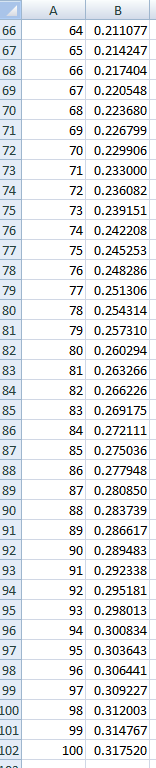
电子表格非常适合解决这类问题。在下面的电子表格截图中,我在单元格 B2 到 B8 中输入了概率 0,因为在 6 次或更少的抛掷次数内不可能连续出现 7 次正面。在单元格 B9 中,我输入了以下公式:
=(1/2)*B8+(1/2)^2*B7+(1/2)^3*B6+(1/2)^4*B5+(1/2)^5*B4+(1/2)^6*B3+(1/2)^7*B2+(1/2)^7
然后我把它从单元格B10复制粘贴到单元格B102,相当于翻转100次。这个概率是0.317520。随机模拟证实了这一点。
 |  |
这篇文章最初发表后,Rick Percy 与我分享了他的矩阵代数解法。以下是我自己的解释。我假设读者已经了解矩阵代数的基础知识。
首先,在任何时候,弹球器可能处于八种状态:
p 1 = 成功的概率,假设从当前点开始你需要再掷出 7 个正面。
p 2 = 成功的概率,假设你需要从当前点开始再出现 6 个正面。
p 3 = 成功的概率,假设您需要从当前点开始再出现 5 个正面。
p 4 = 成功的概率,假设您需要从当前点开始再出现 4 个正面。
p 5 = 成功的概率,假设您需要从当前点开始再出现 3 个正面。
p 6 = 成功的概率,假设您需要从当前点开始再出现 2 个正面。
p 7 = 成功的概率,假设您需要从当前点开始再出现 1 个正面。
p 8 = 成功的概率,假设您不需要更多的正面 = 1。
我们将矩阵 S n定义为第 n次翻转后处于每个状态的概率。S 0表示第一次翻转之前的概率,其中有 100% 的概率处于状态 0。因此 S 0 =
| 1 0 0 0 0 0 0 0 |
令 T 为两次连续翻转的变换矩阵,即从 S n到 S n+1 ,其中 S n+1 = T × S n
- 如果您处于状态 1,那么在一次翻转之后,您有 0.5 的机会处于状态 2(正面),并且有 0.5 的机会保持在状态 1(反面)。
- 如果您处于状态 2,那么在一次翻转之后,您有 0.5 的机会处于状态 3(正面),并且有 0.5 的机会返回到状态 1(反面)。
- 如果您处于状态 3,那么在一次翻转之后,您有 0.5 的机会处于状态 4(正面),并且有 0.5 的机会返回到状态 1(反面)。
- 如果您处于状态 4,那么在一次翻转之后,您有 0.5 的机会处于状态 5(正面),并且有 0.5 的机会返回到状态 1(反面)。
- 如果您处于状态 5,那么在一次翻转之后,您有 0.5 的机会处于状态 6(正面),并且有 0.5 的机会返回到状态 1(反面)。
- 如果您处于状态 6,那么在一次翻转之后,您有 0.5 的机会处于状态 7(正面),并且有 0.5 的机会返回到状态 1(反面)。
- 如果您处于状态 7,那么在一次翻转之后,您有 0.5 的机会处于状态 8(正面),并且有 0.5 的机会返回到状态 1(反面)。
- 如果您处于状态 8,那么您就取得了成功,并且将以 1.0 的概率保持在状态 8。
将所有这些放在转换矩阵 T = 的形式中
| 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.5 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.5 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 |
为了得到一次翻转后每个状态的概率...
(1) S1 = S0 ×T
翻转两次之后怎么样?
(2) S2 = S1 ×T
让我们用方程 (2) 代替方程 (1)...
(3) S2 = S0 ×T×T= S0 × T2
那么翻转 3 次之后呢?
(4) S3 = S2 ×T
将方程 (3) 代入方程 (4)...
(5) S3 = S0 × T2 ×T= S0 × T3
我们可以一直这样做,直到第 100 次翻转之后的状态......
S 100 = S 0 × T 100
那么,T 100是多少?在计算机出现之前,弄清楚这些数字一定非常困难。然而,借助 Excel 的 MMULT 函数,经过大量的复制粘贴,我们发现 T 100 =
| 0.342616 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.317520 |
| 0.339863 0.170617 0.085653 0.042999 0.021586 0.010837 0.005440 0.323005 |
| 0.334379 0.167864 0.084271 0.042305 0.021238 0.010662 0.005352 0.333929 |
| 0.323454 0.162380 0.081517 0.040923 0.020544 0.010313 0.005178 0.355690 |
| 0.301693 0.151455 0.076033 0.038170 0.019162 0.009620 0.004829 0.399038 |
| 0.258346 0.129694 0.065109 0.032686 0.016409 0.008237 0.004135 0.485384 |
| 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.002753 0.657384 |
| 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 |
右上角的项显示了翻转 100 次后处于状态 8 的概率,即 0.317520。
你听说过一个澳大利亚板球运动员的故事吗?他连续35场比赛都预测错了硬币,直到第36场比赛才预测正确。这种情况发生的概率有多大?
你提到这件事之前我都没听说过。你指的是喜鹊队(Magpies)青少年板球运动员克里斯蒂·佩林(Kristy Perrin)的精彩故事。她确实连续35次抛硬币预测错误。准确预测35次或更多次的概率是(1/2) 35 = 34,359,738,368分之一。换个角度来看,中强力球的概率是195,249,054分之一。这比连续35次抛硬币预测错误的可能性高出176倍。
您对抛硬币投注有什么建议吗?
是的!押注抛硬币者手中朝上的一面。Persi Diaconis、Susan Holmes 和 Richard Montgomery 合著的学术论文《抛硬币的动态偏差》得出的结论是,硬币落地时朝上的概率为 51%。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
平均而言,在一场50/50的游戏中,需要多少次尝试才能连续输两次?连续输3次、4次、n次呢?
我们先来解决两次损失的情况。
令 x 为从开始或每次获胜后未来翻转的预期次数。
令 y 为一次失败后未来抛掷的预期次数。
我们可以建立以下两个方程:
(1)x = 1 + .5x + .5y
一代表玩家必须抛硬币来改变状态。获胜的概率为 50%,保持在状态 x。失败的概率为 50%,进入状态 y。
(2)y = 1 + .5x
再次从状态 y 开始,1 表示在该点进行翻转。获胜的概率为 50%,返回状态 x。失败的概率为 50%,游戏结束,无需再次翻转,因此隐含的概率为 0.5*0。
将两个方程乘以 2 并重新排序可得:
(3)x - y = 2
(4)-x + 2y = 2
将两个方程相加可得:
(5)y=4
将其代入 (1) 至 (4) 中的任何方程,得到 x=6。
对于三损失的情况,将三种可能的状态定义为:
令 x 为从开始或每次获胜后未来翻转的预期次数。
令 y 为一次失败后未来抛掷的预期次数。
令 z 为两次失败后未来抛掷的预期次数。
初始方程为:
x = 1 + .5x + .5y
y = 1 + .5x + .5z
z = 1 + .5x
我们可以将初始状态设置为矩阵形式:
| 0.5 | -0.5 | 0 | 1 |
| -0.5 | 1 | -0.5 | 1 |
| -0.5 | 0 | 1 | 1 |
如果你还记得矩阵代数,我们可以用行列式(A)/行列式(B)来解 x,其中
A =
| 1 | -0.5 | 0 |
| 1 | 1 | -0.5 |
| 1 | 0 | 1 |
B =
| 0.5 | -0.5 | 0 |
| -0.5 | 1 | -0.5 |
| -0.5 | 0 | 1 |
| 0.5 | -0.5 | 0 |
| -0.5 | 1 | -0.5 |
| -0.5 | 0 | 1 |
Excel 有一个方便的行列式函数:=mdeterm(range)。在本例中,x = mdeterm(矩阵 A)/mdeterm(矩阵 B) = 1.75/0.125 = 14。
我们可以使用递归来处理更多连续失败的情况。假设是 4 次。根据上文所述,平均需要抛硬币 14 次才能连续失败 3 次。此时,硬币将再次抛出,重新开始的概率为 50%。因此:
x = 14 + 1 + x/2
x/2 = 15
x = 30
换句话说,在前一个答案上加一,然后加倍。
不难看出其中的规律。连续 n 次失败的期望抛掷次数是 2 n+1 -2。
这个问题是在我的“拉斯维加斯巫师”论坛上提出并讨论的。
假设一枚公平硬币被抛掷 n 次,出现至少一次 t 次反面的概率是多少?
答案是 1-F (t) n+2 /2 n ,其中 F (t) n是 t 步斐波那契数列中的第 n 个数字。
你可能会问,斐波那契数列是什么?它的第一个数字是 1。在 t 步序列中,每个后续数字都是前 t 个数字之和。假设第一个数字之前的任何数字都是 0。
让我们看一个两步序列。第一个数字是 1。第二个数字是前两个数字之和。假设 1 前面有一个 0,所以第二个数字是 0+1=1。第三个数字是 1+1=2,第四个数字是 1+2=3,第五个数字是 2+3=5。
前十二个二步斐波那契数列为:1、1、2、3、5、8、13、21、34、55、89、144。
我们举个例子,抛十次硬币,至少有一次连续掷出两次反面的概率是多少?
我们使用两步斐波那契数列,因为我们只需要两次反面。数列中的第 12 个数字(比翻转次数多 2 个)是 144。因此,答案是 1-F (2) 10+2 /2 10 = 1 - 144/2 10 = 1 - 144/1024 = 85.94%。
在 20 次抛掷中,连续出现 5 次反面的概率是多少?
前 22 个 5 步斐波那契数列为 1、1、2、4、8、16、31、61、120、236、464、912、1793、3525、6930、13624、26784、52656、103519、203513、400096、786568。
因此答案为 1 - F (5) 20+2 /2 20 = 1 - 786,568/1,048,576 = 1 - 75.01% = 24.99%。
我在Wizard of Vegas论坛上讨论过这个问题。
有一枚有偏差的硬币,正面朝上的概率为 60%。它被抛掷,直到连续出现两次正面或两次反面。先出现两次正面的概率是多少?
这是答案和解决方案(PDF)。
有关此问题的讨论,请访问我在Wizard of Vegas 的论坛。
巫师,我向你挑战一个赌注。规则如下:
- 你可以选择任何你喜欢的正面(H)和反面(T)的图案。例如,HTT。
- 在揭示你的图案后,我将选择我的图案。
- 我们会反复抛硬币,直到出现一种图案。选择该图案的人获胜。
- 我给你 3 比 2 的赔率。
你接受吗?我愿意做多少次就做多少次。
不。不过,尝试得不错。后手拥有巨大的位置优势。以下是后手的策略及其获胜概率。
Odiusgambit 游戏策略
| 玩家 1 | 玩家 2 | Pr. 玩家 2 获胜 |
|---|---|---|
| 哈哈哈 | THH | 87.50% |
| 高血压 | THH | 75.00% |
| 高血压 | 高血压 | 66.67% |
| 高血压 | THH | 75.00% |
| THH | 高温热电偶 | 75.00% |
| 甲状腺激素 | 紧张性甲状腺功能亢进症 | 66.67% |
| 紧张性甲状腺功能亢进症 | 高温热电偶 | 75.00% |
| 时间测试 | 高温热电偶 | 87.50% |
如上表所示,我获胜的最佳机会(或者说您获胜的最差机会)是选择 THT 或 HTH,此时我的获胜机会仍然只有 1/3。我应该以 2 比 1 的赔率进行公平投注,因此如果只以 3 比 2 的赔率进行投注,那么您的优势就有 16.67%。
以下是记住玩家二策略的方法。令 P(x) 表示玩家一在位置 x 的选择。令 O(x) 表示玩家一在位置 x 的选择的反方向。玩家二的选择应该始终为:O(2) - P(1) - P(2)。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
如果抛一枚公平硬币40次,出现5次正面和5次反面的概率是多少?“1连”表示至少出现1次正面,“5连”表示至少出现5次反面。正面和反面的连次不必相邻。
请点击下面的按钮获取答案。
这是我的解决方案(PDF)。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
亨利和汤姆决定赌一把抛硬币。亨利掷正面赢,汤姆掷反面赢。
每次抛硬币要1美元,他们实在无聊,所以决定抛一百万次。每次抛完后,输的人会给赢的人开一张支票,作为最终的余额。支票金额的期望值是多少?
答案的一般公式是 sqrt(方差 * (2/pi))。
在这种情况下,方差为 1,000,000。因此,实际结果与预期结果之间的预期绝对差为 sqrt(1,000,000 × (2/pi)) =~ 797.88456080286535587989211986876373695171726 232986931533185165934131585179860367700250466 781461387286060511772527036537102198390911167 448599242546125101541269054116544099863512903 269161506119450728546416733918695654340599837 28381269120656178667772134093073。
我在Ask the Wizard #358中提出了一个相关问题,这将有助于显示我从哪里得到 sqrt(2/pi) 项。
这个问题是在Wizard of Vegas论坛上提出并讨论的。
假设一家赌场有一款基于公平抛硬币的游戏,赔率相同。一位玩家希望以每次1美元的赌注玩一百万次。他应该投入多少钱才能有50%的概率不破产?
让我们首先回答这个问题:假设玩家的资金无限,那么在一百万次抛掷之后,玩家亏损超过 x 个单位的概率是多少。
由于这是一个公平的赌注,一百万次抛掷后的平均赢利为零。每次抛掷的方差为1,因此一百万次抛掷的方差为一百万。因此,一个标准差为 sqrt(1,000,000) = 1000。
我们可以使用 Excel 函数 =norm.inv(probability,mean,standard deviation) 来计算所需的资金。例如,如果我们输入 =norm.inv(.25,0,1000),我们会得到 -674.49。这意味着,如果在一百万次抛掷之后,玩家有 25% 的概率输掉 674 或更多。请记住,这只是一个估计值。为了得到正确的答案,我们应该使用二项分布,但如果抛掷了一百万次,这将非常繁琐。
如果玩家带着674美元上桌,他很可能在百万翻倍之前就把钱花光。如果他能继续赊账,他或许能翻盘,最终输掉的钱少于674美元。事实上,一旦玩家的赔率是-674美元,那么在未来的某个时间点,他最终输掉的钱有一半的可能性会高于或低于-674美元。
因此,如果玩家可以赊账玩,则可能出现三种结果。
- 玩家的水平永远不会低于-674。
- 玩家在某个时刻跌至 -674 以下,但恢复并最终超过 -674。
- 玩家在某个时刻跌至 -674 以下,继续玩并输得更多。
我们已经确定情景 3 的概率为 25%。
场景 2 的概率必须与场景 3 的概率相同,因为一旦玩家落后 -674,那么在一百万次抛掷之后,他有 50% 的机会达到或低于该点。
场景 1 是唯一的其他选择,其概率必须为 100%-25%-25% = 50%。
如果玩家永远不会低于 674 的概率是 50%,那么低于该数额的概率一定是 100%-50% = 50%。
因此,我们对原始问题的答案是 674 美元。
我在Wizard of Vegas论坛上提出并讨论了这个问题。


