概率 - 牌
我在网上玩百家乐,75 手牌中庄家赢了 52 手,闲家赢了 23 手。差额为 29,发生这种情况的概率是多少?
首先,我假设您不计算平局。换句话说,您的意思是 75 手牌不平局。75 手牌不平局的可能性很小。在 75 手牌中,庄家获胜的预期次数为 38.00913745。标准差是 75、庄家获胜概率和闲家获胜概率乘积的平方根。假设没有平局,庄家获胜的概率为 0.506788499,闲家获胜的概率为 0.493211501。因此标准差为 4.329727904。然后,您必须对二项分布进行半点修正,并在标准正态分布表中查找 Z 统计量(此步骤留给读者)。最终答案是,庄家赢 52 次或以上的概率是 0.0009。您的问题也考虑了庄家赢 23 次或更少(也相差 29 次或更多)的可能性,这个概率是 0.0004。所以最终答案是,相差 29 次或更多的概率是 0.0013,即 769 分之一。
在计算加勒比梭哈扑克玩家与庄家手牌的组合时,我仅得出3,986,646,103,440种,而你的结果是19万亿等,恰好相差5倍。我使用了组合函数(52,5)*组合函数(47,5)。哪里出错了?谢谢,我认为你的网站非常棒。
感谢夸奖。你的计算偏差了五倍,因为庄家可以任意展示五张牌中的一张。换句话说,庄家的手牌顺序确实重要,因为第一张牌是明牌。正确的总组合数推导应为combin(52,5)*47*combin(46,4) = 19,933,230,517,200。
抽三张牌拿到对⼦与抽五张牌扑克拿到full house葫芦的概率是多少?
在这种状况拿到full house葫芦有两种⽅式: (1)抽到三条、或者(2)对⼦再抽到⼀张同点数牌、还有另⼀个对⼦。我将假设你会舍弃三张各⾃不同的单牌。 ⾸先, 让我们先从(1)的排列组合总数着⼿算起。那⾥只剩下3种花⾊的3种点数牌(记住你已经舍弃3张各⾃不同的单牌)、4种花⾊的9种点数牌。其排列组合总数为 3*combin(3,3)+9*combin(4,3) = 3*1 + 9*4 = 39. 接下来, 让我们算⼀下(2)状况的排列组合总数。从既有对⼦再加上⼀张相同点数牌、还剩下有2张牌。剩余的3张牌当中形成3种点数的对⼦有combin(3,2)种⽅式, 剩余的4张牌当中再形成⼀个对⼦有combin(4,2)种⽅式。所以在(2)的排列组合总数为2*(3*combin(3,2)+9*combin(4,2)) =2*(3*3 + 9*6) = 126. 在(1)与(2)状况之下形成full house葫芦的⽅式总和为39+126=165. 第⼆轮抽牌要从3张牌选取的⽅式有combin(47,3)=16,215种。拿到full house葫芦的机率为抽牌⽅式除以排列组合总数, 为165/16,215 = 0.0101758, 或者差不多是98分之⼀。 欲知combin()函数的更多资讯, 请参阅我的 扑克中的机率 专⻚。
我每周会和朋友玩⼀次扑克(五张牌梭哈、七张牌梭哈)。我们同桌共有七位玩家。随着玩家⼈数的增多、从单副52张牌组当中拿到牌⾯的机率似乎就会骤减。你是否有数学上的公式可以指引我?
没有, ⽆论赌桌上有多少位玩家、拿到给定牌⾯的机率都是相同的。没⻅到的牌就是⼀张没出现的牌, 不管那张牌是被另⼀位玩家拿到或者还藏在牌组当中。
最近有人告诉我一个难以置信的故事!!我的一个朋友告诉我,在他家玩扑克牌友谊赛时,他和他的朋友在同一手牌中都抽到了顺子,而且没有抽任何牌!!(五张牌抽牌)我觉得这难以置信,我从你们的网站上计算出,抽到顺子的概率大约是65000比1,那么在6个人一起玩(没有抽任何牌)的情况下,一手牌中抽到2张顺子的概率是多少呢?
在三张牌扑克中,如何计算出获得以下牌型的概率:(1)Q 高牌、(2)K 高牌、(3)A 高牌?
我将首先计算出 K 高牌,然后简要展示其他两个牌型的公式。概率是 K 高牌的数量除以牌型总数。小于 K 的牌型数量为 11。K 高牌必须具有两个不同的等级。从 11 张牌中排列 2 张的方法数为combin (11,2) = 55。但是,其中一个组合是 K-Q-J,可以组成顺子,因此减去该组合,还剩下 54 种不能组成顺子的组合。接下来,每个等级有四种花色,即 4 3 =64 种可能的花色组合。但是,这 64 种花色中有四种可以组成同花,因此还剩下 64-4=60 种花色组合。因此,K 高牌的组合总数为 54*60=3240。从 52 张牌中排列 3 张,一共有 combin(52,3)=22,100。因此,组成 K 高牌的概率为 3,240/22,100 = 0.1466063。组成 A 高牌的概率为:(combin(12,2)-2)*(4 3 -4)/combin(52,3)=0.1737557。注意,由于 a-2-3 和 qka 顺子的存在,所以这里用 -2 而不是 -1。
皇后高牌的概率为:(combin(10,2)-1)*(4 3 -4)/combin(52,3)=0.119457。
拿到皇家同花顺的概率是多少?拿到连续皇家同花顺(顺着或逆着)的概率是多少?
皇家同花顺的概率等于可能的皇家牌数(每种花色各一张)除以从52张牌中选出5张的方式数,即combin (52,5)=2,598,960。因此,答案是4/2,598,960 = 0.00000153908,即649,740分之一。
连续同花大顺的概率等于(花色数)*(方向数)/(52 张牌中 5 张牌的排列组合总数)= 4 * 2 /排列(52,5) = 8 / 311,875,200 = 8 / 可能的同花大顺数量(即 4 张(每种花色一张))乘以可能的方向数,再除以从 52 张牌中抽出 5 张牌的组合方式数,即排列(52,5) = 311,875,200。因此,答案为 4/311,875,200 = 0.00000002565,即 38,984,400 分之一。
我喜欢用美元玩“说谎者扑克”游戏。请问一张钞票上出现任意一个相同数字的概率是多少?谢谢。如果我和三个人一起玩,出现任意一个数字的概率是多少?
首先,让我来回答一个未被提及的问题:某个特定数字在一张随机钞票上出现 n 次的概率。一张钞票上有 8 位数字,因此特定数字出现 n 次的概率为 combin(8,n)*0.1 n *0.9 8-n /10 8 。下表显示了特定数字出现 0 到 8 次的概率。
骗子扑克中的特定数字赔率
| 数字 | 可能性 |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| 全部的 | 1.00000000 |
下表列出了每种可能出现的钞票类型的概率,按每种类型的数量分类。例如,序列号 66847680 的钞票可能出现一张三张同点钞票、一张对子钞票和三张单张钞票,概率为 0.1693440。
说谎者扑克中的一般概率
| 8 橡木 | 7 橡木 | 6 橡木 | 5 橡木 | 4 橡木 | 3 橡木 | 2 橡木 | 1 橡木 | 可能性 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0.0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0.0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0.3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| 全部的 | 1.0000000 | |||||||
橡木 = “一种”
欲了解更多信息,请参阅我的“骗子扑克”页面。
用一副 52 张牌的扑克牌,抽出一对 J 的概率是多少?
假设您抽五张牌,并且所有牌中恰好有两张 J,那么概率就是 combin(4,2)*combin(48,3)/combin(52,5) = 6*17296/2598960 = 3.99%。
在牌九扑克中拿到三对的概率是多少?这个概率比三条大还是小?
不算三条和两对,以下是凑成三对的方式和组合数。
没有通配符:combin(13,3)*10*6 3 *4 =2471040
百搭牌用于对抗一对 A:combin(12,2)*10*6 2 *4 2 = 380,160
外卡用作单张 A 牌:combin(12,3)*6 3 = 47,520
总组合数为 2,898,720。这还不到三条组合数(747,0676)的一半。
根据你的公式,皇家同花顺的赔率是4/2,598,960 = 1/649,740。所以,如果我和庄家一对一玩加勒比梭哈,我的牌和庄家的牌的和应该相等,即649,740*2=1,299,480。因此,根据数学计算,1,299,480手牌之后应该会出现两手皇家同花顺。请告诉我我是否理解正确。
你说得对,平均每649,740手牌中会出现一次皇家同花顺,而1,299,480手牌中皇家同花顺的预期出现次数是2次。然而,这只是平均值。每一手牌过去,你距离拿到皇家同花顺都只有一步之遥。每局独立试验都具有这种无记忆特性,所以皇家同花顺永远不会过期。
在 1,299,480 手牌中出现零张王室牌的概率为 13.53%。
您好,我是牌九扑克的常客,我注意到您的网站上有很多关于这个游戏的精彩信息。前几天我和一个朋友玩牌九,他拿到了一手9高牌,我认为这是最低的牌型了。我玩牌九这么多年,只见过一次这种情况。五手牌之后,他又拿到了一模一样的牌(2-3-4-5-7-8-9)。我们简直不敢相信,也很好奇这种情况发生的概率有多大,所以想问问您。感谢您抽出时间,也感谢您精彩的网站。
形成9高牌的排列方式有两种,一种是您提到的,另一种是2-3-4-6-7-8-9。无法形成同花的花色组合数为4 7 -4*(combin(7,5)*3^2+6*3+1) = 15,552。因此,9高牌的概率为2*15,552/combin(53,7) = 31,104/154,143,080,即9,911分之一。如果您只玩五次,获得两手9高牌的概率为9,826,685分之一。我认为这种情况只是巧合,而不是随机数生成器或程序编码的故障。
我的问题是关于赌场战争中尼亚加拉赌场规则中庄家优势和风险因素的计算(例如,加注时赔付3-1,输掉原始赌注)。您是如何得出这些数字的?我现在正在尝试计算它们。我遇到了麻烦。感谢您的帮助。
设d为牌组数量。第一轮平局的概率为(4*d-1)/(52*d-1)= 0.073955。第二轮平局的概率为12*4*d/(52*d-2)*(4*d-1)/(52*d-3)+(4*d-2)/(52*d-2)*(4*d-3)/(52*d-3) = 0.073974。设p 1为第一轮平局的概率,p 2为第二轮平局的概率。则玩家回报为p 1 *(2*p 2 +(1-p 2 )/2*(1-2))= -0.023301。乘以-1,则庄家优势为2.33%。我希望我没有太快地回顾这一点。
你能告诉我加勒比地区19,933,230,517,200种组合数是怎么算出来的吗?我按照你的五张牌扑克组合数算出了2,598,960种组合数。接下来我该怎么继续呢?先谢谢了。
您正确计算了玩家组合数: combin (52,5)=2,598,960。由此推算,庄家可能的组合数为 combin(47,5)=1,533,939 种。然后,五张庄家牌中任意一张都可以正面朝上。因此,2,598,960*1,533,959*5=19,933,230,517,200 种组合数。
首先,我想说,我觉得您的网站真的很棒。我已经告诉了几个人,希望他们也能试试。祝您继续成功。我也很喜欢 WinPoker 的链接。我非常喜欢 WinPoker,所以订购了它。这是一个很棒的程序。我有一个问题希望您能帮助我。我一直在尝试计算七张牌梭哈中每手牌出现的次数。我有一份您的七张牌牌型表,但我对计算这些数字的数学原理很感兴趣。我能计算出五张牌的数字,但七张牌的数字让我很困惑。我想发送一个包含我的数字的 Excel 2000 文件。我还想知道如何计算一副 53 张牌、带有百搭牌的扑克牌中顺子的数量。救命!!!
谢谢你的赞美。我同意七张牌梭哈的点数计算起来很难。所以我用电脑来算。我的程序会计算所有可能的组合,并为每个组合计分。牌九扑克中的百搭顺子数量是 11*(4 4 -4)+10*3*(4 4 -4)=10332。加上 10200 个自然顺子,总数是 20532。
我了解加勒比梭哈扑克或Let it Ride牌桌上任何一个人拿到皇家同花顺的概率,以及这些概率是如何计算出来的。但我的问题是:作为旁观者,在任何特定牌局中,看到牌桌上任何一位玩家拿到这些牌的概率是多少?我猜想这取决于牌局数量……难道仅仅是个人的概率乘以牌局数量?比如,如果牌桌上有4位玩家,看到任何一手牌拿到皇家同花顺,就意味着拿到皇家同花顺的概率是4倍?我有点困惑!
你的方法近似效果不错。然而,按照这个逻辑,抛硬币时,每3个人中至少有一个人抛出正面的概率是3*50%=150%。假设事件独立,n次试验中至少有一次成功的概率(每次成功的概率为p)是1-(1-p) n 。在抛硬币的例子中,这个概率是1-0.5 3 =0.875。在四人玩加勒比梭哈扑克的情况下,至少有一次出现同花大顺的概率是1-(1-4/2598960) 4 = 0.00000615629。然而,由于所有牌都来自同一副牌,因此事件并非独立事件。确定确切的正确答案需要非常复杂的数学计算,而近似值应该非常接近正确答案。
在牌九扑克中,拿到七张自然同花顺的概率是多少?我在赌场工作,15年来第一次遇到这种情况。那位幸运的顾客赢了4万美元。
自然同花顺共有 32 种可能(4 个等级乘以 8 种可能的 7 张牌组合)。从 53 张牌中抽出 7 张牌的可能组合共有 combin(53,7) = 154143080 种。因此答案是 32/154143080,即 4816971 分之 1。
在三张牌扑克中连续两手获得相同的同花顺(等级和花色)的概率是多少?
第一手牌拿到同花顺的概率是 4*12/combin(52,3) = 48/22100 =~ 0.0022。下一手牌拿到完全相同的概率是 1/22100。所以答案是 (48/22100)*(1/22100) = 48/488410000,即 1/10,175,208。这比中 6/49 彩票的概率高出 1.37 倍,后者的概率是 1/13983816。
在一副 8 副牌的百家乐中,玩家和庄家在同一笔牌中同时获得一张 A 和一张方块 8 的概率是多少?
(8 2 /combin(416,2))* (7 2 /combin(414,2)) = 0.00000043,或 2308093 中的 1
我最近目睹了一件奇怪的事情。我当时正在观看一场五张牌的扑克游戏,最多只能抽两张牌。一位玩家抽了一张牌,凑成了红桃同花。庄家抽了一张牌,凑成了黑桃同花。当然,庄家的同花牌更大。游戏中还有另外三位玩家。同一手牌中出现两张同花的概率是多少?
让我们定义同花的概率,即在发牌时拿到一张牌,或者抽到四张同花。为了简单起见,我们假设玩家抽到一对或顺子,并且抽到四张同花。在发牌时拿到同花(不包括顺子/皇家同花)的概率是 4*(combin(13,5)-10)/combin(52,5) = 5108/2598960 = 0.0019654。拿到四张同花的概率是 4*3*combin(13,4)*13/combin(52,5) = 111540/2598960 = 0.0429172。抽到同花的概率是 9/47。因此,拿到四张同花并完成的总体概率为 0.0429172*(9/47) = 0.0082182。因此,拿到同花的总概率为 0.0019654 + 0.0082182 = 0.0101836。5 位玩家中恰好有 2 位拿到同花的概率为 combin(5,2) * 0.0101836 2 *(1-0.0101836) 3 = 0.001006,约为 1/994。
我想知道在五人玩一副牌的七张牌梭哈游戏中,有人拿到四张同花的概率是多少?希望您能帮助我,谢谢您的宝贵时间。
从 52 张牌中抽出 7 张,一共有 combin(52,7)=133,784,560 种排列方式。包含四张同点牌的 7 张牌组合的数量为 13*combin(48,3) = 224,848。13 表示四张同点牌的点数,combin(48,3) 表示从剩下的 48 张牌中抽出 3 张的排列方式数量。因此,概率为 224,848/133,784,560 = 0.0017,即 595 分之一。
当你打开一副新的牌时,每副牌的花色都是从A到K。将一副洗好的牌重新洗回原来的A到K状态,概率是多少?
52 阶乘中的 1,或 80,658,175,170,943,900,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000。
如果十个人从一副牌中每人得到两张牌,那么两个玩家拿到一对 A 的概率是多少?
首先,从 10 名玩家中选择 2 名玩家,共有 10*9/2=45 种方法。其中两名特定玩家拿到四张 A 的概率为 1/combin(52,4)=1/270725。因此,任意两名玩家拿到一对 A 的概率为 45/270725=0.0001662。
如果七名玩家每人拿到七张牌,那么至少有一人拿到 7 张同花牌的概率是多少?
单个玩家获得 7 张同花牌的概率为 4*combin(13,7)/combin(52,7) = 1/19491。7 个玩家中至少有一名玩家获得 7 张同花牌的概率约为 2785 分之一。
我知道从数学上来说一切皆有可能,但前几天晚上在赌场,我好像目睹了十亿分之一概率的事情,当然,这种事也并非从未发生过。事情是这样的:在“放马过来”的赌桌上,40手牌(40张单张三张牌,大约8轮,5人参与)中,有3张四条。四条的概率大约是4100比1,那么在40手牌中出现三张四条的概率是多少?请回答,这简直要把我逼疯了。我是老粉丝了。
为简单起见,我们假设每手牌都是从一副新牌中发出的。四条的概率是 13*48/combin(52,5) = 624/2598960。40 张四条中恰好出现 3 张的概率是 combin(40,3)*p 3 *(1-p) 37 = 1/7378135,其中 p = 624/2598960。所以这更像是七百万分之一的概率。
首先,我想告诉你,我非常喜欢你的网站,也非常钦佩你的数学能力。我用6副牌来发21点,还加了3张百搭牌,原因我就不多说了,不过,连续发3张百搭牌给一个玩家的概率是多少?非常感谢。
不客气,谢谢你的赞美。从六副牌的牌盒中连续发出三张百搭牌(加上三张百搭牌)的概率是 1/combin(315,3) = 1/5,159,805。另一个解是 (3/315)*(2/314)*(1/313)。
用一副52张的牌,给四个玩家每人发13张牌,四个玩家都拿到了从A到2的顺子,那么这四个玩家的概率是多少?这些牌不必是同一花色。
答案是 (4 13 /COMBIN(52,13))* (3 13 /COMBIN(39,13))* (2 13 /COMBIN(26,13)) = 1/61,204,166,001。
发到四张皇家牌的概率是多少?
皇家牌有四种可能的花色。有五张牌可能缺失。第五张牌可能是其他47张牌中的一张。因此,皇家牌共有4*5*47=940种组合方式。组合方式共有(52,5) = 2,598,960种。因此,概率为940/2,598,960 = 2,765分之一。
亲爱的小伙子,假设洗了一副52张牌,我们随机抽取18张,分成6堆,每堆3张。请问其中一堆恰好包含3张(4张中的3张)A的概率是多少?
解决这个问题的简单方法是,第一堆牌中有三张 A 的概率是 (4/52)*(3/51)*(2/50) = 1/5525。然而,每堆牌中有三张 A 的概率相同,所以我们乘以 6,得到 6/5525 = 0.001086
在五张牌梭哈游戏中拿到所有面牌的概率是多少?
(12/52)*(11/51)*(10/50)*(9/49)*(8/48) = 0.00030474,或约 3282 分之 1。
在玩 Let it Ride 游戏的两个小时内获得两张四条的概率是多少?
任何一手牌中出现四条的概率为 13*48/combin(52,5) = 0.0002401。假设你在两小时内可以玩 120 手牌。那么恰好出现两张四条的概率为:combin(120,2) × 0.0002401 (2 × (1-0.0002401) 118 = 0.000400095 = 1/2499.41。
在四张牌扑克中,顺子和同花哪个更有可能?
不算同花顺和皇家同花顺,顺子的概率是1.02%,同花的概率是1.04%。所以同花的概率略高一些。
在100万手牌中,出现20万手大同花顺荒的概率是多少?我对答案本身更感兴趣。
我很少这么说,但我试了好几个小时,但这个问题的数学计算实在太难了。所以我向我的朋友、数学教授加博尔·梅杰西(Gabor Megyesi)求助。这是他解决任何“干旱”问题的公式。
- 设 p 为赢得任何一手牌的概率。
- 设 d 为干旱持续时间。
- 设 n 为玩过的牌数。
- 设 k=dp 且 x=np。
- 如果 k=1,则令 a=-1,否则求 a 使得 k=-ln(-a)/(1+a)。(a 为负数,如果 k>1,则 -1 < a < 0,如果 k < 1,则 a < -1,且 a 需要高精度计算。)[向导注:此类解法可在 Excel 中使用工具菜单下的“目标求解”功能轻松找到。]
- 如果 k=1 则令 A=2,否则令 A=(1+a)/(1+ak)。
- n 年间不发生长度为 d 的干旱的概率约为 Ae a x 。
在这个特定问题中,p=1/40391,d=200000,n=1000000,k=4.9516,x=24.758,a=-0.0073337,A=1.03007。因此,不发生干旱的概率为 1.03007*e -0.0073337*24.758 = 0.859042。因此,至少发生一次干旱的概率为 1-0.859042 = 0.140958。
这是 Gabor Megyesi 的完整5 页解决方案(PDF)。感谢 Gábor 的帮助。
我随机模拟了32095组一百万手牌,其中至少出现一次干旱的号码是4558,概率为14.20%。
假设你从不同的牌堆中发出两手五张牌的扑克牌。你被告知A手牌至少包含一张A。你被告知B手牌包含一张黑桃A。哪一手牌更有可能包含至少一张A?
下表显示了完全随机的一手牌中出现 0 到 4 张 A 的概率。
Ace 概率 — 随机手牌
| 王牌 | 公式 | 组合 | 可能性 |
|---|---|---|---|
| 0 | 合并(48,5) | 1712304 | 0.658842 |
| 1 | 组合(4,1)×组合(48,4) | 778320 | 0.299474 |
| 2 | 组合(4,2)×组合(48,3) | 103776 | 0.03993 |
| 3 | 组合(4,3)×组合(48,2) | 4512 | 0.001736 |
| 4 | 组合(4,4)×组合(48,1) | 四十八 | 0.000018 |
| 全部的 | 2598960 | 1 |
对 1 到 4 张 A 牌进行求和,我们发现至少出现一张 A 牌的概率为 0.341158。出现两张或两张以上 A 牌的概率为 0.041684。
假设至少有一张 A,那么再出现一张 A 的概率可以用贝叶斯定理重新表述为概率(至少有一张 A 的情况下再出现两张 A)= 概率(两张或更多张 A)/概率(至少有一张 A)= 0.041684/ 0.341158 = 0.122185。
对于那些不熟悉贝叶斯定理的人来说,它指出给定 B 时 A 的概率等于 A 和 B 的概率除以 B 的概率,或者 Pr(A 给定 B) = Pr(A 和 B)/Pr(B)。
下表显示了从牌堆中移除黑桃 A 后,其他 A 的每个数量的组合和概率。
A 概率 — 移除 A 牌
| 王牌 | 公式 | 组合 | 可能性 |
|---|---|---|---|
| 0 | 组合(3,0)×组合(48,4) | 194580 | 0.778631 |
| 1 | 组合(3,1)×组合(48,3) | 51888 | 0.207635 |
| 2 | 组合(3,2)×组合(48,2) | 3384 | 0.013541 |
| 3 | 组合(3,3)×组合(48,1) | 四十八 | 0.000192 |
| 全部的 | 249900 | 1 |
这表明至少再出现一张 A 的概率为 0.221369。
为了好玩,让我们用贝叶斯定理来解答同样的问题。假设随机发牌,直到找到一手包含黑桃 A 的牌。假设牌中包含黑桃 A,那么至少再出现一张 A 的概率可以改写为概率(假设手中有黑桃 A,则至少有两张 A)。根据贝叶斯定理,这等于概率(手中有黑桃 A 且至少还有一张 A)/概率(手中有黑桃 A)。我们可以将分子分解为概率(包括黑桃 A 在内的 2 张 A)+概率(包括黑桃 A 在内的 3 张 A)+概率(4 张 A)。使用第一个表格,这等于 0.039930×(2/4) + 0.001736×(3/4) + 0.000018 = 0.021285。出现黑桃A的概率为5/52 = 0.096154。因此,给定黑桃A,至少出现两张A的概率为0.021285/0.096154 = 0.221369。
因此,如果至少有一张 A,则出现两张或两张以上 A 的概率为 12.22%,如果是黑桃 A,则出现两张或两张以上 A 的概率为 22.14%。
好吧,我相信你的数字,但这对我来说仍然说不通。我认为概率应该是相等的。你拿到一张A牌,花色有什么区别?
让我们看另一个更简单的情况。假设女性A说:“我有两个孩子,至少有一个是男孩。” 女性B说:“我有两个孩子,大一点的叫约翰。” 我们可以假设没有一个叫约翰的女孩,也没有女性会给多个孩子取同一个名字。使用条件概率,女性A的两个孩子都是男孩的概率是pr(两个男孩)/pr(至少一个男孩)= pr(两个男孩)/(1-pr(两个女孩))= (1/4)/(1-(1/4)) = (1/4)/(3/4) = 1/3。然而,女性B的较小孩子是男孩或两个孩子都是男孩的概率是?,因为说大孩子叫约翰并不能告诉我们关于较小孩子的任何信息。
再举一个例子,假设你去捷飞络 (Jiffy Lube),他们以相同的价格提供两种方案。方案 A 是他们会检查四个零件,只更换第一个发现的缺陷零件。方案 B 是他们只检查一个问题,如果发现问题就会修复。你难道不想选择方案 A 吗?你的车进来时预计有相同数量的坏零件,但在方案 A 下发现问题的概率更大,因此在方案 A 下你离开时预计会有少量缺陷零件。同样,测试任何 A 都可能出现唯一的 A,而测试黑桃 A 时不会检查其他三种花色,因此它们更有可能是 A。
在四张牌扑克中,如何使用 5 张牌中的 4 张牌得出同花顺的数量 2072?
首先,我将同花顺分为两种:四张连续同花色的牌和五张连续同花色的牌。五张同花顺的数量等于花色数 * 跨度数(A 到 10 为最低牌)= 4*10 = 40。对于四张同花顺,有 11 种不同的跨度(A 到 J 为最低牌)。对于 A234 和 JQKA 同花顺,第五张牌可以是 47 张牌中的一张(52 张牌减去已经取出的 4 张牌和可以组成五张同花顺的第五张牌,这四张牌已经计算在内)。因此,跨度为 A234 或 JQKA 的同花顺共有 4*2*47=376 张。对于其他九张牌,第五张牌有 46 种可能的牌(52 张牌减去已经取出的 4 张牌和可以组成五张同花顺的两张牌)。因此,跨度为 2345 到 TJQK 的同花顺数量为 4*9*46=1656。因此,4张同花顺的总数为40+376+1656=2072。
无论发出第17张牌是什么,同花的概率都是100%。那么,什么时候发出第几张牌,顺子概率是100%呢?
只有45张牌才能保证顺子。例如,即使你发了A、2、3、4、6、7、8、9、JQ和K,总共44张牌,你仍然无法凑成顺子。
尊敬的“概率奇才”先生,我对您的统计敏锐度赞叹不已。您能否帮我计算一下七张牌顺子的概率?例如,七张牌梭哈中出现 A、2、3、4、5、6、7,或者 2、3、4、5、6、7、8,或者 7、8、9、10、J、Q、K。我们知道这不是真正的扑克牌型;然而,我们在玩牌时碰巧碰到了它,我们想知道它的概率是否比七张牌梭哈中出现葫芦的概率更低。谢谢,您真是个博学之人。
你这么奉承我,我怎么能拒绝呢?首先,从 52 张牌中随机抽取 7 张牌,不考虑顺序,一共有(52,7) = 133,784,560 种组合方式。七张牌的顺子有 8 种可能的组合范围(最小的牌可能是 A 到 8)。如果牌型有 7 种不同的大小,那么花色就有47 = 16384 种排列方式。注意,这包括所有相同花色的牌,这样就能组成同花顺。所以概率是 8*16,384/133,784,560 = 1/1020.6952。
如果我从一副牌中发出 4 张牌,其中至少有 1 张牌是黑桃的概率是多少?
零张黑桃的概率为 (39/52)*(38/51)*(37/50)*(36/49) = 0.303818。因此,至少出现一张黑桃的概率为 1-0.303818 = 0.696182。
在一副牌的游戏中,四张牌中至少出现一张A和一张2的概率是多少?了解这一点对于奥马哈游戏来说很有用。
从概率101可知,Pr(A或B) = Pr(A) + Pr(B) - Pr(A和B)。因此,Pr(A和B) = Pr(A) + Pr(B) - Pr(A或B)。假设A拿到一张A,B拿到一张2。Pr(A) = Pr(至少一张A) = 1-Pr(没有A) = 1-combin(48,4)/ combin (52,4) = 1-0.7187 = 0.2813。没有2的概率显然相同。按照同样的逻辑,pr(A或B) = Pr(至少一张A或2) = 1-Pr(没有A也没有2) = 1-combin(44,4)/combin(52,4) = 1 - 0.501435 = 0.498565。因此,获得至少一张 A 和一张 2 的概率是 0.2813 + 0.2813 - 0.498565 = 0.063962。
在六张牌的游戏中连续 27 手拿到方块 J 的概率是多少?
任意一手拿到它的概率是 6/52。连续 27 手拿到它的概率是 (6/52) 27 = 20,989,713,842,161,800,000,000,000 分之一。
获得“死人之手”,即两对 A 和 8 的概率是多少?
每对牌有六种组合方式,可以从四种花色中抽出两种。单张牌有 44 张。因此,成功组合数为 6*6*44 = 1584。总共有 2,598,960 种组合方式,概率为 0.0609%。
我知道您已经回答过, 2005 年 4 月 3 日,拿到“死人之手”(两对 A 和 8)的概率是 0.0609%,但我相信死人之手是“两张黑 A、两张黑 8 和一张梅花 Q”,那么从一副标准牌中抽出这手牌的概率是多少?
只有一种方法可以拿到那一手牌。所以概率是 1/combin(52,5),也就是 2,598,960 分之一。
在一副标准的52张牌中,如果一张牌的花色相同,且不重复,那么每种可能的五张牌型的概率是多少?例如,假设这手牌是A♠ A♣ A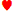 一个
一个 2. 在这手牌中,2 的花色不予考虑,可以代表牌堆中任意四张 2。另一个例子是 AJ-8-6-5。在这手牌中,所有 5 张牌的花色都不予考虑,因此只有一种这样的组合。另一个例子是:3♠ 3
2. 在这手牌中,2 的花色不予考虑,可以代表牌堆中任意四张 2。另一个例子是 AJ-8-6-5。在这手牌中,所有 5 张牌的花色都不予考虑,因此只有一种这样的组合。另一个例子是:3♠ 3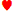 7♣ 7♠ Q。在这手牌中,两张3和两张4的花色不会被忽略,因为手中有不止一张3,但Q的花色是通用的。换句话说,任何牌中没有重复的牌的花色都会被忽略,并且该手牌被视为可能的手牌之一,即使如果不忽略每张牌的花色,该手牌再次出现的可能性会有很多。因此,由五张特定牌组成的顺子或同花,例如Q
7♣ 7♠ Q。在这手牌中,两张3和两张4的花色不会被忽略,因为手中有不止一张3,但Q的花色是通用的。换句话说,任何牌中没有重复的牌的花色都会被忽略,并且该手牌被视为可能的手牌之一,即使如果不忽略每张牌的花色,该手牌再次出现的可能性会有很多。因此,由五张特定牌组成的顺子或同花,例如Q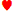 J♣ 10
J♣ 10 9
9 8♠ 或 A♠ J♠ 8♠ 7♠ 3♠ 只能出现一次,因为这些牌的任何其他组合,即使花色不同,也都属于重复。因此,根据这个标准,任何一手牌的胜率是多少?换句话说,在一副标准的52张牌的牌组中,有多少种这样的五张牌?感谢您的意见。
8♠ 或 A♠ J♠ 8♠ 7♠ 3♠ 只能出现一次,因为这些牌的任何其他组合,即使花色不同,也都属于重复。因此,根据这个标准,任何一手牌的胜率是多少?换句话说,在一副标准的52张牌的牌组中,有多少种这样的五张牌?感谢您的意见。
我对这个概念非常熟悉。五张牌共有134,459种不同的牌型。我之所以知道这一点,是因为我的第一个视频扑克程序分析了所有2,598,960种可能的牌型,并花了好几天才跑完一张赔率表。然而,如果只运行这134,459种牌型中的一种,并根据该类别中所有牌型的数量进行加权,就可以将运行时间缩短95%。有时,如果游戏的花色是特定的,比如我最近分析的“黑杰克红利扑克” ,我就不得不重新启用我的旧程序,用慢节奏的方式运行。
在玩五张牌梭哈时,如果使用 5 种花色而不是 4 种花色的牌,那么获胜的概率是多少?
五花扑克中的组合
| 手 | 组合 | 可能性 | 公式 |
| 五张相同的牌 | 十三 | 0.000002 | 十三 |
| 同花顺 | 50 | 0.000006 | 5*10 |
| 四条 | 3900 | 0.000472 | 13*12*组合(5,4)*5 |
| 冲洗 | 6385 | 0.000773 | 5*(组合(13,5)-10) |
| 客满 | 15600 | 0.001889 | 13*12*组合(5,3)*组合(5,2) |
| 直的 | 31200 | 0.003777 | 10*(5^5-5) |
| 三条 | 214500 | 0.025969 | 13*组合(12,2)*组合(5,3)*5^2 |
| 两对 | 429000 | 0.051938 | 组合(13,2)*11*组合(5,2)^2*5 |
| 一对 | 3575000 | 0.432815 | 13*组合(12,3)*组合(5,3)*5^3 |
| 没有什么 | 3984240 | 0.48236 | (组合(13,5)-10)*(5^5-5) |
| 全部的 | 8259888 | 1 |
请注意,我颠倒了葫芦和同花的顺序。
一副标准扑克牌中,有多少种五张牌的组合是由两种花色的牌组成的?
两种花色可以分成 4 和 1 或 3 和 2。我们先来看看 4/1 分割的情况。对于有 4 张牌的牌,有 4 种花色可供选择;对于有 1 张牌的牌,剩下 3 种花色可供选择。从 13 种花色中选择 4 种花色,共有 combin(13,4)=715 种方法。选择一个花色则有 13 种方法。因此,两种花色 4/1 分割的方式有 4×3×715×13=111,540 种。按照类似的逻辑,3/2 分割的方式有 4×3×combin(13,3)×combin(13,2)=267,696 种。因此,总概率为 (111540+267696)/combin(52,5) = 14.59%。
拿到2-3-4-5-7非同花的赔率是多少?非常感谢,这个网站太棒了!
谢谢。(4 5 -4)/combin(52,5)= 1020/2598960 = 2,548 中的 1。
前几天我在福克斯伍兹赌场观看福克斯伍兹扑克经典赛的最后两桌比赛。世界扑克巡回赛主持人之一文斯·范·帕滕(Vince Van Patten)进来观看比赛时,开始和一些在场的扑克高手进行各种赌注。他开价20比1,条件是参赛者能翻开一整副牌,牌面大小依次循环,并一边翻开一边大声念出A、2、3、4等等直到K的牌,然后从A重新开始,且不翻出他们要宣布的牌。没有人能翻完,文斯在大约10分钟内赢了几百美元,之后所有人都放弃了。我知道这肯定是可能的,但我怀疑文斯在开20比1的赔率时有点儿卖力。那么,真正翻开整副牌的几率有多大呢?
估算获胜概率的一个简单方法是假设每张牌都有12/13的概率不匹配指定的点数。为了赢得这场赌注,受害者必须成功下注52次。52次获胜的概率是(12/13) /52=1.56% 。合理的赔率是63.2比1。在20比1的赔率下,文斯的优势是67.3%(哎哟!)。
根据数学能力比我强的GM的说法,实际概率是1.6232727%。造成这种差异的原因是,每次选择的结果都与之前的选择呈正相关。
昨晚玩的时候,一位老玩家,一个老谋深算、脾气暴躁、喜欢在翻牌圈下等额的边注。这位老顽固赌徒押注翻牌圈的三张牌中会有一张是A、2或J(有时他会把这三张可识别的牌换掉)。这个赌注的赔率是多少?非常感谢您的智慧。
在翻牌圈未出现任何牌型的情况下,任意三个点数不出现在翻牌圈的概率为: combin (40,3)/combin(52,3) = 9880/22100 = 44.71%。所以这名玩家的优势是 10.59%。
假设从一副52张牌的牌堆中发出五张牌,第一张是K。至少还有一张K的概率是多少?我看到你做过一道和这个类似的Ace题,但我不太明白。谢谢你的帮助。
我更喜欢用组合函数来回答概率问题。这样一来,从一副牌中的48张非K牌中,选出四张非K牌的方法有(48,4) = 194,580种。从剩下的51张牌中,选出任意四张牌的方法有(51,4) = 249,900种。因此,接下来四张牌中没有K的概率是194,580/249,900 = 77.86%。因此,至少选出一种K的概率是100% - 77.86% = 22.14%。
有些人说,组合函数可能超出了问这类简单概率问题的人的理解范围。我并不反对这种说法,但创建这个网站的主要原因是想教我的读者一些数学知识。组合函数在概率论中非常有用,可以节省大量时间。然而,即使没有它,我们手头的问题也很容易回答。
第二张牌不是K的概率是48/51。这是因为牌堆里还剩下48张非K牌,而牌堆里总共剩下51张牌。如果第二张牌不是K,那么第三张牌也不是K的概率就是47/50(47张非K牌除以剩余的50张牌)。如此类推,其他四张牌都不是K的概率是(48/51)×(47/50)×(46/49)×(45/48) = 77.86%。其他四张牌都不是K的概率,换句话说,至少有一张K的概率是100% - 77.86% = 22.14%。
首先,从一副52张牌的牌堆中选出5张牌。然后,将它们的黑杰克点数(T、J、Q、K = 10,A = 1)相加。结果奇数/偶数的概率是多少?我认为,由于偶数牌数量过多,结果奇数的概率会更大。
令人惊讶的是,尽管52张牌中有30张是偶数,但奇数点数的可能性却高达50.03%。下表显示了奇数/偶数点数的概率。
奇数/偶数问题
| 埃文斯 | 赔率 | 组合 | 可能性 | 和 |
| 0 | 5 | 15504 | 0.005965 | 奇怪的 |
| 1 | 4 | 155040 | 0.059655 | 甚至 |
| 2 | 3 | 565440 | 0.217564 | 奇怪的 |
| 3 | 2 | 942400 | 0.362607 | 甚至 |
| 4 | 1 | 719200 | 0.276726 | 奇怪的 |
| 5 | 0 | 201376 | 0.077483 | 甚至 |
| 全部的 | 2598960 | 1 |
如果从一副牌中抽出三张牌,其中恰好有一张是黑桃,那么概率是多少?
第一张牌是黑桃,后两张不是的概率是 (13/52)×(39/51)×(38/50) = 14.53%。你应该将这个概率乘以 3,因为黑桃可能是三张牌中的任何一张。所以答案是 3×14.53% = 43.59%。对于喜欢使用组合函数的人来说,答案是 13×combin(39,2)/ combin (52,3) = 9,633/22,100 = 43.59%。
选择两个介于 0 和 1 之间的随机数(均匀分布)。现在选择其中较小的一个。选择的平均值是多少?n 个数字的一般情况呢?
对于两个数字,答案是 1/3;对于 n 个数字,答案是 1/(n+1)。我把答案发布到我的数学题页面,也就是第 194 题和第 195 题。
您正在玩一个包含三个人的游戏:(a) 您自己,(b) 您的对手,以及 (c) 一名裁判。你们每人秘密选择一个介于 0 到 1 之间的实数。所有数字都选好后,它们就会被揭晓。猜得最接近裁判数字且不超过的玩家获胜。如果您猜得更接近,您将赢得 1 美元。如果您的对手猜得更接近,您将输掉 1 美元。如果双方都猜得超过或出现平局,则游戏为平局。
如果对方随机选择,你能否选择一个数字,使你的预期回报最大化?如果对方也有策略呢?
希望你满意,我花了一整天时间做第二部分,但答案还是错的。为了避免让读者失去同样的乐趣,我不会在这里直接说出答案。我把这个问题分成了两个问题,并在mathproblems.info上发布了答案和解答,分别是问题 196 和 197。
如果从标准的 52 张牌中随机抽取五张牌,那么四种花色都出现的概率是多少?
必须有一种花色包含两张牌,还有三种花色,每张牌包含一张牌。出现两次的花色有四种可能的花色。对于出现两次的花色,有 (13,2)=78 种组合方式可以从 13 种花色中选择 2 种。对于其他三种花色,每种花色都有 13 种可能的花色。因此,总组合数为 4 × 78 × 13 × 13 × 13 = 685,464。从 52 张牌中选择 5 张牌,有 (52,5)=2,598,960 种组合方式。因此,概率为 685,464/2,598,960 = 26.37%。
任意两个选定的牌型,比如皇后和国王,在一副随机的牌中连续出现的概率是多少?有人跟我挑战,要我跟他打个等额的赌,赌这件事会发生。
根据随机模拟,概率是48.64%。所以,我会接受这个赌注。
您能否推荐一个函数,将 52 张牌中的任意五张牌映射到 0 到 2,598,959 之间的整数?
是的。首先给每张卡片分配一个从 0 到 51 的值。将卡片命名为 c1 到 c5,并按 c1 为最低、c5 为最高的顺序排列。然后调用以下函数:
int GetIndex(int c1,int c2,int c3,int c4,int c5)
{
返回组合(c5,5) + 组合(c4,4)+ 组合(c3,3) + 组合(c2,2) + 组合(c1,1);
}
其中,combin 返回传统值,但如果第一个值小于第二个值,则返回 0,如下所示:
int 组合(int x,int y)
{
如果(y>x)
返回 0;
别的
{
int i,n;
n=1;
对于(i = x-y + 1;i <= x;i ++)
n*=i;
对于(i=2;i<=y;i++)
n/=i;
返回 n;
}
}
如果您这样做是为了访问数组元素,请按如下方式加载数组。
计数=0;
对于(c5 = 4;c5 < 52;c5 ++)
{
对于(c4 = 3;c4 < c5;c4++)
{
对于(c3 = 2;c3 < c4;c3++)
{
对于(c2 = 1;c2 < c3;c2++)
{
对于(c1 = 0;c1 < c2;c1 ++)
{
index_array[count]=无论你想要什么;
计数++;
}
}
}
}
}
从 10 张同花顺中抽出 3 张,持有 3 张同花顺且有 1 张缺口的概率是多少?

这是一个二项分布问题。其一般公式是:如果某个事件的概率为 p,且每个结果都是独立的,那么该事件在 t 次试验中恰好发生 w 次的概率为(t,w)×p w ×(1-p) tw 。
在这种情况下,有两种方法可以组成同花顺。你需要一张方块8和另一张方块6或J。从牌堆剩下的47张牌中抽出2张,一共有combin(47,2)=1,081种方法。因此,任何一手牌中抽出同花顺的概率是2/1,081 = 0.0018501。10张牌中抽出3张的概率是combin(10,3)×0.0018501 3 ×(1-0.0018501) 7 = 0.000000750178,即1/1,333,017。
将两副54张牌(包括两张鬼牌)洗在一起。给一位玩家一半。这位玩家拿到全部四张红色3的概率是多少?
有 4 张红色 3 和 104 张其他牌。只有一种方法可以凑齐所有 4 张红色 3。玩家有 (104,50)= 1.46691 × 10 28种组合方式可以凑齐另外 104 张牌中的 50 张。总组合数为 (108,54)= 2.48578 × 10 30 。组合数 (104,50)/组合数 (108,54) = 0.059012。
如果您不喜欢处理如此大的数字,这里有一个替代解决方案。将四个红色三号按 1 到 4 进行编号。第一个红色三号在玩家牌堆中的概率是 54/108。现在移除前三个。玩家拥有第二个红色三号的概率是 53/107,因为玩家剩余 53 张牌,而牌堆里还有 107 张。同样,玩家拥有第三个红色三号的概率是 52/106,第四个红色三号的概率是 51/105。(54/108) × (53/107) × (52/106) × (51/105) = 0.059012。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
您在2010年12月14日的专栏中写道,赌场特别提到的“AAAAAKK”牌型在扑克历史上可能从未出现过。据另一位荷官说,一位玩家在2010年11月在主街车站(Main Street Station)拿到了这手牌。
有意思。我之前写过,我估计内华达州每23.7年就会出现一次这种手。我想那次就是其中一次。
假设你选择两个等级,例如国王和王后。在一副随机洗好的52张牌中,国王和王后至少出现一次相邻的概率是多少?
我的概率是48.6279%。如果你想下注的话,“是”的合理赔率是1.0564比1。
我听说最近有一场“完美”的桥牌比赛,每位玩家都拿到了四种花色之一的13张牌。这样的概率是多少?
也有传言称,2011 年在沃里克郡举行的一场惠斯特牌局中也发生过类似的事情。为了方便其他读者,我想问的是,将一副 52 张牌的扑克牌分成四组,每组 13 张,每组完全由某一花色的 13 张牌组成的概率是多少。
将 52 张牌分成四组,每组 13 张,一共有 combin(52,13)combin(39,13)*combin(26,13) = 53,644,737,765,488,800,000,000,000,000 种可能的方式。4! = 24 是获胜组合数,因为您可以按照自己希望的方式将四种花色分配给四位玩家。因此,获胜几率等于 2,235,197,406,895,370,000,000,000,000 分之一。为了更直观地理解这个数字,假设地球上 75 亿人以每秒一次的速度打桥牌,那么在 50 亿年后太阳爆炸之前,有人发出所谓完美牌型的概率是 16,558 分之一。
然而,有些人将“完美”牌型定义为一位玩家拿到任意花色的全部13张牌。我指出,这种情况发生的概率是39,688,347,497场游戏中的1分之一。这种情况在地球上的某个地方可能偶尔会发生。
在德州扑克游戏中,两名玩家同时使用两张底牌拿到同花的概率是多少?
首先,让我们确定可能发生这种情况的玩家牌和公共牌的组合数。显然有四种花色。那么,从给定花色的 13 张牌中选出 4 张,一共有 combin(13,4)=715 种组合方式。
其次,一种可能发生这种情况的方式是,玩家在牌桌上有三张相同花色的牌,另外两张在另外39张牌中。牌桌上有三张相同花色的牌,组合方式有(9,3)=84种。然后,有组合方式有(39,2)=741种,可以从另外三种花色的39张牌中再选出两张。因此,牌桌上有三张相同花色的牌,组合方式有84*741=62,244种。
第三,另一种可能发生这种情况的方式是,玩家在公共牌上有四张相同花色的牌,另一张在另外 39 张牌中。公共牌上有所选花色剩余 9 张牌中的 4 张,共有 combin(9,4)=126 种方法。然后,有 39 种方法可以从其他三种花色的另外 39 张牌中再选一张。然而,并非所有这些方法都会导致两位玩家都使用两张底牌。要满足该条件,公共牌上必须有该花色的最小牌。在 8 张该花色的牌中,出现这种情况的概率是 4/8 = 1/2。因此,公共牌上有四张该花色的牌共有 126*39*(1/2)=2,457 种方法。
第四,最后一种情况是,玩家手中持有五张相同花色的牌。共有 combin(9,5)=126 种组合方式,即牌桌上有五张相同花色的牌。然而,并非所有组合方式都会导致两位玩家都使用两张底牌。要满足该条件,牌桌上必须有该花色的最小两张牌。在当前牌桌上有九张相同花色的牌中,出现这种情况的概率为 combin(5,2)/combin(9,2) = 10/36 = 5/18。因此,共有 126*(5/18)=35 种组合方式,即牌桌上有四张相同花色的牌。
因此,发生这种情况的组合数为 715*(62,244 + 2,457 + 35) = 46,286,240。
从 52 张牌中挑选 4 张作为玩家底牌,然后从牌面上剩余的 48 张牌中挑选 5 张作为玩家底牌,总组合数为 combin(52,4)*combin(48,5) = 463,563,500,400。
因此,概率为 46,286,240 / 463,563,500,400 = 0.000399395 = 2,504 分之一。
这个问题是在我的Wizard of Vegas论坛中提出并讨论的。
一位赌场荷官正在研究一种新的三张牌扑克游戏。她从一副标准牌中取出所有人头牌,并彻底洗牌。然后,她给玩家1发了3张牌,给玩家2发了3张牌,给玩家3发了3张牌,最后给玩家4发了3张牌。四手牌中都包含顺子(任意花色的JQK)的概率是多少?
[剧透=解决方案]
每次发牌给一位玩家。第一位玩家拿到每种等级的牌的概率为 4^3/combin(12,3) = 64/220。
假设第一个玩家拿到顺子,那么牌堆里每个点数的牌就剩下三张了。第二个玩家拿到每个点数一张的概率是 3^3/combin(9,3) = 27/84。
假设前两位玩家拿到顺子,那么牌堆里每种点数的牌就剩下两张了。那么第三位玩家拿到每种点数各一张的概率是 2^3/combin(6,3) = 8/20。
假设前三名玩家拿到了顺子,那么牌堆里就剩下一张牌,每张牌都剩一张。这三张牌显然组成了顺子。
因此,四名玩家全部拿到顺子的概率为 (64/220)*(27/84)*(8/20)*1 = 216/5775 = 72/1925 = 3.74%。
[/spoiler]这个问题是在我在 Wizard of Vegas 的论坛上提出并讨论的,从这篇文章开始。
假设我有一副48张的牌,四种花色,每种花色12张。如果我抽15张牌,那么我抽到每种花色至少一张牌的概率是多少?
让我们从 100% 开始,减去导致少于四种花色的概率。
例如,48张牌中没有红桃的概率是多少?有36张牌不是红桃。从36张牌中选出15张的方法数为combin(36,15) = 5,567,902,560。从全部48张牌中选出15张的方法数为1,093,260,079,344。因此,15张牌中没有红桃的概率为5,567,902,560 / 1,093,260,079,344 = 0.005093。
接下来,让我们将其乘以四,得到缺少任何花色(而不仅仅是红心)的概率:4 × combin(36,15)/combin(48,15) = 0.02037174。
然而,这会导致某些情况重复计算。假设拿到 15 张黑牌。这样会忽略红桃和方块。这种情况就会重复计算。因此,我们需要进行修正。从四种花色中选择两种花色,共有 combin(4,2) = 6 种方法。所有 15 张牌都是任意两种特定花色的概率为 combin(24,15)/combin(48,15) = 1307504/1,093,260,079,344 = 0.00000120。如上所述,从四种花色中选择两种花色有六种方法,因此所有牌都是两种花色的方法数为 6 × combin(24,15)/combin(48,15) = 0.00000718。
减去重复计算的结果,我们得到出现两套或三套花色的概率为 0.02037174 - 0.00000718 = 0.02036456。
请注意,我们不需要担心一种花色的代表,因为不可能从 12 张牌中选择 15 张。
最后一步,从 100% 中减去 2 种或 3 种花色的概率,得到全部四种花色出现的概率:1.00000000 - 0.02037174 = 0.97963544。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
如果我从一副洗好的(假定是随机的)牌中发出 13 张牌,我应该看到多少种不同的等级?
如果存在的话,这就是马尔可夫链类型的问题。
下表显示了从 1 到 52 的所有牌张中,0 到 4 张牌的预期等级数。
根据发牌预测排名
| 牌 | 0 排名 | 1 级 | 2级 | 3个等级 | 4个等级 | 预期的 等级 |
|---|---|---|---|---|---|---|
| 1 | 12.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
| 2 | 11.058824 | 1.882353 | 0.058824 | 0.000000 | 0.000000 | 1.941176 |
| 3 | 10.174118 | 2.654118 | 0.169412 | 0.002353 | 0.000000 | 2.825882 |
| 4 | 9.343577 | 3.322161 | 0.324994 | 0.009220 | 0.000048 | 3.656423 |
| 5 | 8.564946 | 3.893157 | 0.519088 | 0.022569 | 0.000240 | 4.435054 |
| 6 | 7.836014 | 4.373589 | 0.745498 | 0.044178 | 0.000720 | 5.163986 |
| 7 | 7.154622 | 4.769748 | 0.998319 | 0.075630 | 0.001681 | 5.845378 |
| 8 | 6.518655 | 5.087731 | 1.271933 | 0.118319 | 0.003361 | 6.481345 |
| 9 | 5.926050 | 5.333445 | 1.561008 | 0.173445 | 0.006050 | 7.073950 |
| 10 | 5.374790 | 5.512605 | 1.860504 | 0.242017 | 0.010084 | 7.625210 |
| 11 | 4.862905 | 5.630732 | 2.165666 | 0.324850 | 0.015846 | 8.137095 |
| 12 | 4.388475 | 5.693157 | 2.472029 | 0.422569 | 0.023770 | 8.611525 |
| 十三 | 3.949628 | 5.705018 | 2.775414 | 0.535606 | 0.034334 | 9.050372 |
| 14 | 3.544538 | 5.671261 | 3.071933 | 0.664202 | 0.048067 | 9.455462 |
| 15 | 3.171429 | 5.596639 | 3.357983 | 0.808403 | 0.065546 | 9.828571 |
| 16 | 2.828571 | 5.485714 | 3.630252 | 0.968067 | 0.087395 | 10.171429 |
| 17 | 2.514286 | 5.342857 | 3.885714 | 1.142857 | 0.114286 | 10.485714 |
| 18 | 2.226939 | 5.172245 | 4.121633 | 1.332245 | 0.146939 | 10.773061 |
| 19 | 1.964946 | 4.977863 | 4.335558 | 1.535510 | 0.186122 | 11.035054 |
| 20 | 1.726771 | 4.763505 | 4.525330 | 1.751741 | 0.232653 | 11.273229 |
| 21 | 1.510924 | 4.532773 | 4.689076 | 1.979832 | 0.287395 | 11.489076 |
| 22 | 1.315966 | 4.289076 | 4.825210 | 2.218487 | 0.351261 | 11.684034 |
| 23 | 1.140504 | 4.035630 | 4.932437 | 2.466218 | 0.425210 | 11.859496 |
| 24 | 0.983193 | 3.775462 | 5.009748 | 2.721345 | 0.510252 | 12.016807 |
| 二十五 | 0.842737 | 3.511405 | 5.056423 | 2.981993 | 0.607443 | 12.157263 |
| 二十六 | 0.717887 | 3.246098 | 5.072029 | 3.246098 | 0.717887 | 12.282113 |
| 二十七 | 0.607443 | 2.981993 | 5.056423 | 3.511405 | 0.842737 | 12.392557 |
| 二十八 | 0.510252 | 2.721345 | 5.009748 | 3.775462 | 0.983193 | 12.489748 |
| 二十九 | 0.425210 | 2.466218 | 4.932437 | 4.035630 | 1.140504 | 12.574790 |
| 三十 | 0.351261 | 2.218487 | 4.825210 | 4.289076 | 1.315966 | 12.648739 |
| 31 | 0.287395 | 1.979832 | 4.689076 | 4.532773 | 1.510924 | 12.712605 |
| 三十二 | 0.232653 | 1.751741 | 4.525330 | 4.763505 | 1.726771 | 12.767347 |
| 33 | 0.186122 | 1.535510 | 4.335558 | 4.977863 | 1.964946 | 12.813878 |
| 三十四 | 0.146939 | 1.332245 | 4.121633 | 5.172245 | 2.226939 | 12.853061 |
| 三十五 | 0.114286 | 1.142857 | 3.885714 | 5.342857 | 2.514286 | 12.885714 |
| 三十六 | 0.087395 | 0.968067 | 3.630252 | 5.485714 | 2.828571 | 12.912605 |
| 三十七 | 0.065546 | 0.808403 | 3.357983 | 5.596639 | 3.171429 | 12.934454 |
| 三十八 | 0.048067 | 0.664202 | 3.071933 | 5.671261 | 3.544538 | 12.951933 |
| 三十九 | 0.034334 | 0.535606 | 2.775414 | 5.705018 | 3.949628 | 12.965666 |
| 40 | 0.023770 | 0.422569 | 2.472029 | 5.693157 | 4.388475 | 12.976230 |
| 41 | 0.015846 | 0.324850 | 2.165666 | 5.630732 | 4.862905 | 12.984154 |
| 四十二 | 0.010084 | 0.242017 | 1.860504 | 5.512605 | 5.374790 | 12.989916 |
| 43 | 0.006050 | 0.173445 | 1.561008 | 5.333445 | 5.926050 | 12.993950 |
| 四十四 | 0.003361 | 0.118319 | 1.271933 | 5.087731 | 6.518655 | 12.996639 |
| 45 | 0.001681 | 0.075630 | 0.998319 | 4.769748 | 7.154622 | 12.998319 |
| 46 | 0.000720 | 0.044178 | 0.745498 | 4.373589 | 7.836014 | 12.999280 |
| 四十七 | 0.000240 | 0.022569 | 0.519088 | 3.893157 | 8.564946 | 12.999760 |
| 四十八 | 0.000048 | 0.009220 | 0.324994 | 3.322161 | 9.343577 | 12.999952 |
| 49 | 0.000000 | 0.002353 | 0.169412 | 2.654118 | 10.174118 | 13.000000 |
| 50 | 0.000000 | 0.000000 | 0.058824 | 1.882353 | 11.058824 | 13.000000 |
| 51 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 12.000000 | 13.000000 |
| 52 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 13.000000 | 13.000000 |
我在Wizard of Vegas论坛上提出并讨论了这个问题。
有人向我挑战,要我进行以下赌注。我可以从一副标准扑克牌中选择任意三个点数,写下我的预测,但要保密到最后。例如,7-A-2。然后他提出和我打等额赌注,如果他猜对三次,他至少能猜出我的一个点数。我赢的几率是多少?
要想获胜,对手的三次预测都必须全部错误。第一次预测有 10/13 的概率是错误的。第二次预测有 9/12 的概率是错误的,因为我们可以排除第一个猜测的排名的可能性。第三次预测有 8/11 的概率是错误的,因为我们可以排除前两个猜测的排名的可能性。
这三件事必须同时发生,你才能获胜。因此,你获胜的概率是 (10/13) * (9/12) * (8/11) = 720/1716 = 41.96%。
在均等赌注下,从您的角度来看,这场赌注的庄家优势是 16.08%(哎哟!)。
这个问题摘自欧文·埃谢 (Owen E'Shea) 所著的《命题赌注之书》(第 7 期)。
有人跟我打赌,说他能在27次掷骰子中用两个骰子总共掷出12点。如果他没掷出,我就能赢12点。既然掷出12点的概率是1/36,那他平均要掷36次才能掷出12点吗?如果我的对手只掷了27次,那看来我的胜算就大了。我猜对了吗?还是我的计算有什么问题?
两次掷出 12 点的平均等待时间确实是 36 次,包括掷出 12 点本身。然而,这并不意味着它们每 36 次掷出一次。掷不出 12 点的概率是 (35/36)。27 次掷出 12 点的概率是 (35/36)^27。因此,至少掷出一次 12 点的概率是 1-(35/36)^27 = 53.26%。
下表显示了在20至36次投掷中至少掷出12的概率。注意,需要掷出25次才能在均等赔率下获得优势。
概率 12
| 面包卷 | 可能性 |
|---|---|
| 20 | 43.07% |
| 21 | 44.66% |
| 22 | 46.19% |
| 23 | 47.69% |
| 24 | 49.14% |
| 二十五 | 50.55% |
| 二十六 | 51.93% |
| 二十七 | 53.26% |
| 二十八 | 54.56% |
| 二十九 | 55.82% |
| 三十 | 57.05% |
| 31 | 58.24% |
| 三十二 | 59.40% |
| 33 | 60.53% |
| 三十四 | 61.63% |
| 三十五 | 62.69% |
| 三十六 | 63.73% |
我们知道,在 52 张牌中,五张牌共有 combin(52,5)=2,598,960 种可能的组合。我的问题是,从五副牌的牌盒中可以得到多少种可能的五张牌?
让我们一次讨论一种类型的手。
- 五张相同的牌:一副牌中有 52 张不同的牌,有 52 种组合。
- 四张同点牌:四张同点牌有 52 种可能,单张同点牌有 51 种可能。因此,四条共有 52*51 = 2,652 种可能的组合。
- 三张相同的牌,两张不同的牌:三张相同的牌有 52 种可能,一对有 51 种可能。因此,葫芦有 52*51 = 2,652 种可能的组合。
- 三张相同的牌和两张不同的单张牌:三张相同的牌有 52 种可能的组合,而两张单张牌的组合有 (51,2)=1,275 种可能的组合。因此,三条有 52*1,275 = 66,300 种可能的组合。
- 两对相同的牌和一张单张牌:两张不同的牌组成对子,一共有 (52,2)=1,326 种组合。单张牌还有 50 种组合。因此,两对牌共有 1,326*50=66,300 种可能的组合。
- 一对相同的牌和三张单张牌:该对牌共有 52 张可能的牌。那么,从剩下的 51 张单张牌中选择 3 张,组合方式共有 (51,3)=20,825 种。因此,一对牌的组合数为 52*20,825 = 1,082,900。
- 五个单例:从 52 张牌中选择 5 张牌共有 combin(52,5)=2,598,960 种方法。
所有这些组合的总和是 3,819,816。
我在Wizard of Vegas论坛上提出并讨论了这个问题。


