非赌场游戏 - 常问问题
我喜欢用美元玩“说谎者扑克”游戏。请问一张钞票上出现任意一个相同数字的概率是多少?谢谢。如果我和三个人一起玩,出现任意一个数字的概率是多少?
首先,让我来回答一个未被提及的问题:某个特定数字在一张随机钞票上出现 n 次的概率。一张钞票上有 8 位数字,因此特定数字出现 n 次的概率为 combin(8,n)*0.1 n *0.9 8-n /10 8 。下表显示了特定数字出现 0 到 8 次的概率。
骗子扑克中的特定数字赔率
| 数字 | 可能性 |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| 全部的 | 1.00000000 |
下表列出了每种可能出现的钞票类型的概率,按每种类型的数量分类。例如,序列号 66847680 的钞票可能出现一张三张同点钞票、一张对子钞票和三张单张钞票,概率为 0.1693440。
说谎者扑克中的一般概率
| 8 橡木 | 7 橡木 | 6 橡木 | 5 橡木 | 4 橡木 | 3 橡木 | 2 橡木 | 1 橡木 | 可能性 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0.0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0.0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0.3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| 全部的 | 1.0000000 | |||||||
橡木 = “一种”
欲了解更多信息,请参阅我的“骗子扑克”页面。
美国银行推出活动,每日在ATM机上选择一笔存款进行三倍奖励。活动持续约两个月。存入300美元...分三次各存100美元还是一次性存入300美元...中奖概率更高?还是整体中奖率太低,不值得费心?
无论你将总存款分成多少次,预期收益都是相同的。一个好的策略是尽可能多次地重复存取同一笔资金。不过,你的胜率可能太低,以至于不值得这么麻烦。
想问一下关于东方骰子游戏的问题。游戏中玩家需要猜测骰子的哪一面朝上。玩家首先在1、2、3、4、5、6上投注(类似轮盘赌),然后“庄家”会同时掷3个骰子。如果所选数字出现一次(在3个骰子中的任何一个上),赔率为1:1;如果所选数字出现两次,赔率为2:1;如果所选数字同时出现在3个骰子上,赔率为3:1。由于玩家可以任意下注,那么最佳下注数是多少?(假设我所有赌注的数额相同)
在 Windows 版本中赢得标准 Klondike Solitaire 游戏的几率是多少?
这大概是我最常被问到却又无法回答的问题了。至今为止,还没有人做过完整的克朗代克纸牌游戏。或许,等电脑速度提升一百万倍,最终会有人做到。不过,据说拉斯维加斯的赌场至少在五十年代就提供过这种游戏。我问过不少拉斯维加斯老玩家,想证实这一点,但至今无人能证实。
我最近在玩西洋双陆棋时,连续四次掷出双六。这种情况再次发生的概率是多少?
每次新掷骰子时,接下来四次掷骰子均为双六的概率为 (1/36) 4 = 1/1679616。
您好, www.transience.com.au/ pearl.html 上有一个叫做“猪猡珍珠”的游戏。珍珠被分成三行(5+4+3),轮到你时,你可以从一行中移除任意数量的珍珠。游戏的目标是把最后一颗珍珠留给对手。玩家(我)总是先手(也总是输)。为什么我总赢不了?我的对手有一个狡猾的策略,总能赢,你能揭穿他的秘密吗?
首先从3颗珍珠的那一行移除2颗珍珠,剩下1+4+5。无论对手在下一轮做什么,都留下以下任意一张:1+1+1、1+2+3或4+4。用其中任意一张珍珠,迫使对手的牌堆变成两堆,每堆2颗或以上,或者奇数堆,每堆1颗。
大富翁游戏中的哪一套最好?
我最喜欢橙色组合。它能带来最佳的投资回报率。例如,橙色组合中,酒店租金为 500 美元,平均租金为 966.67 美元,租金与费用比率为 1.93。唯一一个比率更高的组合是浅蓝色组合,为 2.27。然而,浅蓝色组合的最高租金只有 600 美元。橙色组合中三栋房屋的租金与浅蓝色组合中的酒店租金相同,但成本低 20%,而且还有扩建空间。此外,橙色组合非常适合刚出狱的年轻人。所以听我的建议,交易时尽量买橙色组合。
您对玩石头/剪刀/布有什么建议?
本站最好的建议可能是:第一轮,总是选布。这是因为业余玩家往往第一次就选石头。只要每次伸出手,一次一个,你就会发现石头是最舒服、最自然的选择。如果你重复玩几轮,你应该选择任何能在最后一轮击败对手的概率小于三分之一的牌。这是因为我相信业余玩家重复玩的次数不到三分之一。如果你与一个你担心会闯入你脑海的职业选手比赛,那么通过查看手表的秒针随机化,将秒数除以三取余数,然后将余数映射如下:0=石头,1=剪刀,2=布(或任何其他提前确定的映射)。所以下次你去荷兰式餐厅时,我建议你先玩一轮结账,然后再选布。你以后会感谢我的。
当攻击者掷出三个骰子而防御者掷出两个骰子时,谁在风险中占有优势?
对于那些不熟悉这款游戏的人来说,《Risk》是有史以来最伟大的桌游。没玩过的人还不算真正体验过。在常见的3对2战斗中,以下是可能的结果:
- 防守方两败俱伤:37.17%
- 各输一分:33.58%
- 攻击者两败俱伤:29.26%
在 Yahtzee 游戏中,如果卡片上只剩下 Yahtzee 本身,那么成功的可能性是多少?
下表根据您玩 Yahtzee 所需的额外骰子数量显示了最后一次掷骰子的成功概率。
最后掷骰子概率
| 需要 | 可能性 成功 |
| 0 | 1 |
| 1 | 0.166667 |
| 2 | 0.027778 |
| 3 | 0.00463 |
| 4 | 0.000772 |
下表显示了改进的概率。左列显示每次掷骰前需要掷出多少个骰子,上列显示每次掷骰后需要掷出多少个骰子。正文部分显示了达到给定改进程度的概率。
改进的可能性
| 滚动前需要 | 0 | 1 | 2 | 3 | 4 | 全部的 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0.166667 | 0.833333 | 0 | 0 | 0 | 1 |
| 2 | 0.027778 | 0.277778 | 0.694444 | 0 | 0 | 1 |
| 3 | 0.00463 | 0.069444 | 0.37037 | 0.555556 | 0 | 1 |
| 4 | 0.000772 | 0.01929 | 0.192901 | 0.694444 | 0.092593 | 1 |
下表显示了首次掷骰子时需要 0 到 4 个骰子才能掷出 Yahtzee 的概率。
首次掷骰子概率
| 需要 | 可能性 |
| 0 | 0.000772 |
| 1 | 0.019290 |
| 2 | 0.192901 |
| 3 | 0.694444 |
| 4 | 0.092593 |
下表显示了根据第一次掷骰子后所需掷骰子数,改进并最终成功的概率。例如,如果玩家需要再掷3个骰子才能完成Yahtzee游戏,那么第二次掷骰子后改进为再掷2个骰子并在第三次掷骰子时完成Yahtzee游戏的概率为0.010288066。
根据第二次掷骰子前后所需的数字,第一次掷骰子后 Yahtzee 的概率
| 滚动前需要 | 0 | 1 | 2 | 3 | 4 | 全部的 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0.166667 | 0.138889 | 0 | 0 | 0 | 0.305556 |
| 2 | 0.027778 | 0.046296 | 0.01929 | 0 | 0 | 0.093364 |
| 3 | 0.00463 | 0.011574 | 0.010288 | 0.002572 | 0 | 0.029064 |
| 4 | 0.000772 | 0.003215 | 0.005358 | 0.003215 | 0.000071 | 0.012631 |
要得到最终答案,请将前两张牌上掷出所需的数字与最后一列上掷出一张牌的最终成功概率相乘。结果为:0.092593*0.012631+0.694444*0.029064+0.192901*0.093364+0.019290*0.305556+0.000772*1=4.6028643%。为了验证这一点,我进行了1亿次游戏模拟,模拟的概率为4.60562%。
如果在石头/剪刀/布游戏中引入炸药作为选项,其中炸药击败石头和布,但剪刀击败炸药,那么如果两个完美的逻辑学家在玩,最佳策略应该是什么?
首先,我们可以排除出纸的可能性。无论对方出什么,你都可以通过用炸药盖住纸来获得相同或更好的结果。一旦纸被盖住,炸药就变成了新的纸,打败了石头,输给了剪刀。所以,完美的策略是在石头、剪刀和炸药之间随机选择,并且概率相同。
当你必须在有限的时间内收集尽可能多的钱时,在那些四处飘散的钱摊位中,最好的策略是什么?
我向Fun Industries Inc.的Randy Hill咨询了这个问题。他说你应该伸直手臂,手掌向下,让钱在你的手掌和手臂底部膨胀起来。等到钱攒够了,就把钱塞进投币口。
假设我们有一个赌博游戏。一枚无偏硬币被反复抛掷。每次抛掷,我们需要支付 1 卢比。结果有两种可能:H 或 T。如果抛出正面和反面的差值为 3,我们将从赌徒那里得到 8 卢比。我们应该玩这个游戏吗?为什么?我们获胜的概率是多少?当我们掷出 7 或 9 卢比时,什么因素会影响获胜的概率?
我们将 x 称为从起点开始的翻转预期次数。
如果其中一方的翻转次数占多数,则我们将 y 称为剩余翻转的预期次数。
如果一方的翻转次数占多数,则我们将 z 称为剩余翻转的预期次数。
E(x) = 1 + E(y)
E(y) = 1 + 0.5*E(x) + 0.5*E(z)
E(z) = 1 + 0.5*E(y)
由此,用矩阵代数很容易得出 E(x) = 9,E(y) = 8,E(z) = 5。因此,平均需要抛掷 9 次才能使正面和反面的概率差达到 3。因此,对于每次抛掷都能赢取 1 卢比的人来说,8 卢比的赌注是一个不错的选择,因为他平均能赢 9 卢比,但只损失 8 卢比。对于赌徒来说,赌场优势是 11.11%。9 卢比的赌注是公平的,7 卢比的赌注则为 22.22%。
您在2002年11月28日的专栏中讨论了《Pearls Before Swine》这款游戏的正确策略。这款游戏还有续作《Pearls Before Swine II》 。我该如何通关这个版本呢?
我在2002年11月28日那一栏解释了当只剩下三行时该如何玩。以下是我的四行策略。轮到你时,查看左栏的排列,然后根据右栏的排列进行游戏。例如,起始位置3456列在最后,这表明你应该从有5颗珍珠的那一行中移除4颗,剩下1346颗。如果左栏显示“输”,即使对手采取最优策略,你也绝对不可能获胜,而Transcience的游戏似乎总是如此。
这张表的一个规律似乎是,你应该迫使对手陷入这样一种境地:最小行和最大行的珍珠总数等于中间两行的珍珠总数。这就意味着珍珠数量最少的那一行留零。
明珠暗投 II 策略
| 你有 | 离开 |
| 1111 | 111 |
| 1112 | 111 |
| 1113 | 111 |
| 1114 | 111 |
| 1115 | 111 |
| 1116 | 111 |
| 1122 | 失去 |
| 1123 | 1122 |
| 1124 | 1122 |
| 1125 | 1122 |
| 1126 | 1122 |
| 1133 | 失去 |
| 1134 | 1133 |
| 1135 | 1133 |
| 1136 | 1133 |
| 1144 | 失去 |
| 1145 | 1144 |
| 1146 | 1144 |
| 1155 | 失去 |
| 1156 | 1155 |
| 1222 | 1122 |
| 1223 | 1122 |
| 1224 | 1122 |
| 1225 | 1122 |
| 1226 | 1122 |
| 1233 | 123 |
| 1234 | 123 |
| 1235 | 123 |
| 1236 | 123 |
| 1244 | 1144 |
| 1245 | 145 |
| 1246 | 246 |
| 1255 | 1155 |
| 1256 | 失去 |
| 1333 | 1133 |
| 1334 | 1133 |
| 1335 | 1133 |
| 1336 | 1133 |
| 1344 | 1144 |
| 1345 | 145 |
| 1346 | 失去 |
| 1355 | 1155 |
| 1356 | 1256 |
| 1444 | 1144 |
| 1445 | 1144 |
| 1446 | 1144 |
| 1455 | 1155 |
| 1456 | 1346 |
| 2222 | 失去 |
| 2223 | 2222 |
| 2224 | 2222 |
| 2225 | 2222 |
| 2226 | 2222 |
| 2233 | 失去 |
| 2234 | 2233 |
| 2235 | 2233 |
| 2236 | 2233 |
| 2244 | 失去 |
| 2245 | 2244 |
| 2246 | 2244 |
| 2255 | 失去 |
| 2256 | 2255 |
| 2333 | 2233 |
| 2334 | 2233 |
| 2335 | 2233 |
| 2336 | 2233 |
| 2344 | 2244 |
| 2345 | 失去 |
| 2346 | 1346 |
| 2355 | 2255 |
| 2356 | 2345 |
| 2444 | 2244 |
| 2445 | 2244 |
| 2446 | 2244 |
| 2455 | 2255 |
| 2456 | 2345 |
| 3333 | 失去 |
| 3334 | 3333 |
| 3335 | 3333 |
| 3335 | 3333 |
| 3336 | 3333 |
| 3344 | 失去 |
| 3345 | 3344 |
| 3346 | 3344 |
| 3355 | 失去 |
| 3356 | 3355 |
| 3444 | 3344 |
| 3445 | 3344 |
| 3446 | 3344 |
| 3455 | 3355 |
| 3456 | 1346 |
Brad S. 写信来信,希望添加一个适用于任意数量珍珠和行数的通用策略。首先,你需要将每一行分解成二进制部分。例如,Transscience 游戏的起始位置如下。
- 3 = 2 + 1
- 4 = 4
- 5 = 4 + 1
- 6 = 4 + 2
然后,你尽量让每个2的幂都留下偶数个。例如,上式中有两个1、两个2和三个4。所以多了一个4。然后,你从任何包含4的行中移除4。继续这样做,直到你能让对手的1的数量减少到2、2或奇数个。
在《珍珠3》游戏中试试这个策略,你每次都能赢。如果你像我在第10局游戏(4+7+8+11)那样一开始就输了,你可以点击“走”让他先走。
别再纠结你的NIM游戏了!我一直以为获胜的关键在于让你的对手(这里指的是计算机)留下的点数加起来等于下一个最小数字,这个数字等于它的二进制总和。也就是说,如果我有17个点,我取2个,剩下15个,也就是二进制数1、2、4、8的总和。但这似乎行不通。我是对还是错?
你在二进制数上的思路没错,但这并非真正的制胜策略。首先,如果你能让对手留下奇数行,每行一个,那就这样做。否则,将每一行分解成二进制元素。例如,99 就是 64+32+2+1。然后把所有行上每个元素的数量加起来。最后,寻找一种能让对手所有行上所有二进制元素数量为偶数的玩法。
我们来看一个例子。假设轮到你了,场景如下。
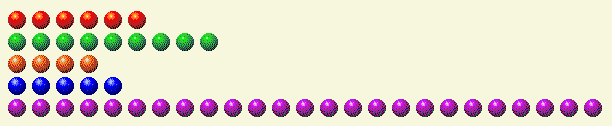
下表将每一行分解为二进制组件。
玩家第 1 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 二十五 | 1 | 0 | 0 | 1 | 1 |
| 全部的 | 3 | 1 | 3 | 2 | 1 |
可以看到,1、2、4 和 16 的数量都是奇数。显然,我们需要让 25 这一行小于 16,才能消除 16 这个数字。为了使二进制数字的和保持偶数,我们需要去掉 1,加上 2,加上 4,保留 8,然后去掉 16。这意味着最佳玩法是最后一行 2+4+8=14。保留最后一行 14,我们得到以下结果。
计算机的第一回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| 全部的 | 2 | 2 | 4 | 2 | 0 |
计算机轮流做事,把这个留给我们。
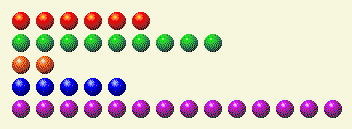
这是它的二进制分解。
玩家第 2 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| 全部的 | 2 | 3 | 3 | 2 | 0 |
这里我们需要去掉一个 2 和一个 4,才能使总数相等。只有一行,也就是 14,包含这两个部分。所以从中去掉 6,剩下 8。
计算机的第二回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| 全部的 | 2 | 2 | 2 | 2 | 0 |
计算机轮流做事,把这个留给我们。
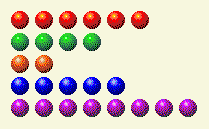
现在我们需要更改 1、4 和 8 列。
玩家第 3 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| 全部的 | 1 | 2 | 3 | 1 | 0 |
可以通过将行 8 更改为 5 来实现,如下所示。
计算机第 3 轮
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 全部的 | 2 | 2 | 4 | 0 | 0 |
计算机轮流做事,把这个留给我们。
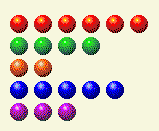
现在我们需要更改 2 和 4 的总数。
玩家回合 4
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 3 | 3 | 0 | 0 |
这可以通过将 6 更改为 0 来实现。
计算机第 4 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 2 | 2 | 0 | 0 |
计算机轮流做事,把这个留给我们。
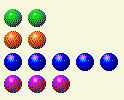
现在我们需要改变 2 和 4。
玩家第 5 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 3 | 1 | 0 | 0 |
这可以通过将 5 行改为 3 行来实现。如果您能让对手陷入 x,x,y,y 局面,您就必然会获胜,前提是您可以将同样的局面保持到最后。
计算机的第 5 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 4 | 0 | 0 | 0 |
接下来的几步,我让计算机继续按照 x,x,y,y 的模式走。这里计算机给我的结果是 2,2,3,2;所以我给它留下的是 2,2,2,2。

然后计算机给了我2,2,1,2。我留下2,2,1,1。
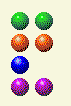
然后计算机给我的结果是2,2,1。我给它留下的是2,2。如果你能把对手的棋子分成两行,你就赢了,只要保持两行棋子相等就行了。

然后计算机给我留下一堆 2,然后我拿走 1。

游戏到此结束。
我最近得到了一个嘉年华轮盘,是我叔祖父的,大概有一百年历史了。我正在尝试用它开发一个游戏。轮盘上的数字从1到60随机排列,每隔十五个标记就会出现一个绿色的星星,黑色和红色交替出现。您能帮我估算一下每次旋转的赔率吗?
因此,有30个黑色号码、30个红色号码和4个绿色号码。这样,黑色中奖的概率为30/64,红色中奖的概率为30/64,绿色中奖的概率为4/64。如果某个事件的概率为p,则公平赔率为(1-p)/p比1。因此,任何红色号码的公平赔率为(34/64)/(30/64) = 34比30 = 17比15。黑色号码的公平赔率为(60/64)/(4/64) = 60比4 = 15比1。对于特定号码,公平赔率为(63/64)/(1/64) = 63比1。
我建议红黑投注赔率为1比1,绿投注赔率为14比1,任何单个数字的赔率为60比1。赌场优势的一个公式是(ta)/(t+1),其中t是真实赔率,a是实际赔率。在本例中,投注红色或黑色的赌场优势为(63-60)/(63+1) = 3/64 = 4.69%。投注绿色的赌场优势为(15-14)/(15+1) = 1/16 = 6.25%。投注单个数字的赌场优势为(63-60)/(63+1) = 3/64 = 4.69%。
在纽约州,场外投注点设有视频彩票终端 (VLT)。当一台视频彩票机“热身”并连续发出一手好牌时,你会听到“机器接近其“设定点””的说法。这就能解释为什么同一台机器有时能赢,有时却不赢。而且,大多数这类机器不允许你输掉一手好牌。如果你输掉一手好牌,它就会给你等值或更好的牌。你对此有什么看法?
VLT 是被美化的拉片游戏。它有一个预先设定的结果池。当你玩的时候,游戏会从结果池中随机选择一个结果,并以老虎机或视频扑克游戏的形式向玩家显示获胜结果。由于结果是注定的,任何技巧因素都是虚构的。例如,如果你拿到了同花大顺,然后把它扔掉,你抽牌时会再得到一张。我通常说,在赌博中过去并不重要,但在这种情况下,存在着“消除效应”。如果你玩了一次输了,那么它会略微提高剩余游戏结果的赔率,直到虚拟拉片的供应耗尽,我猜虚拟转盘会被重新填满。我相信你的忽冷忽热只是正常的运气,任何宿命都是虚构的。
后来,一位读者在该主题中添加了以下内容。
我对你2月14日的“问问巫师”专栏(第183期)有一点看法。其实这和你回答的问题没什么关系,只是你可能会觉得有趣而已。
在1A提案通过(允许全面开展3类博彩)之前,我们曾安装过几年小型的VLT系统。我们的系统由SDG(现为Bally的一部分)运营,奖池初始为400万次抽奖。当奖池缩减至200万时,我们又增加了一个400万的奖池,使总奖池达到600万次抽奖。当奖池再次缩减至200万时,我们又重复了这个过程。
赢得 Yahtzee 需要预计掷多少次?
假设玩家总是持有出现次数最多的数字,则平均值为11.09。下表显示了在8260万次随机模拟试验中,掷骰次数的分布。
骰子实验
| 面包卷 | 发生 | 可能性 |
| 1 | 63908 | 0.00077371 |
| 2 | 977954 | 0.0118396 |
| 3 | 2758635 | 0.0333975 |
| 4 | 4504806 | 0.0545376 |
| 5 | 5776444 | 0.0699327 |
| 6 | 6491538 | 0.0785901 |
| 7 | 6727992 | 0.0814527 |
| 8 | 6601612 | 0.0799227 |
| 9 | 6246388 | 0.0756221 |
| 10 | 5741778 | 0.0695131 |
| 11 | 5174553 | 0.0626459 |
| 12 | 4591986 | 0.0555931 |
| 十三 | 4022755 | 0.0487016 |
| 14 | 3492745 | 0.042285 |
| 15 | 3008766 | 0.0364257 |
| 16 | 2577969 | 0.0312103 |
| 17 | 2193272 | 0.0265529 |
| 18 | 1864107 | 0.0225679 |
| 19 | 1575763 | 0.019077 |
| 20 | 1329971 | 0.0161013 |
| 21 | 1118788 | 0.0135446 |
| 22 | 940519 | 0.0113864 |
| 23 | 791107 | 0.00957757 |
| 24 | 661672 | 0.00801056 |
| 二十五 | 554937 | 0.00671837 |
| 二十六 | 463901 | 0.00561624 |
| 二十七 | 387339 | 0.00468933 |
| 二十八 | 324079 | 0.00392347 |
| 二十九 | 271321 | 0.00328476 |
| 三十 | 225978 | 0.00273581 |
| 31 | 189012 | 0.00228828 |
| 三十二 | 157709 | 0.00190931 |
| 33 | 131845 | 0.00159619 |
| 三十四 | 109592 | 0.00132678 |
| 三十五 | 91327 | 0.00110565 |
| 三十六 | 76216 | 0.00092271 |
| 三十七 | 63433 | 0.00076795 |
| 三十八 | 52786 | 0.00063906 |
| 三十九 | 44122 | 0.00053417 |
| 40 | 36785 | 0.00044534 |
| 41 | 30834 | 0.00037329 |
| 四十二 | 25494 | 0.00030864 |
| 43 | 21170 | 0.0002563 |
| 四十四 | 17767 | 0.0002151 |
| 45 | 14657 | 0.00017745 |
| 46 | 12410 | 0.00015024 |
| 四十七 | 10299 | 0.00012469 |
| 四十八 | 8666 | 0.00010492 |
| 49 | 7355 | 0.00008904 |
| 50 | 5901 | 0.00007144 |
| 51 | 5017 | 0.00006074 |
| 52 | 4227 | 0.00005117 |
| 53 | 3452 | 0.00004179 |
| 54 | 2888 | 0.00003496 |
| 55 | 2470 | 0.0000299 |
| 56 | 2012 | 0.00002436 |
| 57 | 1626 | 0.00001969 |
| 58 | 1391 | 0.00001684 |
| 59 | 1135 | 0.00001374 |
| 60 | 924 | 0.00001119 |
| 61 | 840 | 0.00001017 |
| 62 | 694 | 0.0000084 |
| 63 | 534 | 0.00000646 |
| 64 | 498 | 0.00000603 |
| 65 | 372 | 0.0000045 |
| 66 | 316 | 0.00000383 |
| 67 | 286 | 0.00000346 |
| 68 | 224 | 0.00000271 |
| 69 | 197 | 0.00000238 |
| 70 | 160 | 0.00000194 |
| 71 | 125 | 0.00000151 |
| 72 | 86 | 0.00000104 |
| 73 | 79 | 0.00000096 |
| 74 | 94 | 0.00000114 |
| 75 | 70 | 0.00000085 |
| 76 | 64 | 0.00000077 |
| 77 | 三十八 | 0.00000046 |
| 78 | 四十二 | 0.00000051 |
| 79 | 二十七 | 0.00000033 |
| 80 | 33 | 0.0000004 |
| 81 | 16 | 0.00000019 |
| 82 | 18 | 0.00000022 |
| 83 | 19 | 0.00000023 |
| 84 | 14 | 0.00000017 |
| 85 | 6 | 0.00000007 |
| 86 | 4 | 0.00000005 |
| 87 | 9 | 0.00000011 |
| 88 | 4 | 0.00000005 |
| 89 | 5 | 0.00000006 |
| 90 | 5 | 0.00000006 |
| 91 | 1 | 0.00000001 |
| 92 | 6 | 0.00000007 |
| 93 | 1 | 0.00000001 |
| 94 | 3 | 0.00000004 |
| 95 | 1 | 0.00000001 |
| 96 | 1 | 0.00000001 |
| 97 | 2 | 0.00000002 |
| 102 | 1 | 0.00000001 |
| 全部的 | 82600000 | 1 |
您是否知道任何网站对西洋双陆棋的赔率/统计数据/概率有很好的分析?您是否可以推荐有关该游戏任何方面的特定书籍?
西洋双陆棋是我最喜欢的赌博游戏之一。我没有写过关于它的文章,因为玩家对战游戏极其难分析。而且我似乎也找不到任何可以突破的玩法。所以,我还是把建议留给其他人吧。以下是我推荐的资源:
保罗·马格里尔的《西洋双陆棋》 :如果说西洋双陆棋有一本圣经,那一定是这本了。我骄傲地拥有一本老精装版。这本书会是很好的入门书。虽然这本书写于1976年,但其中的建议仍然适用。
比尔·罗伯蒂的《501道西洋双陆棋基本题》 :多年来我一直想通读这本书,但到现在才完成了一半。一半的题目都答错,真是令人沮丧,甚至让我觉得自己玩西洋双陆棋就像打高尔夫一样糟糕。然而,每错一道题,都蕴藏着宝贵的经验教训。对于中高级棋手来说,这本书是一本宝贵的学习工具,能让人谦卑下来。
Snowie 西洋双陆棋软件:我每年用它下大约1000盘。Snowie 不仅棋艺近乎完美,还能精准地告诉你失误的代价有多大。它还有很多我从未探索过的功能。如果说我从 Snowie 身上学到了什么,那就是我最大的问题在于,有时我看不清明显的走法,从而犯下愚蠢的错误。就像下象棋一样,一步错棋就能毁掉一百步好棋。
Motif 网站:在购买 Snowie 之前,我和 Motif 打过无数盘。在我看来,Motif 的策略非常扎实。没有什么比与更强大的对手比赛更能提升自己的水平了。
在2004年4月11日的专栏中,有一个关于“价格合适”展示摊牌中正确策略的问题。假设遵循最佳策略,那么每个玩家获胜的概率是多少?
下表显示了每位玩家的获胜概率,根据第一位玩家的首次旋转,玩家1先出,然后是玩家2,玩家3最后出。最下面一行显示了首次旋转前的总体获胜概率。
价格合适的展示摊牌中的概率
| 旋转 1 | 战略 | 玩家 1 | 玩家 2 | 玩家 3 |
| 0.05 | 旋转 | 20.59% | 37.55% | 41.85% |
| 0.10 | 旋转 | 20.59% | 37.55% | 41.86% |
| 0.15 | 旋转 | 20.57% | 37.55% | 41.87% |
| 0.20 | 旋转 | 20.55% | 37.55% | 41.9% |
| 0.25 | 旋转 | 20.5% | 37.56% | 41.94% |
| 0.30 | 旋转 | 20.43% | 37.56% | 42.01% |
| 0.35 | 旋转 | 20.33% | 37.58% | 42.10% |
| 0.40 | 旋转 | 20.18% | 37.60% | 42.22% |
| 0.45 | 旋转 | 19.97% | 37.64% | 42.39% |
| 0.50 | 旋转 | 19.68% | 37.71% | 42.61% |
| 0.55 | 旋转 | 19.26% | 37.81% | 42.93% |
| 0.60 | 旋转 | 18.67% | 37.96% | 43.36% |
| 0.65 | 旋转 | 17.86% | 38.21% | 43.93% |
| 0.70 | 停留 | 21.56% | 38.28% | 40.16% |
| 0.75 | 停留 | 28.42% | 35.21% | 36.38% |
| 0.80 | 停留 | 36.82% | 31.26% | 31.92% |
| 0.85 | 停留 | 46.99% | 26.35% | 26.66% |
| 0.90 | 停留 | 59.17% | 20.36% | 20.47% |
| 0.95 | 停留 | 73.61% | 13.19% | 13.21% |
| 1.00 | 停留 | 90.57% | 4.72% | 4.72% |
| 平均的 | 30.82% | 32.96% | 36.22% |
以下是 6×20 6 种可能组合中的获胜数。
玩家 1:118,331,250玩家2:126,566,457
玩家3:139,102,293
按照你的玩法,第三张牌匹配为平局,如果前两张牌之间至少有六个点数差(六张牌差),赔率就会对你有利。我在奥兰治县玩的时候,第三张牌匹配的结果是双输。根据这条规则,八张牌差的赔率是收支平衡的。如果第三张牌匹配的结果是一倍输,那么你需要七张牌差的赔率才能对你有利。
单张扑克游戏有三张牌,一张 A、一张 2 和一张 3。A 最小,3 最大。两位玩家各向底池下注 1 美元。然后,每位玩家拿到一张牌。下注顺序是预先确定的,玩家 1 先行动。玩家 1 可以下注 1 美元或过牌。如果玩家 1 下注,玩家 2 可以跟注或弃牌。如果玩家 1 过牌,那么玩家 2 可以下注 1 美元或过牌。如果玩家 1 过牌,玩家 2 下注,那么玩家 1 可以跟注或弃牌。如果两位玩家都过牌或都下注,那么牌值较大的玩家赢得底池。假设两位玩家都是完美的逻辑学家,那么每位玩家的最佳策略是什么?
希望你满意;我花了一整天时间研究这个问题。答案和解答可以在我的另一个网站mathproblems.info上的第 203 题找到,或者在 Jason Swanson 的学术论文《博弈论与扑克》中找到。
我正在四处寻找抵押贷款。一家公司提供的30年期固定利率贷款利率为5.75%,另加一个点。另一家公司提供的利率为5.875%,不加点。哪家公司更划算?
为了方便其他读者理解,点数指的是贷款收取的佣金。例如,一笔25万美元的贷款,一个点数就是2500美元。我假设借款人会把这个点数加到本金余额中,并且绝不会提前偿还本金。
下表为按一个点的利率和期限计算的无点等值利率。
无点数的等值利率
| 一点利率 | 10年 | 15年 | 20年 | 30年 | 40年 |
| 4.00% | 4.212% | 4.147% | 4.115% | 4.083% | 4.067% |
| 4.25% | 4.463% | 4.398% | 4.366% | 4.334% | 4.318% |
| 4.50% | 4.714% | 4.649% | 4.617% | 4.585% | 4.570% |
| 4.75% | 4.965% | 4.900% | 4.868% | 4.836% | 4.821% |
| 5.00% | 5.216% | 5.151% | 5.119% | 5.088% | 5.073% |
| 5.25% | 5.467% | 5.402% | 5.370% | 5.339% | 5.324% |
| 5.50% | 5.718% | 5.654% | 5.621% | 5.590% | 5.576% |
| 5.75% | 5.969% | 5.905% | 5.873% | 5.842% | 5.827% |
| 6.00% | 6.220% | 6.156% | 6.124% | 6.093% | 6.079% |
| 6.25% | 6.471% | 6.407% | 6.375% | 6.344% | 6.330% |
| 6.50% | 6.723% | 6.658% | 6.626% | 6.596% | 6.582% |
| 6.75% | 6.974% | 6.909% | 6.878% | 6.847% | 6.834% |
| 7.00% | 7.225% | 7.160% | 7.129% | 7.099% | 7.085% |
| 7.25% | 7.476% | 7.412% | 7.380% | 7.350% | 7.337% |
| 7.50% | 7.727% | 7.663% | 7.631% | 7.602% | 7.589% |
| 7.75% | 7.978% | 7.914% | 7.883% | 7.853% | 7.841% |
| 8.00% | 8.229% | 8.165% | 8.134% | 8.105% | 8.093% |
| 8.25% | 8.480% | 8.416% | 8.385% | 8.357% | 8.344% |
| 8.50% | 8.731% | 8.668% | 8.637% | 8.608% | 8.596% |
| 8.75% | 8.982% | 8.919% | 8.888% | 8.860% | 8.848% |
| 9.00% | 9.233% | 9.170% | 9.140% | 9.112% | 9.100% |
| 9.25% | 9.485% | 9.421% | 9.391% | 9.363% | 9.352% |
| 9.50% | 9.736% | 9.673% | 9.642% | 9.615% | 9.604% |
| 9.75% | 9.987% | 9.924% | 9.894% | 9.867% | 9.856% |
| 10.00% | 10.238% | 10.175% | 10.145% | 10.119% | 10.108% |
这表明,5.75% 的利率加上一个点,相当于 5.842% 的利率(没有点)。换句话说,假设收取的点数加到本金余额中,两种情况的还款金额相同。您的另一个报价是 5.875% 的利率(没有点数),高于 5.842%,所以我会选择 5.75% 的利率(加上点数)。
PS 对于那些想知道我如何求解 i 的人,我使用了 Excel 中的速率函数。
我儿子两周内刚刚打出两个一杆进洞。这几率是多少?我儿子的差点是1。第一个洞151码,第二个洞137码,在两个不同的球场。
根据格雷戈里·贝尔 (Gregory Baer) 所著的《人生:概率(以及如何提高概率)》 ,在 PGA 巡回赛中,在标准杆 3 杆洞中一杆进洞的概率是 2491 分之一。我相信这些距离都属于标准杆 3 杆范围内。
1差点已经很不错了,所以跟美巡赛球员相比,我不会打太大折扣。假设你儿子每杆3杆洞的概率是3000分之一。一个典型的高尔夫球场大约有四个3杆洞。假设你儿子每天都打球,那么他一周要打28个3杆洞。那么恰好打出两个一杆进洞的概率就是 (28,2)×(1/3000) ² ×(2999/3000) ²² =24017分之一。
我最近参加了一个抽奖活动,奖品有7033个,据说中奖概率是1/13。我买了5张彩票。我实际中奖概率是多少?另外,大奖有40个。我中大奖的概率是多少?
为了简单起见,我们忽略这样一个事实:你买的彩票越多,每张彩票的价值就越低,因为你是在与自己竞争。也就是说,输掉五张彩票的概率是 (12/13) 5 = 67.02%。所以至少赢得一次奖的概率是 32.98%。在你买彩票之前,彩票桶里总共有 7033×13=91,429 张彩票。91,429-40=91,389 张彩票不是大奖。五张彩票中不了大奖的概率是 (91,389/91429) 5 = 99.78%。所以至少赢得一次大奖的概率是 0.22%,也就是 458 分之一。
在红桃游戏中,每位玩家有13张牌。其中牌数最多的花色称为“长花”,其花色可以是4到13张。这些花色总数的概率是多少?
红桃长花的概率
| 牌 | 组合 | 可能性 |
| 4 | 222766089260 | 0.35080524800183 |
| 5 | 281562853572 | 0.44339660045899 |
| 6 | 105080049360 | 0.16547685914958 |
| 7 | 22394644272 | 0.03526640326564 |
| 8 | 2963997036 | 0.00466761219692 |
| 9 | 235237860 | 0.00037044541245 |
| 10 | 10455016 | 0.00001646424055 |
| 11 | 231192 | 0.00000036407412 |
| 12 | 2028 | 0.00000000319363 |
| 十三 | 4 | 0.00000000000630 |
| 全部的 | 635013559600 | 1 |
72法则指的是,用年回报率除以72,就能算出你的资金翻倍所需的年数。例如,一项年回报率为10%的投资,需要72/10=7.2年才能翻倍。我有个有点无聊的问题:为什么是72年?
首先,“72法则”只是对资金翻倍所需时间的近似估计,而非确切答案。下表列出了不同年利率下“72法则”的数值以及确切的年数。
72法则——金钱翻倍的年限
| 利率 | 72法则 | 精确的 | 不同之处 |
|---|---|---|---|
| 0.01 | 72.00 | 69.66 | 2.34 |
| 0.02 | 36.00 | 35.00 | 1.00 |
| 0.03 | 24.00 | 23.45 | 0.55 |
| 0.04 | 18.00 | 17.67 | 0.33 |
| 0.05 | 14.40 | 14.21 | 0.19 |
| 0.06 | 12.00 | 11.90 | 0.10 |
| 0.07 | 10.29 | 10.24 | 0.04 |
| 0.08 | 9.00 | 9.01 | -0.01 |
| 0.09 | 8.00 | 8.04 | -0.04 |
| 0.10 | 7.20 | 7.27 | -0.07 |
| 0.11 | 6.55 | 6.64 | -0.10 |
| 0.12 | 6.00 | 6.12 | -0.12 |
| 0.13 | 5.54 | 5.67 | -0.13 |
| 0.14 | 5.14 | 5.29 | -0.15 |
| 0.15 | 4.80 | 4.96 | -0.16 |
| 0.16 | 4.50 | 4.67 | -0.17 |
| 0.17 | 4.24 | 4.41 | -0.18 |
| 0.18 | 4.00 | 4.19 | -0.19 |
| 0.19 | 3.79 | 3.98 | -0.20 |
| 0.20 | 3.60 | 3.80 | -0.20 |
为什么是 72?不一定非要恰好是 72。这只是一个与实际投资利率相符的数字。它几乎恰好对应于 7.8469% 的利率。72 本身并没有什么特别之处,就像 π 或 e 一样。为什么任何数字都可以呢?假设利率是 i,那么我们来计算一下投资翻倍所需的年数 (y)。
2 = (1+i) y
ln(2)= ln(1+i) y
ln(2)= y×ln(1+i)
y = ln(2)/ln(1+i)
这可能不是我迄今为止最好的答案,但请尝试遵循这个逻辑:让 y=ln(x)。
dy/dx=1/x。
当 x 的值接近于 1 时,1/x =~ x。
因此,当 x 值接近于 1 时,dy/dx =~ 1。
因此,当 x 值接近 1 时,ln(x) 的斜率将接近 1。
因此,当 x 值接近于 0 时,ln(1+x) 的斜率将接近于 1。
“72 规则”是指 .72/i =~ .6931/ln(1+i)。
我们已经确定,当 i 的值接近于 0 时,i 和 ln(1+i) 相似。
因此,当 i 的值接近于 0 时,1/i 和 1/ln(1+i) 相似。
使用 72 而不是 69.31 可以调整 i 和 ln(1+i) 之间的差异,使 i 的值在 8% 左右。
希望你理解得通。我的微积分学得有点生疏,我花了好几个小时才解释清楚。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
最近在一次街头集市上,他们玩了一个游戏,里面有一块数字区域,里面有一些浅杯子和一个装满球的杯子,游戏涉及加法。我没有问这个游戏的名字,在网上搜索了大约一个小时,但什么也没找到。我以为你可能有一些关于它的信息,比如它的概率,或者至少知道它的名字。
这款游戏的行业术语是Razzle Dazzle。我记得小时候在南加州见过,去年在墨西哥圣费利佩也见过。它通常被设计成看起来像一场足球比赛。在我看来,这款游戏是嘉年华游戏骗局中最恶劣的。纽约州应该为允许这种游戏而感到羞耻。根据一些研究,虽然各个地方的规则各不相同,但骗局的本质总是一样的。
它基于与掷骰子游戏中的“场地投注”相同的原理。对于那些不熟悉“场地投注”的读者来说,如果两颗骰子掷出的总点数为2、3、4、9、10、11或12,玩家就赢了。输的点数为5、6、7和8。赢的赔率相同,但掷出2的赔率为2比1,掷出12的赔率为3比1(在吝啬的哈拉斯赌场除外,那里只有掷出12的赔率为2比1)。数学能力较弱的赌徒可能会错误地认为这是一个不错的赌注,因为有7个点数会赢,只有4个点数会输。赔率对赌场有利的原因是,掷出输的点数的可能性最大。
以下是 Razzle Dazzle 的具体规则,摘自唐纳德·A·贝里 (Donald A. Berry) 和罗纳德·R·瑞格尔 (Ronald R. Regal) 撰写的《赢得某场嘉年华游戏的概率》一文,该文发表在 1978 年 11 月的《美国统计学家》杂志上。
- 游戏的目标是在足球场上前进100码。玩家完成目标后将获得一些奖励。
- 玩家每次玩时开始支付指定的费用,例如 1 美元。
- 玩家将把 8 颗弹珠投掷到 11 x 13 的网格上。每颗弹珠都会落入 143 个孔中的一个。
- 每个洞都有从 1 到 6 的点数。下表显示了每个点数的频率。
Razzle Dazzle 积分分配
积分 数字
在船上可能性 1 11 0.076923 2 19 0.132867 3 三十九 0.272727 4 四十四 0.307692 5 19 0.132867 6 11 0.076923 全部的 143 1.000000 - 总分将被累加。裁判员将在换算表上查找总分,以计算出选手前进了多少码。换算表如下所示。
Razzle Dazzle转换表
积分 码
获得8 100 9 100 10 50 11 三十 12 50 十三 50 14 20 15 15 16 10 17 5 18至38岁 0 三十九 5 40 5 41 15 四十二 20 43 50 四十四 50 45 三十 46 50 四十七 100 四十八 100 - 如果玩家掷出的总点数为 29,则所有后续掷骰的费用将翻倍,并且当玩家到达足球场的另一端时,他将获得一个额外的奖品。
每颗弹珠的平均得分为 3.52 分,标准差为 1.31。请注意,3 分和 4 分的概率最高。这使得标准差保持在较低水平,并且多颗弹珠的总得分接近预期。相比之下,单个骰子掷出的标准差为 1.71。
接下来,请注意码数转换表上总共有20个获胜结果和21个失败结果。那些在嘉年华游戏上赌博的傻瓜可能会错误地认为他们的晋级概率是20/41或48.8%。如果嘉年华工作人员谎称这是晋级概率,我一点也不会感到惊讶。然而,就像场地投注一样,最有可能的结果并不会赢任何东西。
下表显示了每回合得分、码数和预期码数的概率。右下角单元格显示每回合平均码数为0.0196。
每回合预计获得码数
| 积分 | 可能性 | 码 获得 | 预期的 码 获得 |
| 8 | 0.00000000005 | 100 | 0.00000000464 |
| 9 | 0.00000000176 | 100 | 0.00000017647 |
| 10 | 0.00000002586 | 50 | 0.00000129285 |
| 11 | 0.00000022643 | 三十 | 0.00000679305 |
| 12 | 0.00000143397 | 50 | 0.00007169849 |
| 十三 | 0.00000713000 | 50 | 0.00035650022 |
| 14 | 0.00002926510 | 20 | 0.00058530196 |
| 15 | 0.00010234709 | 15 | 0.00153520642 |
| 16 | 0.00031168305 | 10 | 0.00311683054 |
| 17 | 0.00083981462 | 5 | 0.00419907311 |
| 18 | 0.00202563214 | 0 | 0.00000000000 |
| 19 | 0.00441368617 | 0 | 0.00000000000 |
| 20 | 0.00874847408 | 0 | 0.00000000000 |
| 21 | 0.01586193216 | 0 | 0.00000000000 |
| 22 | 0.02642117465 | 0 | 0.00000000000 |
| 23 | 0.04056887936 | 0 | 0.00000000000 |
| 24 | 0.05757346716 | 0 | 0.00000000000 |
| 二十五 | 0.07566411880 | 0 | 0.00000000000 |
| 二十六 | 0.09221675088 | 0 | 0.00000000000 |
| 二十七 | 0.10431970222 | 0 | 0.00000000000 |
| 二十八 | 0.10958441738 | 0 | 0.00000000000 |
| 二十九 | 0.10689316272 | 0 | 0.00000000000 |
| 三十 | 0.09677806051 | 0 | 0.00000000000 |
| 31 | 0.08125426057 | 0 | 0.00000000000 |
| 三十二 | 0.06317871335 | 0 | 0.00000000000 |
| 33 | 0.04540984887 | 0 | 0.00000000000 |
| 三十四 | 0.03009743061 | 0 | 0.00000000000 |
| 三十五 | 0.01833921711 | 0 | 0.00000000000 |
| 三十六 | 0.01023355162 | 0 | 0.00000000000 |
| 三十七 | 0.00520465303 | 0 | 0.00000000000 |
| 三十八 | 0.00239815734 | 0 | 0.00000000000 |
| 三十九 | 0.00099365741 | 5 | 0.00496828705 |
| 40 | 0.00036673565 | 5 | 0.00183367827 |
| 41 | 0.00011909673 | 15 | 0.00178645089 |
| 四十二 | 0.00003349036 | 20 | 0.00066980729 |
| 43 | 0.00000797528 | 50 | 0.00039876403 |
| 四十四 | 0.00000155945 | 50 | 0.00007797235 |
| 45 | 0.00000023832 | 三十 | 0.00000714969 |
| 46 | 0.00000002632 | 50 | 0.00000131607 |
| 四十七 | 0.00000000176 | 100 | 0.00000017647 |
| 四十八 | 0.00000000005 | 100 | 0.00000000464 |
| 总计 | 1.00000000000 | 0 | 0.01961648451 |
以下是对 1750 万场游戏进行随机模拟的一些结果。
Razzle Dazzle 模拟结果
| 问题 | 回答 |
| 每回合晋级的概率 | 0.0028 |
| 预计每回合获得码数 | 0.0196 |
| 每次推进预计获得码数 | 6.9698 |
| 每场比赛预期回合数 | 5238.7950 |
| 每场比赛平均双打数 | 559.9874 |
| 每场比赛平均奖金 | 560.9874 |
我本来想指出每场游戏的平均总投注额,但我的电脑无法处理这么大的数字。在平均每场5239轮的游戏中,玩家平均加倍投注560次。模拟中的一局游戏,玩家加倍投注1800次。即使平均加倍560次,假设起始投注额为1美元,每轮的投注额也高达3.77×10^ 168美元。这比已知宇宙中的原子数量还要大几个数量级(来源)。
即使是最幼稚的玩家,如果每355次才晋级一次,也玩不了多久。嘉年华工作人员一开始会做的就是为了玩家好而作弊。他们可能会发现玩家有免费掷骰子的机会,或者在加分时撒谎,让玩家赢取总分,以增强他们的信心。我从未玩过这个游戏,但我猜想,当玩家接近红区(距离触地得分20码或更短)时,嘉年华工作人员就会开始公平地比赛。玩家可能会想知道为什么自己突然一无所获,但既然已经投入了资金,而且距离终点线如此之近,他肯定不会轻易放弃,放弃已经支付的码数。
链接
- 《Razzle Dazzle》 ,摘自《On the Midway》一书。
- Razzle Dazzle Carny 棋盘游戏街机骗局。
- 唐纳德·A·贝里和罗纳德·R·里格尔合著的《赢得某场嘉年华游戏的概率》
最近的一个嘉年华推出了一款井字棋游戏。游戏价格为1英镑,玩家需要将三个弹力十足的球扔向一个底部有9个格子的大木箱。假设每个球都落在不同的格子里,那么获胜的概率是多少?
有八种获胜方式:三行、三列和两条对角线。从 9 个方格中抽出 3 个,一共有(9,3)=84 种组合方式。因此,获胜概率为 8/84 = 9.52%。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
您对玩大富翁游戏有什么建议?
这是我的巫师玩大富翁游戏的基本策略:
- 买下所有东西。如果房产无法帮助你垄断、阻止他人,或者作为筹码的价值不高,高级玩家可能会破例。在资金短缺的情况下,公共设施也可能被拒绝。
- 尽可能地交易。这就是技巧的用武之地。尽量交易你能交易到的最佳套装。我通常将它们按以下顺序排列:橙色、黄色、浅蓝色、深蓝色、浅紫色、红色、绿色、深紫色。具体顺序会根据具体情况而有所不同。在资金紧张的游戏中,优先选择开发成本较低的套装,例如浅蓝色套装。在资金充裕的游戏中,选择那些更有可能花钱购买的套装,例如黄色或深蓝色套装。
- 一旦你拥有一套房产,无论是自然而然的还是通过交易获得的,都要迅速积累。尽量尽快在每处房产上建三栋房子。三栋之后,每栋房子的边际收益率就会下降。把大部分其他房产抵押出去,把现金花掉。你应该留下一点净资产来应对一些小开支。不花钱就像战场上的士兵不用子弹一样。
- 反对所有愚蠢的规则。尤其要反对“免费停车”的奖金池(我受不了那个!)。如果你比对手更熟练,你就应该尽量减少游戏的随机性。
如果一只猴子在玩魔方,那么在任意给定时间,它处于解出的图案中的概率是多少?
魔方的六个中心面是固定的。旋转这些面只能重新排列角和棱。如果将魔方拆开,那么无论每个部分的方向如何,八个角的排列方式就有 8!=40,320 种。同样,无论方向如何,十二条棱的排列方式也有 12!=479,001,600 种。
每个角有 3 种方向,总共有 3 8 = 6,561 种角方向。同样,每个边块有两种方向,总共有 2 12 = 4,096 种边方向。
所以,如果我们把魔方拆开,重新排列棱角,那么就会有 8! × 12! × 3 8 × 2 12 = 519,024,039,293,878,000,000 种可能的排列组合。然而,并非所有这些排列组合都能通过旋转面从起始位置得到。
首先,不可能只旋转一个角,而其他部分保持不变。任何旋转组合都无法做到这一点。基本上,每个动作都必须有一个反应。如果你想旋转一个角,它会以某种方式干扰其他棋子。同样,也不可能只翻转一个边棋子。出于这些原因,我们必须将排列数除以 3 × 2 = 6。
其次,在不干扰魔方其他部分的情况下,不可能交换两个边块。这是这个答案中最难解释的部分。魔方所能做的就是每次旋转一个面。每次转动都会旋转四个边块和四个角块,总共移动八个块。一系列旋转可以用能被 8 整除的块移动次数来表示。通常,一系列移动会导致两个移动相互抵消。但是,任何旋转序列都会移动偶数个块。交换两个边块需要一个移动次数,即奇数次,这不能通过任何偶数集的总和来实现。数学家称之为奇偶校验问题。因此我们必须再除以 2,因为在不干扰其他块的情况下无法交换两个边块。
因此,魔方的排列组合共有 3 × 2 × 2 = 12 种可能。如果你拆开一个魔方,然后随机地重新组装,那么有 1/12 的概率,它能够被解开。因此,魔方的排列组合总数为 8! × 12! × 3 (12) × 2 (12/12 ) = 43,252,003,274,489,900,000。如果有 70 亿只猴子(大约相当于世界人口)随机玩魔方,以每秒旋转一次的速度,魔方平均每 196 年就会经过一次解开的位置。
链接
我玩的是红心大战,拿到了10张。这概率是多少?
对于不熟悉红心牌规则的人来说,游戏开始时会给四位玩家各发13张牌。红心花色对游戏至关重要,所以你拿到多少张红心也很重要。下表显示了拿到0到13张红心的概率。
13 张牌中出现 0 至 13 颗红心的概率
| 红心 | 组合 | 可能性 | 逆 |
|---|---|---|---|
| 十三 | 1 | 0.0000000000016 | 1比635,013,559,600.0 |
| 12 | 507 | 0.0000000007984 | 1比1,252,492,228.0 |
| 11 | 57,798 | 0.0000000910185 | 10,986,773.9分之一 |
| 10 | 2,613,754 | 0.0000041160601 | 242,950.8分之1 |
| 9 | 58,809,465 | 0.0000926113531 | 10,797.8 分之一 |
| 8 | 740,999,259 | 0.0011669030492 | 1比857.0 |
| 7 | 5,598,661,068 | 0.0088166008164 | 1比113.4 |
| 6 | 26,393,687,892 | 0.0415639752774 | 1比24.1 |
| 5 | 79,181,063,676 | 0.1246919258321 | 1比8.0 |
| 4 | 151,519,319,380 | 0.2386080062219 | 1比4.2 |
| 3 | 181,823,183,256 | 0.2863296074662 | 1比3.5 |
| 2 | 130,732,371,432 | 0.2058733541286 | 1比4.9 |
| 1 | 50,840,366,668 | 0.0800618599389 | 1/12.5 |
| 0 | 8,122,425,444 | 0.0127909480376 | 78.2分之1 |
| 全部的 | 635,013,559,600 | 1.0000000000000 |
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
对于那些仍然使用普通彩票(而非电子彩票)的赌场促销活动,玩家需要在玩家柜台打印彩票,然后将其放入转鼓中——在将彩票放入转鼓之前,你们会弯曲/折叠彩票吗?你认为弯曲的彩票被抽中的几率更大吗?
希望你满意。为了回答这个问题,我在Office Depot买了一大卷彩票。然后我把其中500张彩票放进一个纸袋里,一半对折,大约90度角,另一半展开。之后,我让六位志愿者每人每次抽取40到60张彩票,并进行替换,同时我记录结果。结果如下。
抽奖券实验
| 主题 | 折叠 | 展开 | 全部的 |
|---|---|---|---|
| 1 | 二十五 | 二十五 | 50 |
| 2 | 三十八 | 22 | 60 |
| 3 | 二十五 | 15 | 40 |
| 4 | 三十四 | 16 | 50 |
| 5 | 二十七 | 23 | 50 |
| 6 | 二十六 | 24 | 50 |
| 全部的 | 175 | 125 | 300 |
因此,抽出的彩票中有 58.3% 被折叠了!
如果假设弃牌没有影响,那么这些结果将与预期相差2.89个标准差。假设弃牌不影响中奖概率,那么获得这么多或更多弃牌彩票的概率为0.19%,即514分之一。
我想补充的是,那些匆忙抽奖的受试者更有可能抽到弃牌。而那些每次抽奖都小心谨慎的受试者,抽到弃牌的概率接近或接近一半一半。
所以,我的结论肯定是放弃它们。
有关此问题的讨论,请访问我在Wizard of Vegas 的论坛。