花旗骰 - 骰子和滚动
我想知道如何改变掷骰子游戏中的骰子,以便每次掷出 7 或 11,您能帮忙吗?谢谢。
然后进行修改,使一个骰子的每一面都是六,而另一个骰子的每一面都是一和五。
你认为玩家的“一厢情愿”会影响游戏结果吗?请注意,我关心的不是影响的大小,而是你的哲学观点。另外,你认为玩家在玩掷骰子游戏时掷骰子的方式会导致结果偏差(好或坏)吗?你的网站一如既往地棒极了。
谢谢你的赞美。不,我认为在其他条件相同的情况下,这种一厢情愿的想法在赌场里没什么用。
关于骰子影响力的问题一直备受争议。我个人对此持怀疑态度。当我在2013年回顾这篇回复时,我仍然没有看到令人信服的证据,表明有人能够施加足够的影响力来获得优势。
只是想知道您对通过预先设置骰子来改变掷骰子中的频率表的看法。
我对此非常怀疑。我在我的掷骰子附录3中回顾了一些关于这个主题的实验。
我最近学到了一些关于掷骰子游戏的骰子设置策略。有些人认为,你可以在投掷前以某种方式设置骰子,通过让骰子只围绕一个旋转轴旋转,在某些骰子组合下,掷出“7”的概率就会降低。我想知道这种说法是否属实,还是只是一种谬论。
我不相信。到目前为止,我还没看到任何我尊敬的人支持这种方法,也没有任何证据表明它有效。虽然我不完全排除这种可能性,但我对此非常怀疑。我虽然住在内华达州,但说到像骰子设置这样的事情,我来自密苏里州,“给我看看”它是否有效。
骰子真的没有偏见吗?数字较大且孔洞较多的面似乎比数字较小且孔洞较少的面更轻。这似乎表明,较重的面更有可能面朝下落地,而数字较大的面更有可能面朝上落地。我可以想象一个可以尝试利用这一原理的掷骰子游戏系统,但我不知道它是否真的有效。你觉得呢?
对于普通骰子,比如你在棋盘游戏中得到的骰子,确实如此。然而,赌场骰子上镶嵌着点。他们在工厂里为这些点钻孔,然后将白色点嵌入孔中,这些点的密度与骰子本身相同。所以骰子本质上是一个完美的立方体。即使他们使用普通的棋盘游戏骰子,我也怀疑这种偏差是否足以克服赌场优势。
您是否相信赌场掷骰子游戏中掷骰子的过程与 RNG 一样是真正随机的,或者是否存在掷骰子“机制”或纯粹的草率投掷(例如短距离投掷)导致掷骰子好与掷骰子差的情况,如果现实世界中的赌场掷骰子游戏不是真正随机的,我该如何利用这一点?
我认为不存在天生掷骰子能力差的人。除了少数专业玩家外,所有掷骰子都可以被认为是真正随机的。有一些研讨会教你如何通过进动掷骰子来克服赌场优势,但我既不赞成也不反对这种做法。我还没有看到足够的证据来证明这一点。
在《赌场玩家》杂志十月刊上,弗兰克·斯科布莱特写了一篇关于控制掷骰子的文章,文中你提到斯坦福·黄在500次掷骰子中只掷出74个7,你输了1800美元。你为什么要押注这么小的样本(500次)?一个声称能够控制骰子的人应该愿意至少掷5万次来证明自己的技术。我认为500次掷骰子样本太小,几乎任何事情都可能发生,这难道错了吗?
我把1800美元输给了另一位赌博作家,而不是斯坦福。我本来希望掷出更多骰子,但显然时间有限。假设每分钟掷一次,掷50000次骰子需要34.7天。500次不是我决定的,但这似乎是在大样本量和时间之间做出的合理妥协。你说得对,500次太少了,不足以充分说明影响骰子行为的合理性,但500次总比零次好。
我知道你对骰子控制持怀疑态度。我已经练习了三个月的掷骰子和控制投掷了。随机掷了655次,掷出78个7的概率是多少?谢谢你的帮助 :)
对于大量投掷,我们可以使用高斯曲线近似。655次投掷中,预期出现7的次数为655 × (1/6) = 109.1667。方差为655 × (1/6) × (5/6) = 90.9722。标准差为sqr(90.9722) = 9.5379。您的78次投掷结果比预期值低109.1667 − 78 = 31.1667。这相当于(31.1667 - 0.5)/9.5379 = 3.22个标准差。低于预期3.22个或更多标准差的概率为0.000641,即1/1560。我在Excel中使用公式normsdist(-3.22)得出了这个数字。
这是关于掷骰子游戏的骰子控制。您之前讨论过斯坦福·黄实验,其中提到:“赌注的条件是,精准投掷者在500次掷骰子中能否掷出少于79.5个7。在随机游戏中,预期数字是83.33。在500次随机掷骰子中掷出79个或更少7的概率是32.66%……在500次随机掷骰子中掷出74个或更少7的概率是14.41%。”
我对这个赌注的疑问是,14.41% 仍然不是“统计上显著的” [即 p < 0.05],这通常被认为意味着距离平均值大于两个标准差 - 或者事件在系列的任一端随机发生的概率小于*综合* 5%。
在您可以说结果完全随机(即结果具有统计意义)的可能性小于 2.5% 之前,需要在 500 次投掷中投出多少个“7”?
非常感谢,顺便说一句,您的网站绝对是我发现的有关赌博赔率和概率的最佳网站......继续努力!!!
谢谢你的赞美。你不应该说投掷结果非随机的概率是p。应该这样表述:一场随机游戏产生这种结果的概率是p。没人指望500次投掷就能证明或反驳任何事情。我并没有把79.5个7的点数定为79.5,但我怀疑这个点数是否具有统计学意义;相反,我怀疑这是一个双方都会同意下注的点。
2.5% 的显著性水平是与预期值相差 1.96 个标准差。这可以在 Excel 中使用公式 =normsinv(0.025) 计算得出。500 次投掷的标准差为 sqr(500*(1/6)*(5/6)) = 8.333。因此,1.96 个标准差等于 1.96 * 8.333 = 16.333 次,比预期值低。500 次投掷中出现七的预期次数为 500*(1/6) = 83.333。因此,比预期值低 1.96 个标准差等于 83.333 − 16.333 = 67。使用二项分布检验,出现 67 次或更少七的准确概率为 2.627%。
三年前,您在“问问巫师”专栏中写道:“您说得对,500次掷骰子太少,不足以充分论证影响骰子结果的合理性,但500次掷骰子总比零次好。” 您能否描述一下,在实验中,您需要对所谓的骰子影响者进行哪些操作,才能让您有足够的信心开始对他进行大额投注?我之所以问这个问题,是因为在某些二十一点模拟游戏中,10亿轮掷骰子是“可靠”结果的良好基准。在最高效(即需要最少掷骰次数)的实验设计下,投掷者需要掷多少次才能确信自己能够影响结果?我知道答案取决于投掷者的技能,但您明白我的意思。即使在最好的情况下,如果也需要掷一百万次,那么这项尝试就不值得了。
信心的建立没有明确的标准,关键在于程度。首先,我会问测试的目的是什么,以及射手对结果的估计。任何测试都可能出现两种错误。一个熟练的射手可能会因为运气不好而失败,或者一个随机的射手可能会因为运气好而通过。在这两种情况下,我更倾向于避免假阳性。我认为合理的测试应该将假阴性的概率设定在5%左右,将假阳性的概率设定在1%左右。
例如,假设索赔人声称他平均每掷七次骰子就能掷出一个七。而随机掷骰子的人平均每掷六次就能掷出一个七。通过反复试验,我发现,要同时满足这两个条件,测试需要掷骰子3600次,并且需要547个或更少的七才能通过,或者每6.58次掷出一个七。
一位七分之一的射手平均应该能打出514.3个七分,标准差为21.00。使用高斯近似,这位技术娴熟的射手投出548个或更多七分(假阴性)的概率为5.7%。一位随机射手平均应该能打出600个七分,标准差为22.36。一位随机射手通过测试(假阳性)的概率为0.94%。下图显示了技术娴熟和随机射手的可能结果。如果结果在绿线左侧,那么我认为该射手通过了测试,我会押注他获胜。
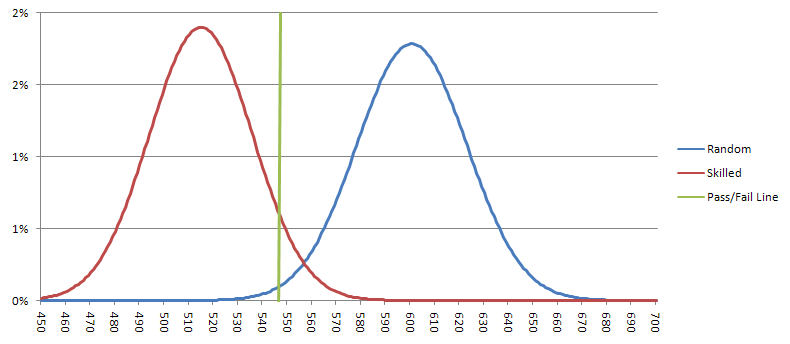
实际的难题是,如果我们假设每分钟投掷两次,那么进行测试将需要30个小时。或许我可以更自由地设定显著性水平,以减少时间要求,但结果可能不那么令人信服。我确实认为,现在是时候进行比500次投掷的黄氏实验更大规模的测试了。
今天的新闻是,大西洋城的一名女子在Borgata 赌场连续掷骰子 154 次才掷出 7 点。这意味着她掷了 154 次骰子,没有一次掷出 7 点。所以我取 (30/36) 154 ,得出的概率超过 1.5 万亿分之一。赢得超级百万彩票的概率比连续掷 154 次非 7 点骰子马拉松的概率高出约 9,000 倍。考虑到这种情况发生的可能性微乎其微,而且人们被定罪的 DNA 证据中存在虚假匹配的概率仅为数十亿分之一,您会怀疑这是作弊行为吗?您会就此事咨询 Borgata 赌场吗?我已经打电话给他们,告诉他们我的名字,并告诉他们想怎么处理就怎么处理。我很想知道您的想法。
首先,她总共掷了 154 次骰子,第 154 次掷出了 7( 来源:NJ.com )。但是,这并不意味着她在前 153 次掷骰子中从未掷出过 7。她可以在 come out 掷骰子时掷出很多 7。正如我在2003 年 5 月 3 日的专栏中指出的那样,掷到第 154 次的概率是 56 亿分之一。赢得超级百万大奖的概率是 1 / (56,5)*46 = 175,711,536。因此,掷 154 次或更多次的难度大约是 32 倍。如果有足够的时间和表格(我认为是存在的),这样的事情迟早会发生。所以,我不会怀疑有人作弊。我粗略估计这种情况在任何一年发生的概率约为 1%。
另请参阅我在mathproblems.info上以矩阵表示的解决方案,问题 204。
我认为拉斯维加斯的一些赌场使用的骰子是单面加重的。为了证明这一点,我提交了在拉斯维加斯大道一家赌场收集的244次投掷结果。公平的骰子能产生如此偏差的结果,几率有多大?
| 骰子测试数据 | |
| 骰子总数 | 观察 |
| 2 | 6 |
| 3 | 12 |
| 4 | 14 |
| 5 | 18 |
| 6 | 23 |
| 7 | 50 |
| 8 | 三十六 |
| 9 | 三十七 |
| 10 | 二十七 |
| 11 | 14 |
| 12 | 7 |
| 全部的 | 244 |
7.7%。
卡方检验非常适合这类问题。要使用该检验,对每个类别取 (ae) 2 /e,其中 a 是实际结果,e 是预期结果。例如,投掷 244 次,总点数为 2 的预期次数为 244×(1/36) = 6.777778。如果您不明白为什么投掷 2 的概率是 1/36,请阅读我的骰子概率基础知识页面。对于总点数为 2 的卡方值,a=6,e=6.777778,因此 (ae) 2 /e = (6-6.777778) 2 /6.777778 = 0.089253802。
卡方结果
| 骰子总数 | 观察 | 预期的 | 卡方检验 |
| 2 | 6 | 6.777778 | 0.089253 |
| 3 | 12 | 13.555556 | 0.178506 |
| 4 | 14 | 20.333333 | 1.972678 |
| 5 | 18 | 27.111111 | 3.061931 |
| 6 | 23 | 33.888889 | 3.498725 |
| 7 | 50 | 40.666667 | 2.142077 |
| 8 | 三十六 | 33.888889 | 0.131512 |
| 9 | 三十七 | 27.111111 | 3.607013 |
| 10 | 二十七 | 20.333333 | 2.185792 |
| 11 | 14 | 13.555556 | 0.014572 |
| 12 | 7 | 6.777778 | 0.007286 |
| 全部的 | 244 | 244 | 16.889344 |
然后对卡方列求和。在本例中,和为 16.889344。这称为卡方统计量。“自由度”的数量比数据中的类别数少 1,在本例中为 11-1=10。最后,在统计表中查找 10.52 的卡方统计量,自由度为 10,或者在 Excel 中使用公式 =chidist(16.889344,10)。这两种方法都会得出 7.7% 的结果。这意味着公平骰子产生如此或更大偏差结果的概率是 7.7%。总而言之,虽然这些结果的偏差程度比预期的要大,但还没有严重到引起人们的怀疑。如果您继续进行此测试,我建议收集每个骰子的结果,而不是总和。还需注意的是,如果某一类别的预期结果数量较低,则卡方检验并不适用。最低预期值5是一个常见的数字。
如果掷骰子时两颗骰子点数相同,会发生什么情况?这算有效掷骰吗?如果有效,荷官会如何透露下方骰子点数是多少?
是否判定为有效掷骰取决于您所在地区。新泽西州博彩法规 19:47-1.9(a) 规定:
当其中一个或两个骰子离开桌面,或者一个骰子停在另一个骰子上面时,掷骰子无效。——新泽西州 19:47-1.9(a)
宾夕法尼亚州有完全相同的规定, 即第 537.9(a) 条:
当其中一个或两个骰子离开桌面,或者一个骰子停在另一个骰子上面时,掷骰子无效。——PA 537.9(a)
我问过一位拉斯维加斯的骰子荷官,他说如果掷骰子的结果在其他方面都正确,那么这就算有效掷骰。虽然他从未见过这种情况,但他表示,如果真的发生了,荷官会简单地移动顶部骰子,看看底部骰子落在哪个数字上。然而,人们可以在不触碰或查看顶部骰子的情况下判断底部骰子的结果。方法如下。首先,通过观察骰子的四个面,你可以将前面两种可能性缩小到两种。以下是如何根据这三种可能性进行判断。
- 1 或 6:寻找 3。如果高点与 5 相邻,则 1 位于上方。否则,如果高点与 2 相邻,则 6 位于上方。
- 2 或 5:寻找 3。如果高点与 6 相邻,则 2 位于上方。否则,如果高点与 1 相邻,则 5 位于上方。
- 3 或 4:寻找 2。如果高点与 6 相邻,则 3 位于上方。否则,如果高点与 1 相邻,则 4 位于上方。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
掷两个骰子,如果总数从 2 到 12 至少出现一次,则预期掷两次骰子的次数是多少?
这个问题是在 TwoPlusTwo.com 上提出的, BruceZ给出了正确的答案。以下解答与 BruceZ 的方法相同,值得称赞。答案比较难,请仔细阅读。
首先,考虑一下预期掷出 2 点的次数。掷出 2 点的概率是 1/36,所以平均需要掷 36 次才能掷出第一个 2 点。
接下来,考虑同时掷出 2 和 3 的预期次数。我们已经知道,平均需要掷 36 次才能掷出 2。如果在等待 2 的过程中掷出了 3,那么就不需要再掷 3 了。然而,如果没有,就需要掷更多次才能掷出 3。
掷出三的概率是 1/18,所以如果先掷出二,平均需要额外掷 18 次才能掷出三。假设掷出二的方法只有一种,掷出三的方法有两种,那么先掷出二的概率是 1/(1+2) = 1/3。
所以,有1/3的概率我们需要额外掷18次才能掷出3。因此,同时掷出2和3的预期次数为36+(1/3)×18 = 42。
接下来,考虑一下你还需要掷多少次才能掷出4。如果你掷出2和3的时候还没有掷出4,那么平均下来你还需要掷12次才能掷出1次。这是因为掷出4的概率是1/12。
那么,先得到四,再得到二和三的概率是多少呢?首先,让我们回顾一下当 A 和 B 不互斥时的一个常见概率规则:
pr(A 或 B) = pr(A) + pr(B) - pr(A 和 B)
你减去 pr(A 和 B),因为这个偶然性在 pr(A) + pr(B) 中被重复计算了。所以,
pr(2 或 3 之前 4) = pr(2 之前 4) + pr(3 之前 4) - pr(2 和 3 之前 4) = (3/4)+(3/5)-(3/6) = 0.85。
在掷出2和3的过程中,没有掷出4的概率是1.0 - 0.85 = 0.15。因此,需要额外掷12次的概率为15%。因此,掷出2、3和4的预期次数为42 + 0.15*12 = 43.8。
接下来,考虑一下你还需要掷多少次才能掷出5。当你掷出2到4的时候,如果你还没有掷出5,那么平均来说,你需要再掷9次才能掷出1,因为掷出5的概率是4/36 = 1/9。
在得到2、3或4之前得到5的概率是多少?一般规则是:
pr (A 或 B 或 C) = pr(A) + pr(B) + pr(C) - pr(A 和 B) - pr(A 和 C) - pr(B 和 C) + pr(A 和 B 和 C)
因此,pr(2 或 3 或 4 之前 5) = pr(2 之前 5)+pr(3 之前 5)+pr(4 之前 5)-pr(2 和 3 之前 5)-pr(2 和 4 之前 5)-pr(3 和 4 之前 5)+pr(2、3 和 4 之前 5) = (4/5)+(4/6)+(4/7)-(4/7)-(4/8)-(4/9)+(4/10) = 83/90。在从 2 到 4 的过程中没有掷出 4 的概率是 1 - 83/90 = 7/90。因此,有 7.78% 的可能性需要额外掷 7.2 次。因此,掷出 2、3、4 和 5 的预期次数是 43.8 + (7/90)*9 = 44.5。
继续用同样的逻辑,计算总数从 6 到 12 的概率。每次计算下一个数字作为最后一个数字之前的概率时,所需的计算次数大约翻倍。当总数达到 12 时,你将需要进行 1,023 次计算。
这是 pr(A 或 B 或 C 或 ... 或 Z) 的一般规则
pr(A 或 B 或 C 或 ... 或 Z) =
pr(A) + pr(B) + ... + pr(Z)
- pr (A 和 B) - pr(A 和 C) - ... - pr(Y 和 Z) 减去两个事件的每种组合的概率
+ pr (A and B and C) + pr(A and B and D) + ... + pr(X and Y and Z) 将三个事件的每种组合的概率相加
- pr (A 和 B 和 C 和 D) - pr(A 和 B 和 C 和 E) - ... - pr(W 和 X 和 Y 和 Z) 减去四个事件的每种组合的概率然后不断重复,记住奇数事件的概率加起来,偶数事件的概率减去。对于大量可能发生的事件,这显然会变得繁琐,实际上需要电子表格或计算机程序。
下表显示了每一步的预期点数。例如,掷出 2 需要掷 36 点,掷出 2 和 3 需要掷 42 点。右下角单元格显示掷出全部 11 个点数的预期次数为 61.217385。
预期掷骰次数问题
| 所需最高数量 | 可能性 | 如果需要的话,预期的卷 | 不需要概率 | 所需概率 | 预计总掷骰数 |
|---|---|---|---|---|---|
| 2 | 0.027778 | 36.0 | 0.000000 | 1.000000 | 36.000000 |
| 3 | 0.055556 | 18.0 | 0.666667 | 0.333333 | 42.000000 |
| 4 | 0.083333 | 12.0 | 0.850000 | 0.150000 | 43.800000 |
| 5 | 0.111111 | 9.0 | 0.922222 | 0.077778 | 44.500000 |
| 6 | 0.138889 | 7.2 | 0.956044 | 0.043956 | 44.816484 |
| 7 | 0.166667 | 6.0 | 0.973646 | 0.026354 | 44.974607 |
| 8 | 0.138889 | 7.2 | 0.962994 | 0.037006 | 45.241049 |
| 9 | 0.111111 | 9.0 | 0.944827 | 0.055173 | 45.737607 |
| 10 | 0.083333 | 12.0 | 0.911570 | 0.088430 | 46.798765 |
| 11 | 0.055556 | 18.0 | 0.843824 | 0.156176 | 49.609939 |
| 12 | 0.027778 | 36.0 | 0.677571 | 0.322429 | 61.217385 |
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
据Craps Advantage Players网站报道,拉斯维加斯的赌场经常使用加重骰子来增加七点的概率,从而增加利润。我简直不敢相信!巫师对此有何看法?
巫师说那个网站听起来满嘴胡言乱语,没有任何可信的证据来证明指控的合理性。如果我有证据,我很乐意揭露任何赌场使用有偏见的骰子。
如果有人有确凿的证据证明骰子存在偏差,我很乐意进行检验并发表我的结论。我希望看到的证据要么是掷骰子的日志文件,要么最好是一些实际存在的所谓偏差骰子。
此外,如果赌场确实使用的骰子产生的“七”的数量超过了预期,那么为什么这些侦探不知道赌“不通过”和下注赔率的阴谋呢?
老虎机上的“Hot Roll”奖励回合将根据两枚骰子的总点数奖励玩家以下数量的硬币。玩家持续收集硬币,直到掷出总点数“7”为止,奖励结束。如果第一次掷出“7”,他将获得70枚硬币的安慰奖。除“7”之外,其他所有点数的奖励如下:
- 2或12:1,000
- 3或11:600
- 4或10:400
- 5或9:300
- 6或8:200
我的问题是平均奖金是多少?
点击以下按钮查看答案。
答案是 1983.33。点击以下按钮获取解决方案。
[/spoiler] 设答案为 x。只要玩家没有掷出 7,他就能预期未来的胜率总是 x,加上之前的所有胜率。换句话说,掷骰子具有无记忆特性,即无论你已经掷出多少次,你都不会比开始时更接近 7。我不会深入讨论骰子概率的基础知识,但只是说每个总数的概率如下:
- 2:1/36
- 3:2/36
- 4:3/36
- 5:4/36
- 6:5/36
- 7:6/36
- 8:5/36
- 9:4/36
- 10:3/36
- 11:2/36
- 12:1/36
在考虑安慰奖之前,x 的值可以表示为:
x = (1/36)*(1000 + x) + (2/36)*(600 + x) + (3/36)*(400 + x) + (4/36)*(300 + x) + (5/36)*(200 + x) + (5/36)*(200 + x) + (4/36)*(300 + x) + (3/36)*(400 + x) + (2/36)*(600 + x) + (1/36)*(1000 + x)接下来,将两边乘以 36:
36x = (1000 + x) + 2*(600 + x) + 3*(400 + x) + 4*(300 + x) + 5*(200 + x) + 5*(200 + x) + 4*(300 + x) + 3*(400 + x) + 2*(600 + x) + (1000 + x)36倍=11,200+30倍
6倍=11,200
x = 11,200/6 = 1866.67。
接下来,安慰奖的价值是700*(6/36)=116.67。
因此,奖金的平均赢额为 1866.67 + 116.67 = 1983.33。
[/spoiler]


