请问巫师 #427
蛋糕按以下方式分割:
- 第一个人获得1%
- 第二个人获得剩余财产的2%。
- 第三个人获得剩余财产的3%。
- 等等。
谁能分到最多的蛋糕?禁止使用电子表格或穷举法计算。
【剧透=答案】第十个人将获得最多的蛋糕。【剧透结束】
这是我的解决方案(PDF)。
这个问题在我的Wizard of Vegas论坛上被提出和讨论过。
我要感谢“Mind Your Decisions” YouTube频道提供的这道数学谜题。
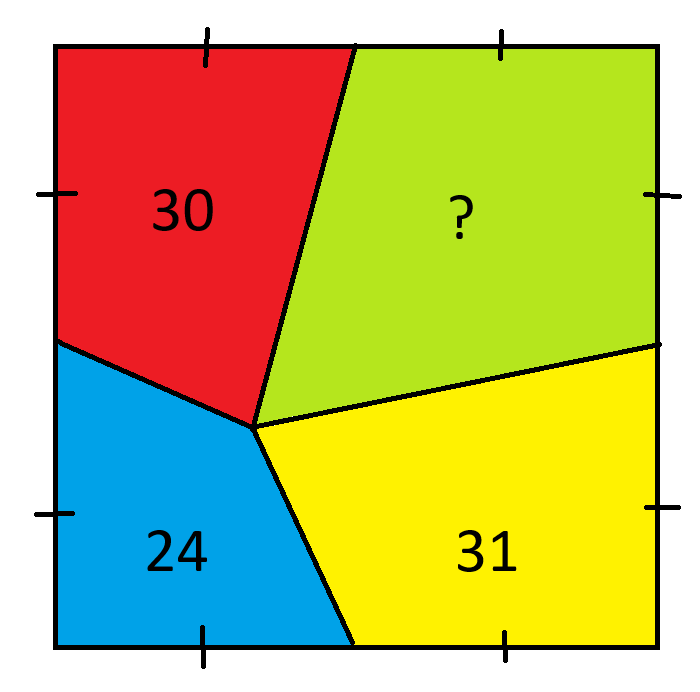
绿色区域的面积是多少?
首先,从四个图形的交点分别向四个角画四条线。然后按如下方式标记这八个图形。
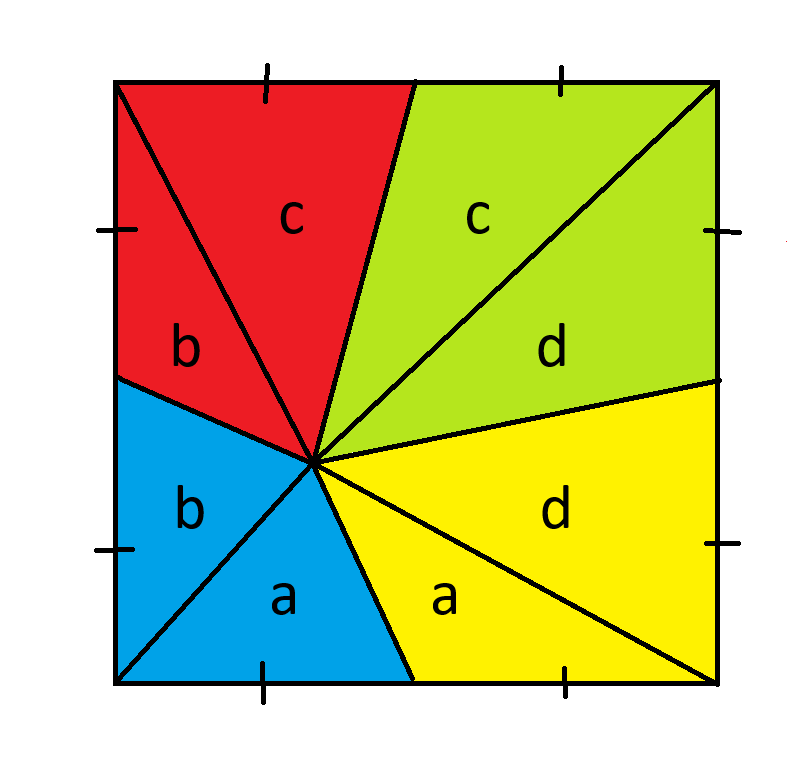
记住,三角形的面积公式是底乘以高除以2。由于所有三角形的底边都相同,我们可以认为高度相等的三角形面积也相等。
至此我们已知:
- (1)A+B=34
- (2)B+C = 42
- (3)A+D=30
将等式(2)和(3)相加:
A+B+C+D=72
让我们从中减去公式(1):
C+D=38,这就是我们的答案。
[剧透结束]这个问题曾在我的Wizard of Vegas论坛上被提出和讨论过。
这个谜题的来源是YouTube 视频“98% 的人解不出这道数学题”。
假设你想求几个值的平均值。你觉得像奥运会体操比赛那样去掉最高值和最低值怎么样?假设目的是求某个特定街区每平方英尺的平均值。
问得好。你说的这个叫做截尾均值。我不知道有什么统计量可以衡量截尾均值与真实均值之间的方差。由于没有更好的办法,我自己做了个实验。
为了回答你的问题,我抽取了 10 万个样本,每个样本包含 10 组数值。每个数值都服从标准正态分布,即均值为 0,方差为 1。然后,我计算了所有 10 个数值的均值,以及剔除部分数值后的 8 个数值的均值。
我发现,对所有十个值进行抽样,样本均值与真实均值之间的平均差异为 0.003450。同样地,如果取截尾均值的平均值,则平均差异为 0.003445。我认为,这种差异不足以判断哪种方法更好。此外,适用于我的实验的方法可能并不适用于其他应用场景。
总之,我很少这么说,但我没有确切的数学答案。
对于底面为正方形或三角形的球体,哪种堆叠方式效率更高(即最节省空间)?


我的回答方式是:当球体数量趋于无穷大时,哪个金字塔的球体体积与包围它们的金字塔体积之比最大。
这是我的解决方案(PDF)。
我后来发现这个问题在“问问魔法师”第350期中也有人问过。不过,我认为这个解决方案更好。


