请问巫师 #419
我注意到你没有任何关于连续皇家牌赔率更高的视频扑克策略。你能帮我吗?
首先,让我澄清一些视频扑克术语。
- 顺序皇家 = 仅从低到高 (10-JQKA)
- 可逆皇家 = 双向(10-JQKA 或 AKQJ-10)
更令人困惑的是,并非所有人都使用这个术语,而且如果游戏单独列出连续皇家的赔付项目,则可能双方都会获得赔付。希望规则界面能够澄清这一点。
话虽如此,玩一手可能出现顺子或可逆皇家的牌,最简单完美的方法就是把它输入我的视频扑克计算器。链接如下:
如果您不能或不想在机器上使用我的网站,请注意,当可逆皇家牌根据已经到位的牌数为 5 个信用点的赌注支付 50,000 时,皇家牌的平均胜利数额。
- 4 至可逆皇家 = 10,000
- 3 至可逆皇家 = 5,400
- 2 至可逆皇家 = 2,333
- 1 至可逆皇家(中间位置)= 1,567
- 1 至可逆皇室(非中间位置)= 1,183
- 0 到可逆皇家 = 800
对于连续皇家游戏(仅支付从低到高的赔率),无论位置如何,都使用 1,183 这个数字。
有了这些数据,使用我的视频扑克策略制定器,为每张平均皇家牌获胜次数创建单独的策略。然后根据皇家牌正确位置的数量,在机器上使用该策略。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
家乐氏推出了新款球形苹果杰克、糖霜薄片和克雷夫,他们声称这种形状能带来更浓郁的糖霜。事实上,他们说“我们算过了”。他们算对了吗?

不!不!他们的计算方法不对。事实上,如果要最大化表面积与体积的比值,球体是最糟糕的三维形状。
让我们首先看一下盒子背面的表面积方程。

他们确实正确地指出了球体(或者他们可能称之为甜甜圈洞)的表面积是 4πr 2 ,其中 r=半径。
然而,他们错误地将圆环(他们可能称之为甜甜圈)的表面积表示为 2π 2 rR。实际公式是其两倍,即 4π 2 rR。请参考下图中 r 和 R 的表达式。
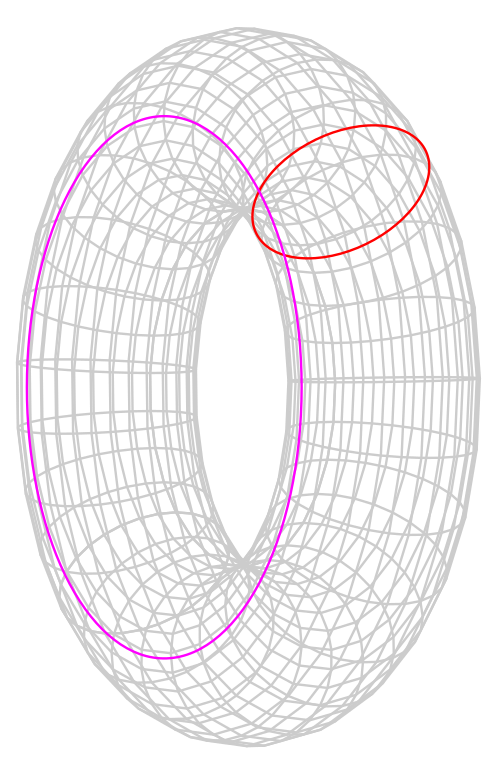
r = 红色圆圈的半径
R = 圆环最近部分到中心的距离。
图片来源:维基百科关于环面的页面。
你可能会说,球形的替代品就像在甜甜圈上抹糖霜一样,只在半个圆环上涂釉。然而,我仔细观察了一款圆环状的传统苹果杰克,发现它们在整个圆环上都涂了釉。
为了说明我的下一个观点,我还想提供球体和圆环的体积公式。
- 球面 = (4/3)πr 3
- 环面 = 2π 2 r 2 R
提醒一下,表面积的公式是体积的导数。
对于 r=1 且 R=1 的环面,我们得到其表面积为 39.478418,体积为 19.739209。有趣的是,表面积与体积之比,或者说釉面比,恰好是 2。
为了使体积相等,球体的半径必须是1.676539。对于该球体的半径,我们得到表面积为35.321350,体积为19.739209。表面积与体积的比值,或称釉面比,为1.789400。
换句话说,圆环在相同体积下可提供更大的表面积或釉料。
我之前提到过,如果目标是最大化表面积与体积的比值,那么球形是最糟糕的三维形状。这被称为等周不等式。虽然这已经被证明,但我认为它是不言而喻的。例如,气泡会努力最小化表面积并最大化强度,而它们的形状就是球形的。
关键是,如果你想要减少糖霜,而不是增加糖霜,你应该买球形或甜甜圈形状的苹果杰克或其他任何形状的。这正是我的目标,因为我觉得这些麦片太甜了,希望糖霜少一点。我还强烈谴责家乐氏的虚假广告,他们因此受到了巫师们罕见的谴责。
这个问题是在我的“拉斯维加斯巫师”论坛上提出并讨论的。
欲了解更多信息,我推荐观看 MindYourDecisions 频道的 Presh Talwalkar 制作的 YouTube 视频“ Internet spot big mistake on Kellogg's cereal box” (我的最爱之一!)。
视频扑克中发出一手牌获胜的概率是多少?
我可以看到这个问题的答案在某些视频扑克变体中具有实际应用,如果玩家在交易中取得胜利,这些变体会提供奖励功能。
答案取决于视频扑克的格式。下表显示了视频扑克中52张牌(不含百搭牌)发牌时所有可能事件的组合数和概率,从赔率最低的一对J开始。
| 手 | 组合 | 可能性 |
|---|---|---|
| 皇家同花顺 | 4 | 0.000002 |
| 同花顺 | 三十六 | 0.000014 |
| 四条 | 624 | 0.000240 |
| 客满 | 3,744 | 0.001441 |
| 冲洗 | 5,108 | 0.001965 |
| 直的 | 10,200 | 0.003925 |
| 三条 | 54,912 | 0.021128 |
| 两对 | 123,552 | 0.047539 |
| 杰克或更好 | 337,920 | 0.130021 |
| 所有其他 | 2,062,860 | 0.793725 |
| 全部的 | 2,598,960 | 1.000000 |
在杰克或更好的视频扑克游戏中,任何获胜牌的概率为 0.206275。
第二个表格显示了视频扑克中所有可能事件的组合数和概率,该扑克牌有 52 张牌,其中 2 为百搭牌,从三张同点牌的最低赔付牌开始。
| 手 | 组合 | 可能性 |
|---|---|---|
| 天然皇家同花顺 | 4 | 0.000002 |
| 四张 2 | 四十八 | 0.000018 |
| 狂野皇家同花顺 | 480 | 0.000185 |
| 五张同点牌 | 624 | 0.000240 |
| 同花顺 | 2,068 | 0.000796 |
| 四条 | 31,552 | 0.012140 |
| 客满 | 12,672 | 0.004876 |
| 冲洗 | 14,472 | 0.005568 |
| 直的 | 62,232 | 0.023945 |
| 三条 | 355,080 | 0.136624 |
| 所有其他 | 2,119,728 | 0.815606 |
| 全部的 | 2,598,960 | 1.000000 |
在 Deuces Wild 视频扑克游戏中,任何一手牌获胜的概率为 0.184394。
第三张表显示了视频扑克中 53 张牌(包括一张鬼牌)发牌时所有可能事件的组合数和概率,从一对 K 的最低赔率牌开始。
| 手 | 组合 | 可能性 |
|---|---|---|
| 五条 | 十三 | 0.000005 |
| 皇家同花顺 | 24 | 0.000008 |
| 同花顺 | 180 | 0.000063 |
| 四条 | 3,120 | 0.001087 |
| 客满 | 6,552 | 0.002283 |
| 冲洗 | 7,804 | 0.002719 |
| 直的 | 20,532 | 0.007155 |
| 三条 | 137,280 | 0.047838 |
| 2对 | 123,552 | 0.043054 |
| 国王或更好 | 262,956 | 0.091632 |
| 所有其他 | 2,307,672 | 0.804155 |
| 全部的 | 2,869,685 | 1.000000 |
在小丑扑克(国王或更好)视频扑克游戏中,任何一手获胜的概率为 0.195845。


