请问巫师 #413
有没有什么方法可以进行满足以下要求的秘密圣诞礼物交换:
- 没有人会给自己送礼物。
- 沒有重来。
- 除了知道要为谁买东西之外,没有人知道其他任何事情。
- 每场比赛都有同等的可能性。
是的!我把以下方法称为 Hannah Fry 方法。
- 制作一组如下所示的卡片。每张卡片的顶部和底部都应有一个唯一的数字。在下面的例子中,数字是 23。
- 洗牌并重新堆叠。
- 保持卡片堆完好无损,沿着中间的线剪开每张卡片,形成两叠。
- 切割并完成其中一个堆栈的切割。
- 将每堆卡片最上面的一张逐一分发给每个参与者。
- 创建一个编号列表并要求每个人都在上面写下他们的编号。
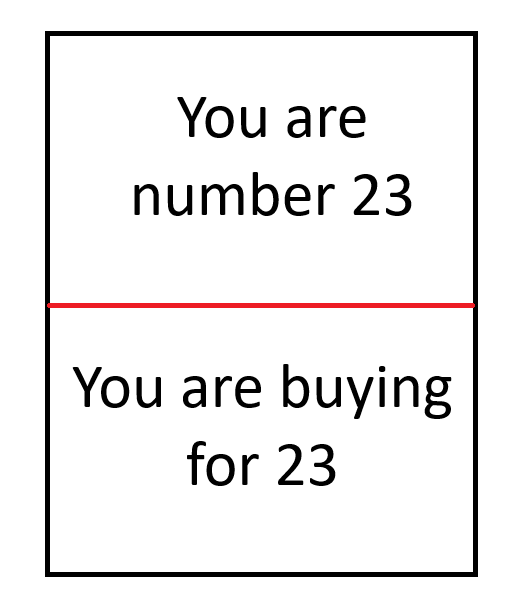
完成此程序后,每个人都会得到两张卡片,例如,上面写着“您是 13 号”和“您要为 7 号购买”。一旦列表填写完毕,每个人都知道要为谁购买,但不知道谁会为他们购买。
一个游泳池里充满了盐水。游泳池可容纳1000立方米的水。一根花园软管以每小时1立方米的速度将淡水注入游泳池。当淡水流入时,水以相同的速度从另一端流出。游泳池需要多长时间才能只剩下1%的盐水?
答案是 2000 ln(10) =~ 4605.170186 小时 =~ 191.8821 天。
这是我的解决方案(PDF)。
平均而言,每个柏拉图立体需要滚动多少次才能滚动到之前滚动过的任意一面?
图片来源:维基百科
这是按边数计算的答案。
| 侧面 | 平均卷数 |
|---|---|
| 4 | 3.218750 |
| 6 | 3.774691 |
| 8 | 3.846558 |
| 12 | 5.036074 |
| 20 | 6.293585 |
让我们来计算一下六面立方体的情况。
- 实验以两次掷骰子结束的概率是 1/6。
- 实验以三次掷骰子结束的概率是 (5/6)*(2/6)。
- 实验以四次掷骰子结束的概率是 (5/6)*(4/6)*(3/6)。
- 实验以五次掷骰子结束的概率是 (5/6)*(4/6)*(3/6)*(4/6)。
- 实验以六次掷骰子结束的概率是 (5/6)*(4/6)*(3/6)*(2/6)*(5/6)。
- 实验以七次投掷结束的概率是 (5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6)。
设 pr(n) = 实验在 n 次滚动后结束的概率。
预期掷出的点数为:2*pr(2) + 3*pr(3) + 4*pr(4) + 5*pr(5) + 6*pr(6) + 7*pr(7) =
2*(1/6) + 3*(5/6)*(2/6) + 4*(5/6)*(4/6)*(3/6) + 5*(5/6)*(4/6)*(3/6)*(4/6) + 6*(5/6)*(4/6)*(3/6)*(2/6)*(5/6) + 7*(5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6) =~ 3.774691358。


