请问巫师 #412
在百家乐中,一副牌中一方(庄家或闲家)出现的次数至少是另一方的三倍的概率是多少?
如果我只是对此做一个估计,请原谅我。
平均每副牌有80.88手牌。平均7.70手牌为平局,庄家和闲家合计赢73.18手。如果一方的赢率是另一方的3倍,则需要出现54.89次,另一方需要出现18.30次。
在已结算的73.18个投注中,我们预计庄家赢37.09次,闲家赢36.09次。两者的标准差均为4.28。要达到54.89次或更高的赢率,庄家赢4.16个标准差,闲家赢4.39个标准差。任何一方赢这么多标准差的概率约为47,000分之一。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
以下是2028年总统大选获胜者的投注赔率。其他人获胜的概率是多少?
| 赌注 | 支付 |
|---|---|
| 万斯 | +250 |
| 纽瑟姆 | +750 |
| 夏皮罗 | +900 |
| 奥巴马 | +1200 |
| 布蒂吉格 | +1400 |
| 惠特默 | +1600 |
| 拉马斯瓦米 | +1600 |
| 德桑蒂斯 | +2000 |
像这样的未来投注,赌场优势通常约为 30%。如果我们假设在 -160 的赔率下注,那么所有投注的赌场优势将达到 29.95%。下表显示了详细信息。“隐含概率”表示投注完全公平时的概率。“实际概率”是每个投注的公平概率除以所有公平概率之和。这表明其他人获胜的概率为 43.1%。
| 赌注 | 支付 | 暗示 可能性 | 实际的 可能性 |
|---|---|---|---|
| 万斯 | +250 | 0.285714 | 0.200136 |
| 纽瑟姆 | +750 | 0.117647 | 0.082409 |
| 夏皮罗 | +900 | 0.100000 | 0.070048 |
| 奥巴马 | +1200 | 0.076923 | 0.053883 |
| 布蒂吉格 | +1400 | 0.066667 | 0.046698 |
| 惠特默 | +1600 | 0.058824 | 0.041204 |
| 拉马斯瓦米 | +1600 | 0.058824 | 0.041204 |
| 德桑蒂斯 | +2000 | 0.047619 | 0.033356 |
| 场地 | -160 | 0.615385 | 0.431062 |
| 全部的 | 1.427602 | 1.000000 |
总回报率是隐含概率之和的倒数,即 1/1.427602 =~ 0.700475。回报率与庄家优势之和为 1,因此庄家优势为 1.000000 - 0.700475 = 0.299524。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
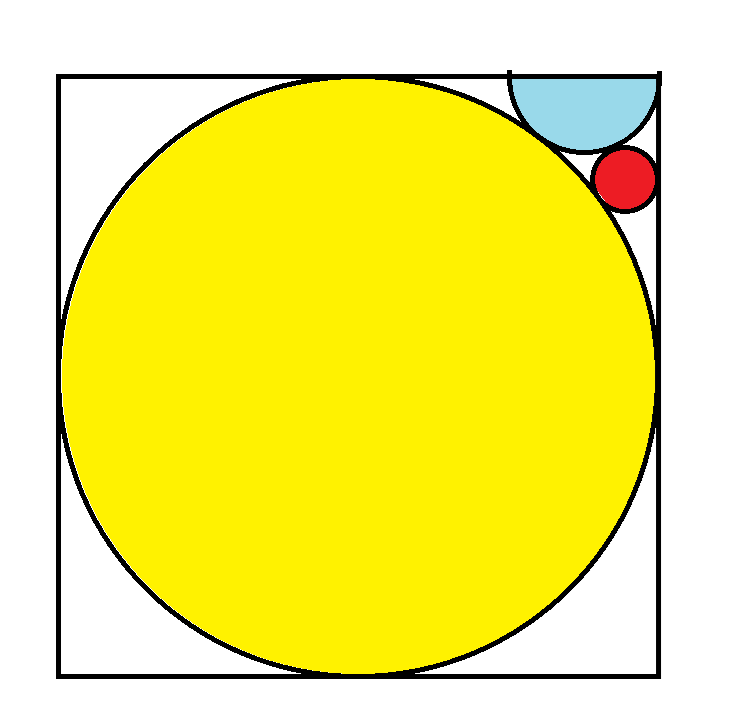
下图中,黄色圆圈的半径为1,红色圆圈的面积是多少?