请问巫师 #410
我看到您在“问问巫师”专栏第115期“价格猜猜猜”栏目中回答了一个关于Plinko游戏的问题。不过,他们有时会根据特殊节目调整奖金数额。例如,在“巨额奖金周”节目中,奖金从左到右依次为500美元、1000美元、2500美元、0美元、200000美元、0美元、2500美元、1000美元、500美元。那么,冰球从哪个位置落下的预期价值是多少?在给定的起始位置,冰球落入任意指定奖品的概率是多少?
冰球的起始位置有九个。不过,我们只需要关注其中五个,因为奖品和棋子布局是对称的。让我们从左边缘开始,依次从1到5标记它们。
还有九个结束位置,让我们从左边开始,将前五个标记为 1 到 5。

下表显示了根据掉落位置(顶行)落在任何给定位置(左列)的概率。
| 着陆点 | 掉落 1 或 9 | 掉落 2 或 8 | 掉落 3 或 7 | 掉落 4 或 6 | 掉落 5 |
|---|---|---|---|---|---|
| 1 或 9 | 0.225586 | 0.193359 | 0.121094 | 0.056641 | 0.032227 |
| 2 或 8 | 0.386719 | 0.346680 | 0.250000 | 0.153320 | 0.113281 |
| 3 或 7 | 0.242188 | 0.250000 | 0.257813 | 0.250000 | 0.242188 |
| 4或6 | 0.113281 | 0.153320 | 0.250000 | 0.346680 | 0.386719 |
| 5 | 0.032227 | 0.056641 | 0.121094 | 0.193359 | 0.225586 |
| 全部的 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
下表显示了您询问的“巨额奖金周”中各个投掷位置的预期价值。不出所料,玩家应该投掷冰球方向,以获得最高奖金。
| 投放地点 | 预期胜利 |
|---|---|
| 1 或 9 | 7,550.29 美元 |
| 2 或 8 | 12,396.48 美元 |
| 3 或 7 | 25,173.83 美元 |
| 4或6 | 39,478.52 美元 |
| 5 | 45,852.05 美元 |
加布里埃尔号角悖论是什么?
首先考虑由方程 y=1/x 得到的曲线,其中 x 的取值范围为 1 到无穷大。当 x 的取值范围达到 17 时,该曲线将如下所示。
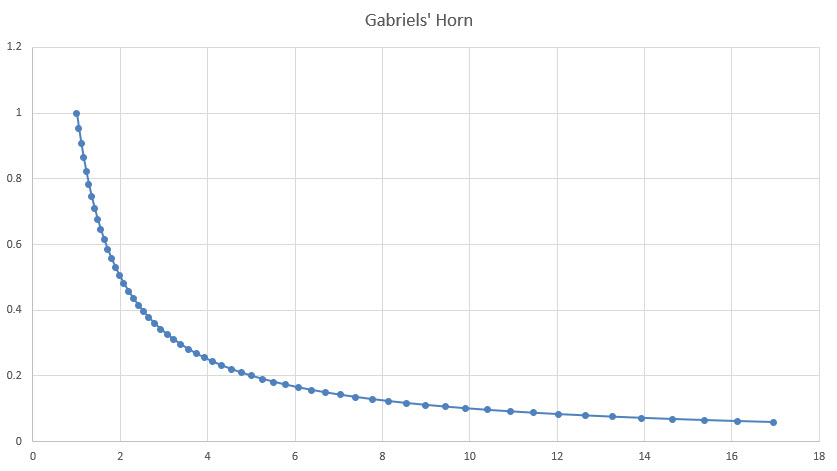
接下来,想象一下这条曲线绕着 x 轴旋转。它会形成一个像号角一样的形状,末端无限长。这就是数学家所说的加布里埃尔号角?

图片来源:数学之魂。
接下来,考虑一下有关加百列号角的问题:
- 音量是多少?
- 表面积是多少?
以下是答案:
- 体积 = π = pi。
- 表面积=无穷大
您可以在此处(PDF)找到我展示这些问题答案的作品。
这个悖论的本质是:体积怎么会是有限的,而表面积却无限呢?
当我们混淆二维和三维时,就会出现这种可感知的悖论。我们不应该这样做。考虑半径为 1 的圆 A 和半径为 1.1 的圆 B,其中圆 A 位于圆 B 内。
圆 A 的周长为 2*pi =~= 6.283185,圆 B 的面积为 1.1^2 * pi =~ 3.801327。请注意,圆 B 比圆 A 大,但其面积小于圆 B 的周长。这并不意味着圆 B 的周长是圆 A 面积的一部分。面积和周长是不同维度上的不同测量值,不应进行比较。
另一种看待这个问题的方式是,如果我们用圆圈 A 制作一张具有无限多个凹槽的唱片,那么这些凹槽的长度将是无限的。
回到加百利号角,考虑将其简化为半径为 1、1/2、1/3、1/4 的圆的离散情况......
这些圆的体积之和为 pi*(1/1 + 1/4 + 1/9 + 1/16 + ...)。有一个著名的无穷级数:
1/1 + 1/4 + 1/9 + 1/16 + ... = pi^2/6 =~ 1.644934。
再添加一个 pi 项,圆的面积之和为 pi^3/6 =~ 5.167713。
同时,圆周长之和为 2*pi(1/1 + 1/2 + 1/3 + 1/4 + ...)。
数学中另一个著名的无穷级数称为调和级数,其含义为:
1/1 + 1/2 + 1/3 + 1/4 + ... = ∞ = 无穷大。
2*pi*∞ 仍然等于 ∞。
如果我们将这个逻辑扩展到圆圈之间无限小的距离,我们就会得到加百利号角。
内森买了100磅豆子。这些豆子的重量中99%是水。她把它们放在阳光下晒干。第二天,她发现这些豆子的重量是98%。它们现在的重量是多少?
让:
- w = 原始水重量。
- w' = 豆子干燥后的水分重量。
- x = 豆子中其他所有物质的重量。
第一天我们得到:
w + x = 100
瓦/(瓦+x) = 0.99
将第一个方程代入第二个方程:
含100 = 0.99
w = 99
因此,x=1。
第二天,我们得到:
w'/(w'+x) = 0.98
w' = 0.98*(w'+x)
0.02w' = 0.98x
我们知道 x=1 所以:
0.02w' = 0.98
w' = 0.98/0.02 = 49
第二天的总重量为x+w'=1+49=50。
[/spoiler]


