请问巫师 #405
x 2 - 3 = sqrt(x+3)。解出 x。
令 y = 两个表达式。因此,我们有:
- y = x^2 - 3
- y = 平方根(x + 3)
注意两个表达式中的 3。让我们将两个等式都表示为一边带 3。首先我们有:
3 = x^2 - y
接下来,让我们对上面的第二个方程求平方:
y^2 = x+3
3 = y^2 - x
让我们将 3 的两个表达式相等:
x^2 - y = y^2 - x
让我们重新排列一下:
x^2 - y^2 + x - y = 0
(x+y)(xy) + x - y = 0
(xy)(x+y+1) = 0
首先让我们检查 xy = 0:
xy = 0
让我们用 y = x^2 - 3 代替 y。
x - (x^2 - 3) = 0
x^2 - x - 3 = 0
使用勾股定理公式:
x = (1 +/- 平方根(1 + 12)/2
x = (1 + sqrt(13)/2 & x = (1 - sqrt(13)/2
其次,让我们检查 x+y+1 = 0:
让我们用 y = x^2 - 3 代替 y。
x + (x^2 - 3) + 1 = 0
x + x^2 - 3 + 1 = 0
x^2 + x - 2 = 0
使用勾股定理公式:
x = (-1 +/- 平方根(1 + 8)/2
x = (-1 +/- 3)/2
x = 1, x = -2
因此,我们的四个答案是:
- x = 1
- x = -2
- x = (1 + sqrt(13)/2 =~ 2.302776
- x = (1 - sqrt(13)/2 =~ -1.302776
感谢 SyberMath 的 YouTube 视频“求解 x^2-3=sqrt(x+3)”提供了这个解题方法。请跳转至 6:28 处查看此方法。
半径为 1 的圆外一点可以看到圆周的 1/3。该点距离圆有多远?
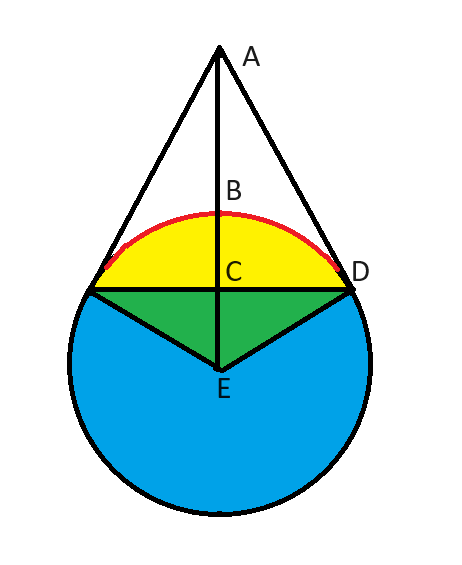
考虑三角形ADE。我们知道:
- 角ADE为90度,因为AD与圆相切。
- 角 AED 为 60 度,因为 E 处的绿色三角形角为 120 度(整个 360 度的 1/3)。
- 角 EAD 必定是三角形 ADE 的另外 30 度。
这是经典的 30-60-90 三角形。我们都知道,这个三角形的边长分别与 1、2 和 sqrt(3) 成比例。
在这种情况下,ED = 1,正如问题中给出的。AE 是该距离的两倍,即 2。
2 给出的是该点到圆心的距离。我们被要求计算该点到圆上最近点的距离。因此,我们减去半径。因此,答案是 2-1 = 1。
鲍勃和汤姆正走过一座火车桥,距离出发点还有三分之一的路程。这时,他们听到身后驶来一列火车。两人都能以每小时5英里的速度奔跑。鲍勃转身,汤姆向前跑去。两人都与火车擦肩而过,只差不到一秒。火车的速度是多少?
记住距离 = 速率 * 时间,我们将其表示为 d = r * t
重写为:t = d/r。
鲍勃和火车在桥的起点相遇的时间是相同的:
让我们:
- x = 火车最初与桥梁起点之间的距离。
- r = 火车速度
首先,我们来看看跑回来的鲍勃。我们来表示一下鲍勃和火车在桥头相遇的时间 t:
鲍勃:t = (1/3)/5
训练:t = x/r
将 t 的两个表达式相等:
(1/3)/5 = x/rr/3 = 5倍
r = 15x
其次,我们来看看汤姆,他跑在前面。我们把汤姆和火车在桥头相遇的时间t表示为:
汤姆:t = (2/3)/5
训练:t = (1+x)/r
将 t 的两个表达式相等:
(2/3)/5 = (1 + x)/ r
2r/3 = 5(1+x)
2r = 15(1+x)
2r = 15 + 15x
此时我们有:
- r = 15x
- 2r = 15 + 15x
我们将第一个方程中 r 的表达式代入第二个方程中:
30倍=15+15倍
15x = 15
x = 1
回想一下,r = 15x。
因此,火车的速度为 15*1 = 15 英里/小时。


