请问巫师 #399
如果你从第一张图片中取出小正方形,并重新排列各个部分,总面积似乎仍然相同。这是怎么回事?
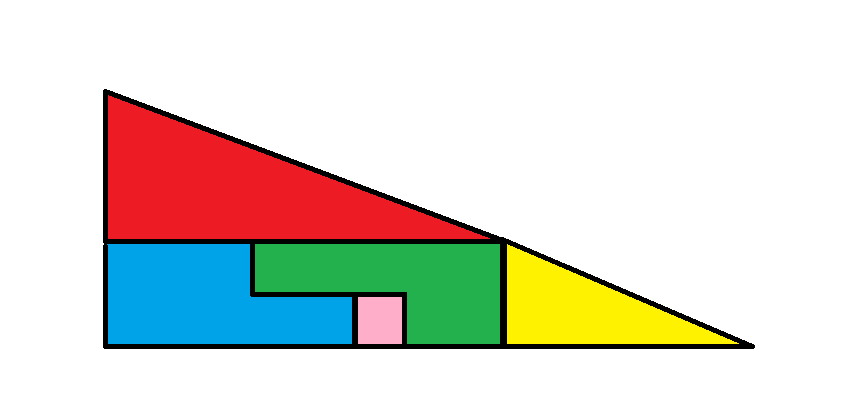
图 1
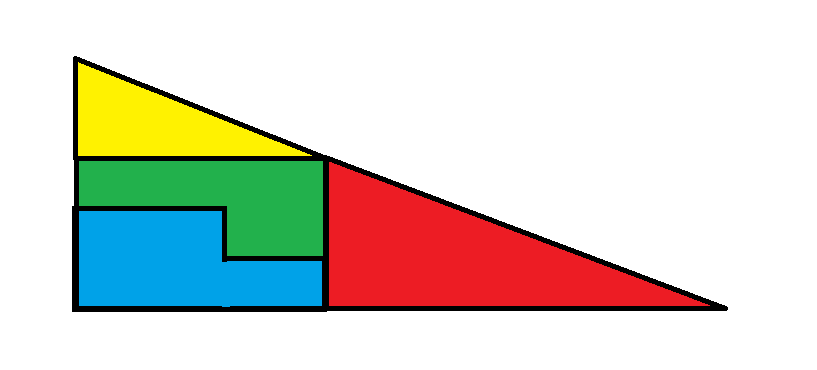
图 2
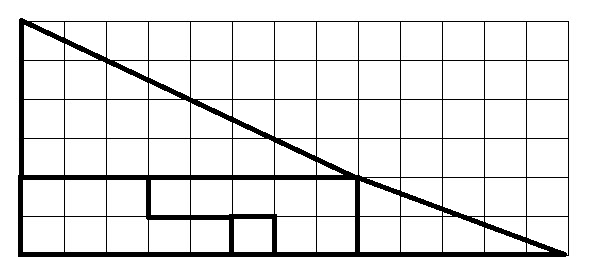
上图显示了网格上的第一个图像,以便更好地查看每个部分的大小。
请注意,大红色三角形的边长分别为4和8。接下来请注意,较小的黄色三角形的边长分别为2和5。换句话说,这两个三角形不成比例。两个三角形的斜边的斜率与图中所示不同。一个斜率为0.5,另一个斜率为0.4。按照图中所示的方式摆放这些碎片,看起来就像是一个边长分别为5和13的大三角形,但实际上它并不是一个真正的三角形。
红色三角形的面积为4*8/2=16。
黄色三角形的面积为2*5/2 = 5。
在第一幅图中,另外三块组成一个 2 x 8 的矩形,总面积为 16。
在第二幅图中,另外两块组成一个 3 x 5 的矩形,总面积为 15。
第一张图片的总面积是红色三角形+黄色三角形+大矩形=16+5+16=37。
第二幅图的总面积为红色三角形+黄色三角形+小矩形=16+5+15=36。
总而言之,第一幅图的正方形较小,但尺寸较大。这两种情况下,所有碎片组合在一起形成一个大三角形,这是一种视觉错觉。但事实并非如此。
一片大沙漠的边缘有16辆摩托车。每辆摩托车一箱油可以行驶100英里。所有摩托车都是满油状态出发。摩托车之间可以换油。目标是让一辆摩托车尽可能远离出发点。它能跑多远?
问题的关键是让队伍行驶一小段距离,然后把其中一辆摩托车剩余的汽油加满,再把其他摩托车的油箱加满。
例如,一开始将一箱油分成16份,每辆摩托车一份。然后大家一起骑,直到油箱消耗了1/16,这样全队就能跑100/16=6.25英里。从一辆摩托车中取出15/16的油,再将1/16的油抽到其他15辆摩托车中,这样就能恰好把油加满。
然后重复同样的过程,但剩下15辆摩托车,行驶1/15油箱所能行驶的距离,即100/15 = 6.666667英里。然后从一辆摩托车上取下另外14/15油箱的油,并将1/15油箱的油虹吸到另外14辆摩托车上。
继续这个过程,最后一辆摩托车的总距离将为 (1/16) + (1/15) + (1/14) + ... + (1/1) =~ 338.072899 英里。
[/spoiler]这个问题是在我的Wizard of Vegas论坛中提出并讨论的。
您对睡美人悖论有何看法?
为了其他读者的利益,以下是睡美人问题/悖论中所提出的问题。
睡美人(SB)自愿参加一项实验。实验的所有细节都如实向她解释如下:
- 星期日:SB 被安乐死。她睡着后,将抛一枚公平的硬币。
- 星期一:SB 将于星期一被叫醒并被问到“硬币正面朝上的概率是多少?”在她回答之后,她将被注射健忘症药物,让她再次陷入睡眠,忘记星期一发生的一切。
- 星期二:如果硬币反面朝上,周一的事情就会再次发生。如果硬币正面朝上,她就会睡一整天。
- 星期三:SB 再次被唤醒,什么也没问,实验结束后就回家了。
问题是她应该如何回答周一甚至周二提出的问题?
我的回答
如果这个实验重复一百万次,我们预计会看到三种类型的觉醒,每种类型的发生概率相同:
- 硬币落地正面,周一醒来。
- 硬币落在反面,周一醒来。
- 硬币落在反面,周二醒来。
这是因为周一醒来的次数应该在抛硬币正面和反面时均等分配。此外,如果硬币反面朝上,那么周一和周二醒来的次数将完全相同。因此,在较大的样本量下,三组醒来的次数大致相同。
在这些醒来的事件中,三分之一发生在抛硬币正面之后。因此,硬币正面朝上的概率是1/3。
1/2 阵营认为,SB 在每次醒来时都不会获得任何额外信息,因此应该假设翻转的每个结果都是同样可能的。
为此,如果硬币正面朝上,我会把这个问题扩展到999,999次唤醒。只有百万分之一的唤醒发生在抛硬币正面朝上之后。所以,很容易假设任何一次唤醒,都可能是抛硬币反面朝上之后999,999次唤醒中的一次。换句话说,在这种情况下,正确答案是百万分之一。
再扩展一下,如果让SB预测每次醒来时抛硬币的结果会怎样?如果她猜对了,她将赢得1000美元。如果她预测“正面”,她可以预期赢得(1/2)*1000=500美元。如果她预测“反面”,她可以预期赢得(1/2)*2000=1000美元。所以,SB被唤醒本身就有利于硬币抛向反面。
如果我的解释不清楚,维基百科上的“睡美人问题”比我更深入地探讨了这个问题,包括 SB 的其他可能的回应。
这个问题是在我的Wizard of Vegas论坛中提出并讨论的。


