请问巫师 #391
1 2 + 2 2 + 3 2 + ... + n 2 = ?
[spoiler=答案]1 2 + 2 2 + 3 2 + ... + n 2 = n(n+1)(2n+1)/6 [/剧透]
这是我的解决方案。(PDF)
假设你抛一枚公平硬币一百万次。仅使用一个带有五种基本算术函数(+、0、*、/、^)的简单计算器,抛出正面和反面次数完全相同的概率是多少?一个近似的估计就足够了。
回想一下标准正态曲线的方程:
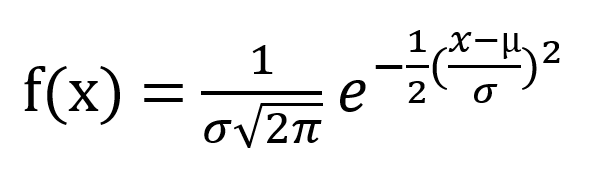
一次抛掷中反面次数的期望值为 0.5,反面次数的期望平方也为 0.5。因此,一次抛掷中反面次数的方差为 0.5 - (0.5) 2 = 0.5 - 0.25 = 0.25。一百万次抛掷的方差为 1,000,000 * 0.25 = 250,000。一百万次抛掷的标准差是该方差的平方根:sqrt(250,000) = 5,000。
设 x = 预期数量 500,000 的反面数。x 的均值为零。如图所示,x 的标准差为 5,000。
因此 x=0 的概率为:
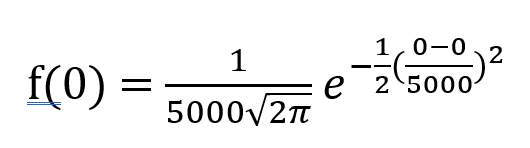
这简化为 1/(5000*sqrt(2*π)) =~ 0.000797885 =~ 1 in 1253.314137。
[/spoiler]链接
维基百科关于标准正态曲线的条目。
你正以 15 英里/小时的速度沿着一条健身路径骑自行车。路径上有一些慢跑者,速度为 5 英里/小时。每个方向的慢跑者数量相等。你遇到的慢跑者中,有多少比例会与你反方向行驶?
假设该路径长 15 英里。
骑自行车的人会在我开始前 3 小时到开始后 1 小时的任何时间遇到从另一侧开始的慢跑者,总共遇到 4 小时的慢跑者。
沿着同一方向,骑自行车的人会遇到比我早 2 小时或同时出发的慢跑者,总共 2 个小时。
因此,反方向慢跑的人数将是反方向慢跑人数的两倍。反方向慢跑的人数与所有慢跑人数的比例为4/(2+4) = 2/3。
相对于同方向的慢跑者,您的速度为 15-5 = 10 英里/小时。
相对于反方向的慢跑者,您的速度为 15+5 = 20 英里/小时。
因此,你遇到的反方向慢跑者数量是你的两倍。因此,比例为 2/(1+2) = 2/3。
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。


