请问巫师 #355
在电影《杀人执照》中,詹姆斯·邦德玩了三轮二十一点,每次玩五手。我注意到他一次都没中过牌。这几率是多少?
您可以在YouTube上找到该场景的片段。
游戏中确实出现了大量可疑的大牌,不是吗?以下是我能辨认出的牌。请注意,在某些情况下,牌可能看不清楚。
杀人执照——观察等级
| 秩 | 观察到 |
|---|---|
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 2 |
| 6 | 2 |
| 7 | 1 |
| 8 | 4 |
| 9 | 4 |
| 10 | 8 |
| J | 3 |
| 问 | 6 |
| 钾 | 4 |
| 一个 | 1 |
| 全部的 | 三十五 |
你说得对,邦德最初的15手牌一手都没要到。他分了一次8,但分完之后也没要到。以下是他最初15手牌的行动统计:
- 双倍 — 1
- 分裂 — 1
- 站立 — 13
以下是每个初始行动的基本策略概率,假设有六副牌,允许分牌后加倍,发牌人偷看底牌,并且发牌人在软 17 点停牌。
二十一点——首次行动概率
| 行动 | 可能性 |
|---|---|
| 站立 | 43.46% |
| 打 | 39.78% |
| 双倍的 | 9.53% |
| 分裂 | 2.48% |
| 二十一点 | 4.75% |
| 全部的 | 100.00% |
如果允许投降,那么这个概率就是 4.14%,这是从站立的概率中得出的。
值得注意的是,邦德曾经在16对10的情况下停牌。基本策略是击中它,但可能性很小。考虑到那手牌中出现了大量的10,邦德可能知道点数很高,这会触发基本策略例外,在这种情况下停牌。
一手牌没中概率是 60.22%。假设每手牌都是独立的,那么 15 手牌中 15 手牌没中概率是 0.602162 15 = 0.000496253 = 大约 2015 年的 1 手牌。
在《鱿鱼游戏》中,16 位玩家要通过一座玻璃桥进行游戏。这座桥被分成 18 块玻璃。每块玻璃中,一块是钢化玻璃,可以支撑一名玩家的重量。另一块是普通玻璃,会在玩家的重量下破碎。如果玩家踩到一块普通玻璃,就会破碎并坠落身亡。
玩家必须按照预先指定的顺序逐一前进。
假设随机猜测每对玻璃台阶,预计有多少玩家可以安全通过?
我会将答案和解决方案放在剧透标签中,以便让全世界的人都能自己找到答案。
[剧透=解决方案]
玩家 1 安全过关的概率是 (1/2)^18 = 1/262144 = 约 0.000004。
玩家 2 可以通过两种方式安全穿越:
- 玩家 1 安全过关。在这种情况下,玩家 2 只需复制他的步骤即可。
- 在玩家 1 和玩家 2 之间,只有一个错误步骤。这个错误步骤可能出现在 18 对可能的玻璃杯中。17 个正确步骤和 1 个错误步骤的概率是 18*(1/2)^2 = 18/262144 = 0.000069。
因此,球员 2 安全传球的概率为 0.000004 + 0.000069 = 0.000072。
玩家 3 可以通过两种方式安全过河:
- 玩家 2 安全过关。在这种情况下,玩家 3 只需复制他的步骤即可。
- 在玩家 1、2 和 3 之间,只有两个坏步骤。从 18 对玻璃中选出 2 个杀死玩家 1 和 2 的玻璃片,一共有 (18,2)=153 种方法。16 个好步骤和 2 个坏步骤的概率为 153*(1/2)^2 = 153/262144 = 0.000584。
因此,球员 3 安全传球的概率为 0.000072 + 0.000584 = 0.000656。
玩家 4 可以通过两种方式安全过关:
- 玩家 3 安全过关。在这种情况下,玩家 4 只需复制他的步骤即可。
- 在玩家 1 到 4 之间,只有 3 个坏步骤。从 18 对玻璃中选择 3 个来杀死玩家 1 到 3 的两块玻璃,一共有 combin(18,3)=816 种方法。15 个好步骤和 3 个坏步骤的概率是 816*(1/2)^2 = 816/262144 = 0.003113。
按照这个逻辑,我们得到以下每个球员的概率表。
桥牌
| 玩家 | 可能性 生存 |
|---|---|
| 1 | 0.000004 |
| 2 | 0.000072 |
| 3 | 0.000656 |
| 4 | 0.003769 |
| 5 | 0.015442 |
| 6 | 0.048126 |
| 7 | 0.118942 |
| 8 | 0.240341 |
| 9 | 0.407265 |
| 10 | 0.592735 |
| 11 | 0.759659 |
| 12 | 0.881058 |
| 十三 | 0.951874 |
| 14 | 0.984558 |
| 15 | 0.996231 |
| 16 | 0.999344 |
| 全部的 | 7.000076 |
以封闭形式表达答案,即:
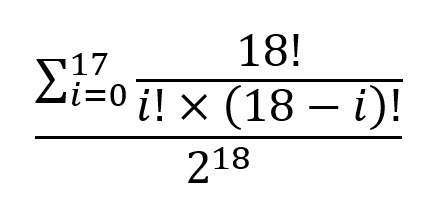
我在Wizard of Vegas论坛上提出并讨论了这个问题。
在你的终极 X 金牌中,3:10 时你拿到了一张四点同花顺,也就是三点和四点。你从 2 到 4 的任何四点同花的乘数是 9 倍。而葫芦的乘数是 1 倍。为什么你保留了四点同花顺,而不是只保留三张 3,而是尝试获得乘数更大的四点同花呢?
你说得对,我那只手确实搞砸了。
回想一下,我玩的是10人玩法。因此,我拿到葫芦的赢利是10×35 = 350。
如果只持有三,那么每手牌的概率如下:
- 四条 — 4.26%
- 满堂彩——6.11%
- 三条 — 89.64%
以下是乘数之后每手牌的赢利:
- 四条 — 1800
- 满堂彩——35
- 三条 — 15
如果只持有三条,我的预期收益将是 (4.26% * 1800) + (6.11% * 35) + (89.64% * 15) = 92.17854。这比葫芦的 35 倍要高得多。所以,没错,我在那手牌上犯了一个尴尬的错误。
有人向我挑战,要我进行以下赌注。我可以从一副标准扑克牌中选择任意三个点数,写下我的预测,但要保密到最后。例如,7-A-2。然后他提出和我打等额赌注,如果他猜对三次,他至少能猜出我的一个点数。我赢的几率是多少?
要想获胜,对手的三次预测都必须全部错误。第一次预测有 10/13 的概率是错误的。第二次预测有 9/12 的概率是错误的,因为我们可以排除第一个猜测的排名的可能性。第三次预测有 8/11 的概率是错误的,因为我们可以排除前两个猜测的排名的可能性。
这三件事必须同时发生,你才能获胜。因此,你获胜的概率是 (10/13) * (9/12) * (8/11) = 720/1716 = 41.96%。
在均等赌注下,从您的角度来看,这场赌注的庄家优势是 16.08%(哎哟!)。
这个问题摘自欧文·埃谢 (Owen E'Shea) 所著的《命题赌注之书》(第 7 期)。


