请问巫师 #352
密西西比扑克中最高赔付能增加多少赌场优势?
问得好。密西西比梭哈玩家肯定应该意识到,最高赔付可能会减少他们在同花大顺上的赢利,从而增加赌场优势。
密西西比扑克中,皇家同花顺的最高赔率是500比1,并且适用于所有投注。玩家有两次机会加注至底注的3倍,因此最终下注最高可达底注的7倍。如果玩家希望获得皇家同花顺,则应该尽可能加注。
在密西西比扑克中,玩家在底注(Ante)上的最大投注额应为最高赔付额/3500,且不受赔付上限的影响。例如,如果最高赔付额为80,000美元,那么我建议底注的最高投注额为22.86美元。我会将其四舍五入为20美元。
下表显示了不同投注额和常见最高赢额的赌场优势。该表假设玩家采用最佳策略,且赢额不设上限。请注意,随着投注额的增加和上限的降低,赌场优势会随之增加。
有赔付上限的庄家优势
| 赌注 | 5万美元上限 | 8万美元上限 | 10万美元上限 |
|---|---|---|---|
| 15美元 | 5.02% | 4.91% | 4.91% |
| 20美元 | 5.15% | 4.91% | 4.91% |
| 25美元 | 5.22% | 5.04% | 4.91% |
| 50美元 | 5.38% | 5.28% | 5.22% |
| 75美元 | 5.49% | 5.37% | 5.33% |
| 100美元 | 5.64% | 5.41% | 5.38% |
我在Wizard of Vegas论坛上提出并讨论了这个问题。
Vital Vegas 严厉批评了一位玩家,因为他在赢得 110 万美元的累积奖金后只给了 200 美元小费。在这种情况下,应该如何正确对待小费?
是的,虽然他们因为小费太少而责备玩家,但他们却巧妙地回避了小费应该是多少才合适的问题。
不仅大奖的小费礼仪没有明确的定义,就连小额奖金的小费礼仪也同样没有明确的定义。人们对此的看法五花八门,其中很多观点来自从未中过大奖的人。
首先,我要强调的是,小费并非可有可无。在赌场,根据赢的金额和服务水平,支付小费是理所当然的。这时,你很容易变成“粉红先生”,为自己不该给小费找借口。小费制度肯定存在缺陷,但这就是我们现有的制度。如果你不同意并拒绝给小费,那就不要要求任何需要小费的服务。
其次,一旦确定了玩家中奖,应该给多少小费?我这里讨论的只是玩家只中了一个大奖的情况。如果玩家中了很多大奖,规则会有所不同,这在高额投注时很正常。记住,审核大奖文件的规则如下:
- 在“老虎机”上赢得 1,200 美元或更多。
- 在基诺游戏中赢得 1,500 美元或更多。
- 在 AA 扑克锦标赛中赢得 5,000 美元或更多。
- 在桌面游戏中赢得 600 美元或更多,并且赌注至少为 300 倍。
我建议给多少小费?我以前说过奖金的0.5%到2%,奖金越高,给的百分比就越低。不过,当时我还没想过奖金会这么高。我觉得这个范围在10万美元左右比较合适。
这个问题促使我创建了一个具体的公式,我认为它适用于从1200美元到数百万美元的任何累积奖金。公式如下:
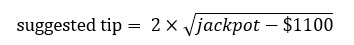
如果您看不到图像,它是 2×sqrt(jackpot-$1100)。
以下是一些常见累积奖金数额的计算公式。
建议小费表
| 大奖 | 提示 |
|---|---|
| 1,200美元 | 20美元 |
| 2,000 美元 | 60美元 |
| 5,000 美元 | 125美元 |
| 10,000美元 | 189美元 |
| 2万美元 | 275美元 |
| 5万美元 | 442美元 |
| 10万美元 | 629美元 |
| 100万美元 | 1,999美元 |
如果是110万美元,我的公式建议是2096.57美元。我认为四舍五入到2000美元就可以了。当然,也要考虑其他因素,比如服务质量。
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
对于任意给定的大数,该数附近的素数之间的平均距离是多少?此外,小于该数的素数有多少个?
对于任意大数 n 附近的素数之间的平均距离,一个非常好的估计方法是 ln(n)。这个估计器的精度令人惊叹。
作为佐证,下表列出了前 1500 万个素数的范围,以百万为一组。该表列出了素数之间范围内的平均距离以及平均距离的估计值。该估计值是该范围内最大和最小素数平均值的自然对数。例如,对于第 15 组一百万个素数,其值为 ln((256,203,221+275,604,541)/2)。
素数之间的平均距离
| 第一总理 在范围内 | 最后的素数 在范围内 | 素数 在范围内 | 平均距离 | 估计 | |
|---|---|---|---|---|---|
| 2 | 15,485,863 | 1,000,000 | 15.485861 | 15.86229105 | |
| 15,485,867 | 32,452,843 | 1,000,000 | 16.966976 | 16.9922867 | |
| 32,452,867 | 49,979,687 | 1,000,000 | 17.52682 | 17.53434381 | |
| 49,979,693 | 67,867,967 | 1,000,000 | 17.888274 | 17.89175615 | |
| 67,867,979 | 86,028,121 | 1,000,000 | 18.160142 | 18.15864108 | |
| 86,028,157 | 104,395,301 | 1,000,000 | 18.367144 | 18.3716137 | |
| 104,395,303 | 122,949,823 | 1,000,000 | 18.55452 | 18.54883262 | |
| 122,949,829 | 141,650,939 | 1,000,000 | 18.70111 | 18.70058553 | |
| 141,650,963 | 160,481,183 | 1,000,000 | 18.83022 | 18.83322787 | |
| 160,481,219 | 179,424,673 | 1,000,000 | 18.943454 | 18.95103217 | |
| 179,424,691 | 198,491,317 | 1,000,000 | 19.066626 | 19.05703535 | |
| 198,491,329 | 217,645,177 | 1,000,000 | 19.153848 | 19.15337672 | |
| 217,645,199 | 236,887,691 | 1,000,000 | 19.242492 | 19.24163365 | |
| 236,887,699 | 256,203,161 | 1,000,000 | 19.315462 | 19.32305683 | |
| 256,203,221 | 275,604,541 | 1,000,000 | 19.40132 | 19.39864545 |
资料来源:Prime Pages 上的Primes 之间的差距。
要计算任意给定数下的素数个数,我们可以先对 ln(n) 的平均距离估计值求积分。这样就能得到任意数 n 以内的素数之间平均距离的总和。
f(n)=ln(n) 的积分是多少?回想一下分部积分法告诉我们:
f(n)*g'(n) 的积分 dn = f(n)*g(n) - (f'(n)*g(n)) 的积分 dn
设 f(n)=ln(n) 且 g'(n)=1。则 f'(n)=1/n 且 g(n)=n。因此,ln(n) 的积分为 ln(n)*n - ((1/n)*n) 的积分 = ln(n)*n - n = n*(ln(n)-1)
如果我们将 n*(ln(n)-1) 除以 n,我们就能得到从 2 到 n 范围内素数之间的平均距离。这个距离就是 ln(n)-1。
如果我们将 n 除以素数之间的平均距离,我们会得到 n 以下素数的平均数量,等于 n/(ln(n)-1)。
作为证据,下表列出了各种大数下的素数个数及其估计值。Excel 只允许 15 位有效数字,请谅解。拜托,谁能制作一个能处理更多数字的电子表格吧。
素数之间的平均距离
| n | n 以下的素数 | n/(ln(n)-1) |
|---|---|---|
| 10 | 4 | 8 |
| 100 | 二十五 | 二十八 |
| 1,000 | 168 | 169 |
| 10,000 | 1,229 | 1,218 |
| 10万 | 9,592 | 9,512 |
| 1,000,000 | 78,498 | 78,030 |
| 10,000,000 | 664,579 | 661,459 |
| 1亿 | 5,761,455 | 5,740,304 |
| 1,000,000,000 | 50,847,534 | 50,701,542 |
| 10,000,000,000 | 455,052,511 | 454,011,971 |
| 100,000,000,000 | 4,118,054,813 | 4,110,416,301 |
| 1,000,000,000,000 | 37,607,912,018 | 37,550,193,650 |
| 10,000,000,000,000 | 346,065,536,839 | 345,618,860,221 |
| 100,000,000,000,000 | 3,204,941,750,802 | 3,201,414,635,781 |
| 1,000,000,000,000,000 | 29,844,570,422,669 | 29,816,233,849,001 |
| 10,000,000,000,000,000 | 279,238,341,033,925 | 279,007,258,230,820 |
| 100,000,000,000,000,000 | 2,623,557,157,654,230 | 2,621,647,966,812,030 |
| 1,000,000,000,000,000,000 | 24,739,954,287,740,800 | 24,723,998,785,920,000 |
| 10,000,000,000,000,000,000 | 234,057,667,276,344,000 | 233,922,961,602,470,000 |
| 100,000,000,000,000,000,000 | 2,220,819,602,560,910,000 | 2,219,671,974,013,730,000 |
| 1,000,000,000,000,000,000,000 | 21,127,269,486,018,700,000 | 21,117,412,262,910,000,000 |
| 10,000,000,000,000,000,000,000 | 201,467,286,689,315,000,000 | 201,381,995,844,660,000,000 |
| 100,000,000,000,000,000,000,000 | 1,925,320,391,606,800,000,000 | 1,924,577,459,166,810,000,000 |
| 1,000,000,000,000,000,000,000,000 | 18,435,599,767,349,200,000,000 | 18,429,088,896,563,900,000,000 |
| 10,000,000,000,000,000,000,000,000 | 176,846,309,399,143,000,000,000 | 176,788,931,049,964,000,000,000 |
来源:有多少个素数?在素数页面上。


