请问巫师 #341
要使两个骰子的总点数从 2 到 12 不等,预计需要掷多少次?请使用微积分来解答。
[剧透=解决方案]
回想一下,掷出总数为 2 的概率是 1/36。在 t 次掷骰中,预期掷出总数为 2 的次数为 t/36。假设掷骰间隔时间呈指数分布,平均值为 t/36。泊松分布告诉我们,掷出总数为 2 的次数为零的概率为 exp(-t/36)。
回想一下,掷出总数 3 的概率是 2/36 = 1/18。按照同样的逻辑,泊松分布告诉我们,掷出总数 3 且掷出次数为零的概率是 exp(-t/18)。
回想一下,掷出总数 4 的概率是 3/36 = 1/12。按照同样的逻辑,泊松分布告诉我们,掷出总数 4 且掷出次数为零的概率是 exp(-t/12)。
回想一下,掷出总数 5 的概率是 4/36 = 1/9。按照同样的逻辑,泊松分布告诉我们,掷出总数 5 且掷出次数为零的概率是 exp(-t/9)。
回想一下,掷出总点数 6 的概率是 5/36。按照同样的逻辑,泊松分布告诉我们,掷出总点数 6 且掷出零点的概率是 exp(-5t/36)。
回想一下,掷出总数 7 的概率是 6/36 = 1/6。按照同样的逻辑,泊松分布告诉我们,掷出总数 7 且掷出零次的概率是 exp(-t/6)。
8 到 12 的概率与 2 到 6 的概率相同。
因此,每个总数中的 t 个单位至少被滚动一次的概率是:
(1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
在 t 个时间单位内至少 total 未滚动的概率为 1 - (1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
为了得到没有至少一个总数的预期时间,我们将上述函数从 0 积分到无穷大。
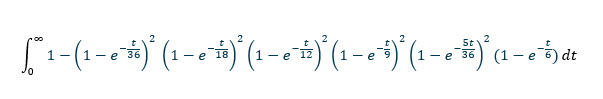
积分计算器(我推荐这个)可以轻松解决这个问题,因为 769767316159/12574325400 = apx。61.2173847639572 卷。
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
反复掷两个骰子,一个红色骰子,一个蓝色骰子。记录每个骰子的点数之和。当两个骰子点数相等时,预期角色数是多少?
[剧透=更多评论]
很难解释为什么答案是无穷大。更令人困惑和矛盾的是,总数相等的概率是1。
下表显示了 1 至 16 次投掷后总数首次相同的概率。
概率首次等于总数
| 面包卷 | 可能性 |
|---|---|
| 1 | 0.166667 |
| 2 | 0.112654 |
| 3 | 0.092850 |
| 4 | 0.080944 |
| 5 | 0.072693 |
| 6 | 0.066539 |
| 7 | 0.061722 |
| 8 | 0.057819 |
| 9 | 0.054573 |
| 10 | 0.051819 |
| 11 | 0.049443 |
| 12 | 0.047367 |
| 十三 | 0.045532 |
| 14 | 0.043895 |
| 15 | 0.042423 |
| 16 | 0.041089 |
Excel 显示与该曲线非常接近的拟合值为 y = 0.1784*x-1.011,其中 x = 滚动次数,y = 概率。
这个无穷级数的和是无穷大。
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
宾夕法尼亚现金5游戏的盈亏平衡头奖是多少?你可以忽略税费和头奖分成。
首先,我们来了解一下规则。投注额为2美元。游戏规则是,从43个球中抽出5个球。赔率表如下:
- 第 5 场比赛 = 大奖
- 数学 4 = 200 美元
- 第三场比赛 = 10 美元
- 第二场比赛 = 2 美元
此外,玩家还会得到一张刮刮卡,我猜是一张刮刮卡。这张卡有 1/80 的概率支付 6 美元,1/5 的概率支付 2 美元。
下表是我对基础游戏的分析。结果显示,中2到4个号码的价值为0.287784美元。
现金 5 返还表
| 抓住 | 支付 | 组合 | 可能性 | 返回 |
|---|---|---|---|---|
| 5 | 大奖 | 1 | 0.000001 | ? |
| 4 | 200 | 190 | 0.000197 | 0.039477 |
| 3 | 10 | 7030 | 0.007303 | 0.073032 |
| 2 | 2 | 84360 | 0.087638 | 0.175276 |
| 1 | 0 | 369075 | 0.383416 | 0.000000 |
| 0 | 0 | 501942 | 0.521445 | 0.000000 |
| 全部的 | 0 | 962598 | 1.000000 | 0.287784 |
下表展示了我对“快速现金”即时赢取功能的分析。右下角单元格显示的价值为 0.475 美元。
即时现金返还表
| 抓住 | 支付 | 可能性 | 返回 |
|---|---|---|---|
| 6 | 1 | 0.012500 | 0.075000 |
| 2 | 16 | 0.200000 | 0.400000 |
| 0 | 63 | 0.787500 | 0.000000 |
| 全部的 | 80 | 1.000000 | 0.475000 |
因此,非累积奖金的价值为 0.287784 美元 + 0.475000 美元 = 0.762784 美元。
设 j 等于盈亏平衡的累积奖金金额。则:
2 = 0.762784 + j × (1/962598)
1.237216 = j × (1/962598)
j = 1.237216 × 962598
j = 1,190,941.95 美元。
总回报率为 0.381392,加上每 100,000 美元大奖的 0.051943。
正如问题中所述,所有这些都忽略了税收和奖金分享。
我在Wizard of Vegas论坛上提出并讨论了这个问题。


