请问巫师 #338
使用两个骰子,要获得从 2 到 12 的总数,平均需要掷多少次?
[剧透=解决方案]
这个问题可以用马尔可夫链来回答,但我更喜欢用微积分。关键在于,如果投掷间隔时间服从均值为1的指数分布,答案是一样的。也就是说,答案可以表示为从0到无穷大的积分:
1-(1-exp(-x/36))^2*(1-exp(-x/18))^2*(1-exp(-x/12))^2*(1-exp(-x/9))^2*(1-exp(-5*x/36))^2*(1-exp(-x/6))
您可以使用积分计算器轻松解决此类积分。
您也可以使用我的预期试验次数计算器来解决任何此类问题。
[/spoiler]正方形中间有一只蚂蚁,它距离左上角17英寸,距离右上角20英寸,距离右下角13英寸。
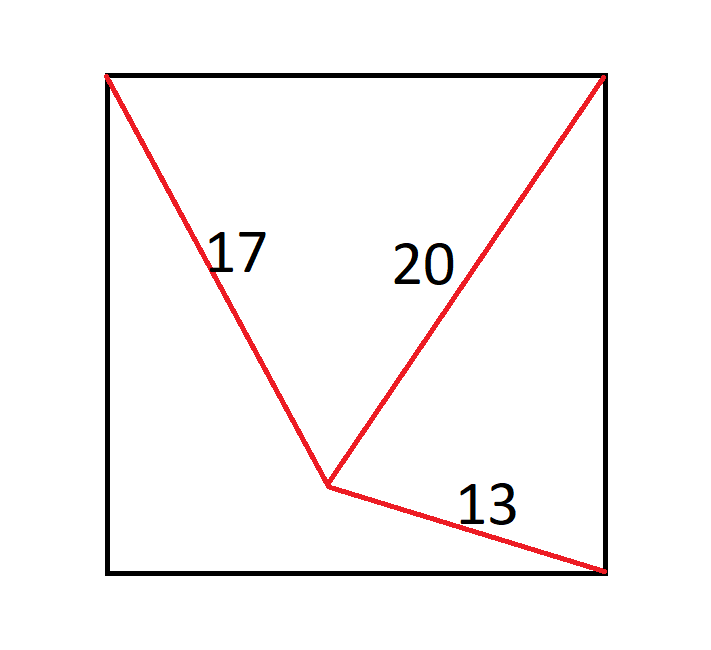
这个正方形有多大?
[剧透=有用的公式] c^2 = a^2 + b^2 -2ab*cos(c)
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)
[剧透=解决方案]
首先,将三角形ABE旋转90度,形成一个新的三角形BDF。
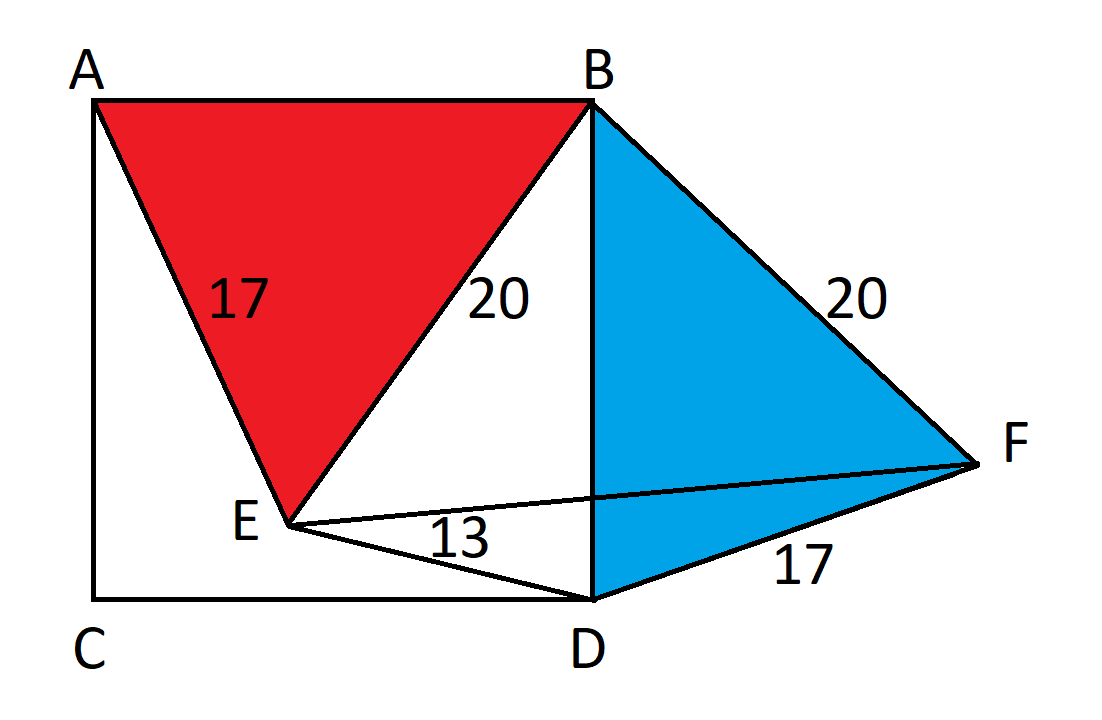
由于三角形旋转了90度,根据定义,角EBF=90。根据勾股定理,EF = 20*sqrt(2)。
根据余弦定律:17^2 = 13^2 + (20*sqrt(2))^2 - 2*13*20*sqrt(2)*cos(DEF)。
289 = 169 + 800 - 520*sqrt(2)*cos(DEF)
520*sqrt(2)*cos(DEF) = 680。
cos(DEF) = 17*sqrt(2)/26。
回想一下,sin^2(x) + cos^2(x) = 1。让我们用它来求解 sin(DEF)。
sin^2(DEF) + cos^2(DEF) = 1
sin^2(DEF) + (17*sqrt(2)/26)^2 = 1
sin^2(DEF) + 289/338 = 1
sin^2(DEF) = 49/338
sin(DEF) = 7*sqrt(2)/26
接下来,考虑角度 BED。
角度 BED = 角度 BEF + 角度 FED。
我们知道 EBF 是 90 度,并且是一个等腰三角形。这样一来,角 BEF 就是 45 度。
因此,角度 BED = 45 度 + 角度 FED。
回想一下,cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)。
cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - sin(BEF)*sin(FED)
= (1/sqrt(2))*17*sqrt(2)/26 - (1/sqrt(2))*7*sqrt(2)/26
= (17/26) - (7/26) = 10/26 = 5/13
让我们再次应用余弦定律,这次针对三角形 BED。
BD^2 = 20^2 + 13^2 - 2*20*13*(5/13)
= 400 + 169 - 200 = 369
BD 是所讨论正方形的边长,因此 BD^2 是该正方形的面积,我们已经表明其面积为 369。
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
投掷死亡游戏 (Drop Dead) 使用五个标准骰子进行。回合开始时,您需掷出所有五个骰子。如果所有骰子都不是 2 或 5,则计算所有骰子点数之和,并将结果添加到您的点数中,然后重新掷骰。如果掷出任何 2 或 5,则您的本轮得分为零。所有显示 2 或 5 的骰子均视为死局,并作废。然后,您使用剩余的骰子重新掷骰。游戏继续,您可以选择得分或移除骰子。当所有骰子都被移除后,您的回合结束,即您被判定为投掷死亡。所有得分将加在一起,得出您的最终得分。得分高者获胜。
您对这场比赛的预期得分是多少?
[剧透=解决方案]
让我们从剩下一个骰子的场景开始并向后移动。
设变量 a 为剩余一个骰子时的预期附加点数。
除 2 或 5 之外的平均掷点数为 (1+3+4+6)/4 = 7/2。
a = (2/3)×(a + 7/2)。
a/3 = 7/3。
a = 7。
接下来我们计算一下剩下两个骰子的预期点数b。
b = (2/3) 2 ×(b + 2 × (7/2)) + 2×(2/3)×(1/3)×a。
b = 11.2。
接下来我们计算一下剩下三个骰子的预期点数c。
c = (2/3) 3 ×(c + 3× (7/2)) + 3×(2/3) 2 ×(1/3)×b + 3×(2/3)×(1/3) 2 ×b。
c = 1302/95 = 13.705263。
接下来,我们来计算剩下四个骰子的预期点数d。
d = (2/3) 4 ×(d + 4× (7/2)) + 4×(2/3) 3 ×(1/3)×c + 6×(2/3) 2 ×(1/3) 2 ×b + 4×(2/3)×(1/3) 3 ×a。
d = 3752/247 = 15.190283。
最后,我们来计算一下剩下五个骰子的预期点数e。
e = (2/3) 5 ×(e + 5×(7/2)) + 5×(2/3) 4 ×(1/3)×d + 10×(2/3) 3 ×(1/3) 2 ×c + 10×(2/3) 2 ×(1/3) 3 ×b + 5×(2/3)×(1/3) 4 ×a。
e = 16.064662。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
以三张牌扑克中的对子加注为例,它遵循1-4-6-30-40的赔率表。然而,黑桃小皇家牌的赔率是累积奖金,其他三种花色的小皇家牌的赔率是累积奖金的25%。为了公平起见,计量表需要多高?


