请问巫师 #323
这张联赢卡好用吗?

第一步,你必须在NFL比赛中押注让分盘。你提问时(2020年1月2日),维京人队领先7.5分。根据我的NFL替代让分计算器,维京人队+8.5获胜的概率为52.22%。
对于所有其他游戏,我查看了当前的胜负盘口,减去抽水,得出了获胜概率。下表显示了每局的获胜概率。
威廉希尔过关卡
| 腿 | 美酒 | 概率获胜 |
|---|---|---|
| 圣徒队 -8.5 | -7.5 | 47.78% |
| 维京人 +8.5 | 8.5 | 52.22% |
| 侯 | -135 | 57.45% |
| 账单 | 135 | 42.55% |
| 爱国者队 | -205 | 67.21% |
| 泰坦 | 205 | 32.79% |
| 海 | -118 | 54.13% |
| 菲尔 | 118 | 45.87% |
| 路易斯安那州立大学 | -200 | 66.67% |
| 克莱姆森 | 200 | 33.33% |
| 亚足联 | -130 | 56.52% |
| 近场通信 | 130 | 43.48% |
第一步中,最有可能获胜的两个球队是爱国者队和路易斯安那州立大学队。以下是我推荐的球队获胜的概率:
- 维京人队 +8.5 — 52.22%
- 爱国者——67.21%
- 路易斯安那州立大学——66.67%
这些概率的乘积是23.40%。如果1赔4,回报率为4 × 23.40% = 93.60%。换句话说,赌场优势是6.40%。所以,我不考虑这个。
我正在考虑为“push 22”二十一点变体创建一个边注,如果庄家以 22 点爆牌,则赔率为 11 比 1。赔率是多少?
我正在考虑为“push 22”二十一点变体创建一个边注,如果庄家爆牌 22,那么我就能赢。赔率是多少?赌场优势是多少?
假设庄家总是抽出他的牌(即使每个玩家都已经爆牌),那么如果庄家在软 17 点停牌,那么在 22 点爆牌的概率为 7.88%,如果他拿到软 17 点,那么在 22 点爆牌的概率为 8.00%。
假设庄家拿到软17点,赔率为11比1时,赌场优势为4.04%。赔率为10比1时,赌场优势将跃升至12.04%。
我应该警告你并建议玩家这是可数的(闭嘴,Wiz!)。
艾米和鲍勃举办了一场比赛,看谁能率先赢得四次抛硬币的胜利。艾米想押 8,000 美元赌自己获胜。但是,她一次只能押一次硬币。所有赌注的赔率相同。她该如何安排赌注,才能确保如果她赢了四次,她就能赢得 8,000 美元;如果鲍勃赢了,她就能输掉 8,000 美元?
点击下面的按钮获取答案。
系列中期共有16种可能的状态。下表显示了Amy在每种情况下应该下的注额,以及她按照此策略下注前的余额。
回答
| 艾米 | 鲍勃 | 平衡 | 赌注 |
|---|---|---|---|
| 0 | 0 | 0 | 2500 |
| 0 | 1 | -2500 | 2500 |
| 0 | 2 | -5000 | 2000 |
| 0 | 3 | -7000 | 1000 |
| 1 | 0 | 2500 | 2500 |
| 1 | 1 | 0 | 3000 |
| 1 | 2 | -3000 | 3000 |
| 1 | 3 | -6000 | 2000 |
| 2 | 0 | 5000 | 2000 |
| 2 | 1 | 3000 | 3000 |
| 2 | 2 | 0 | 4000 |
| 2 | 3 | -4000 | 4000 |
| 3 | 0 | 7000 | 1000 |
| 3 | 1 | 6000 | 2000 |
| 3 | 2 | 4000 | 4000 |
| 3 | 3 | 0 | 8000 |
单击下面的按钮获取解决方案。
[剧透=解决方案]让:
- a = 艾米获胜
- b = Bob 获胜
- w = 艾米迄今为止在系列赛中的净胜场
- f(a,b,w) = Amy 下一场比赛的下注额
在这类谜题中,通常好的策略是从头到尾,然后一路回到开头。话虽如此,很容易看出:
f(3,3,0) = 8,000
在这种情况下,第七局是“赢家通吃”。艾米应该赢得 0,并在最后一轮下注 8,000,如果她赢了,她将赢得 8,000,否则将损失 8,000。
退一步说,如果她赢了3次,鲍勃赢了2次,结果会怎样?如果她赢了下一轮,她就赢了整局。如果她输了,比分将是3-3。根据f(3,3,0),如果比分是3,3,她应该得0。所以,如果她赢了下一轮,我们需要她有8,000,否则得0。这样一来,她净赢了4,000,下注金额也相同。所以:
f(3,2,4000)=4,000
再回过头来看,如果她赢了3局,而鲍勃赢了1局,结果会怎样?如果她下一轮赢了,她就赢了整局。如果她输了,比分将是3-2。根据f(3,2,4000),如果比分是3,2,她应该有4,000。所以,如果她下一轮赢了,我们需要她有8,000,否则她有4,000。这样一来,中间的净赢利是[(4,000+8,000)/2=6,000],下注金额是这两个目标之间距离的一半,即[(8000-4000)/2 = 2000]。所以:
f(3,1,6000) = 2,000
再退一步,假设她赢了3次,而鲍勃没有赢,结果会怎样?如果她赢了下一轮,她就赢了整场比赛。如果她输了,比分将是3-1。根据f(3,1,6000),如果比分是3,1,她应该有6,000。所以,如果她赢了下一轮,我们需要她有8,000,否则有6,000。这样一来,中间的净赢利是[(6,000+8,000)/2=7,000],下注金额是这两个目标之间距离的一半,即[(8000-4000)/2 = 2000]。所以:
f(3,0,7000) = 1,000
显而易见,如果比分打平,艾米的净赢额应该为0。在任何平局情况下,她赢得整个系列赛的概率都是50%。由于双方的胜负平衡目标均为8,000,她需要押注0,否则她将有可能无法达成任何最终目标。
接下来,如果艾米在系列赛中落后,她的净赢额应该是她领先相同分数时净赢额的-1倍。例如,假设艾米的比分是2比3(或2比3)。如果她下一轮输了,她就输掉了整场比赛。如果她赢了,她的比分将是3比3。根据f(3,3,0),如果比分是3比3,她应该得0。所以,我们需要她赢下一轮时得0,否则得-8000。这样一来,她的净亏损就介于4000和相同金额的下注之间。所以:
f(2,3,-4000)=4,000
按照同样的逻辑:
f(1,3,-6000) = 2,000
f(0,3,-7000) = 1,000
接下来,如果比分是 2-2,艾米应该下注多少?如果她赢了,比分将是 3-2。从上文可以看出,她需要在这个比分下净赢 4,000。如果她以 2-3 落后,我们需要她净输 4,000。因此,她需要下注 4,000:
f(2,2,0) = 4,000
再退一步来看,如果比分是 2-1 会怎样?我们已经确定,如果她下次掷骰子赢了(比分 3-1),她需要净赢 6,000,如果她输了(比分 2-2),她需要净赢 0。这样一来,她会得到中间值 [(6,000+0)/2=3,000] 的净赢,以及两个进球之间距离的一半的赌注 [(6,000-0)/2 = 3,000]。所以:
f(2,1,3000) = 3000
再回过头来看,如果她赢了两局,而鲍勃赢了零局,结果会怎样?如果她下次掷骰子赢了,比分将是3-0。如果她输了,比分将是2-1。如果比分是3-0,她应该净赢7000,如果比分是2-1,她应该净赢3000。如果比分是2-0,她应该净赢中间值[(7000+3000)/2=5000],并且下注金额是这两个进球之间距离的一半[(7000-3000)/2=2000]。所以:
f(2,0,5000) = 2000
通过翻转 Alice 两次获胜而 Bob 获胜次数较少的分数,我们还知道:
f(1,2,-3000) = 3000
f(0,2,-5000) = 2000
如前所述,如果系列赛双方势均力敌,艾米的净赢应为0,因此,当比分是1-1时,她的净赢应为0。当比分是2-1时,她需要赢2,000;当比分是1-2时,她需要输2,000。因此,当比分是1-1平局时,她应该下注2,000,或者:
f(1,1,0) = 2,000
如果艾米1-0领先怎么办?我们已经确定,她需要在2-0时领先5,000。在1-1时,她需要持平。如果比分是 1-0,那么净胜球数为中间值 [(5,000+0)/2=2,500],投注额为两个进球距离的一半 [(5000-0)/2 = 2,500]。因此:
f(1,0,2500) = 2,500
将比分扳为 0-1:
f(0,1,-2500) = 2,500
所以,最终,我们在第一局比赛中比分为 0-0。我们需要艾米在下一轮赢的情况下赢 2,500,输的情况下输 2,500。因此,下注 2,500 就能达到这个目标。或者:
f(0,0,0) = 2,500
[/spoiler]这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
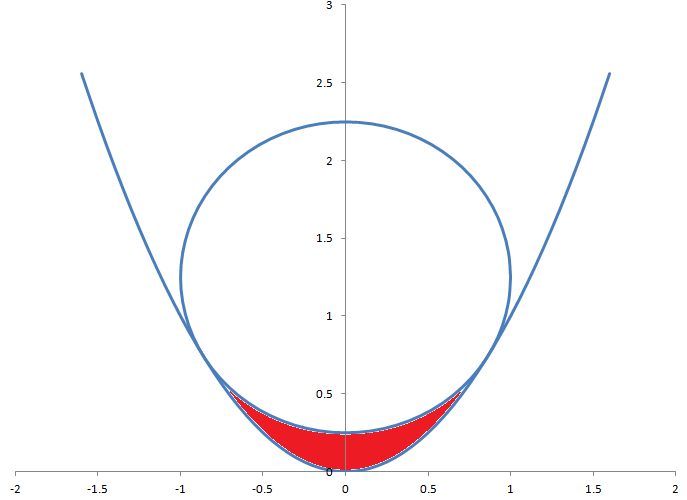
半径为 1 的圆与方程 y=x 2的抛物线相切。圆与抛物线之间的红色区域面积是多少?
点击下面的按钮获取答案。
这是我的解决方案。(PDF)
我在Wizard of Vegas论坛上提出并讨论了这个问题。
我从Mind Your Decisions的 Presh Talwalker 那里遇到了这个问题。


