WOO logo

Wizard 巫师推荐

请问巫师 #307

我正在参加2018年的“死亡池”活动。规则如下：

  1. 每位参赛者必须提交一份十位 100 岁以下在世名人的名单。
  2. 如果任何名人在 2018 年去世（美联社提到有证据证明），那么名单上有该名人名字的任何人都将获得 100-x 分，其中 x 是去世时的年龄。
  3. 2019 年 1 月 1 日得分最高的玩家获胜。

从平均值来看，这个游戏的最佳策略是什么？

anonymous

作为一名前精算师，你问对人了。希望精算师协会不会认为我的回答是对职业的滥用。话虽如此，为了回答你的问题，我查阅了我之前工作单位——社会保障局首席精算师办公室——的2014年期间寿命表。

周期生命表显示了 2014 年任何特定年龄和性别的人的死亡概率等。利用这些信息，我创建了下表，其中显示了从 0 到 100 岁的所有年龄段和两种性别的死亡概率和预期分数。

2014年期间生命表死亡池

年龄概率
死亡——男性		概率
死亡——女性		预期的
积分 — 男性		预期的
积分 — 女性
0 0.006320 0.005310 0.632000 0.531000
1 0.000403 0.000352 0.039852 0.034835
2 0.000282 0.000221 0.027626 0.021683
3 0.000211 0.000161 0.020514 0.015612
4 0.000181 0.000131 0.017405 0.012556
5 0.000161 0.000111 0.015313 0.010515
6 0.000141 0.000111 0.013260 0.010405
7 0.000131 0.000101 0.012184 0.009360
8 0.000121 0.000091 0.011127 0.008334
9 0.000091 0.000081 0.008256 0.007328
10 0.000101 0.000091 0.009073 0.008154
11 0.000101 0.000081 0.008973 0.007168
12 0.000131 0.000101 0.011535 0.008861
十三0.000202 0.000131 0.017547 0.011389
14 0.000303 0.000151 0.026023 0.012992
15 0.000404 0.000191 0.034304 0.016267
16 0.000505 0.000232 0.042393 0.019464
17 0.000616 0.000272 0.051129 0.022582
18 0.000748 0.000302 0.061316 0.024796
19 0.000880 0.000343 0.071262 0.027768
20 0.001022 0.000373 0.081780 0.029855
21 0.001145 0.000404 0.090445 0.031884
22 0.001258 0.000444 0.098105 0.034643
23 0.001310 0.000475 0.100880 0.036546
24 0.001332 0.000495 0.101246 0.037625
二十五0.001344 0.000526 0.100811 0.039422
二十六0.001377 0.000556 0.101864 0.041162
二十七0.001389 0.000577 0.101371 0.042106
二十八0.001421 0.000608 0.102330 0.043740
二十九0.001454 0.000648 0.103234 0.046036
三十0.001507 0.000669 0.105517 0.046837
31 0.001530 0.000710 0.105584 0.048998
三十二0.001574 0.000751 0.107011 0.051084
33 0.001617 0.000813 0.108364 0.054454
三十四0.001661 0.000864 0.109644 0.057041
三十五0.001716 0.000926 0.111521 0.060194
三十六0.001781 0.001008 0.113970 0.064538
三十七0.001857 0.001081 0.116963 0.068090
三十八0.001933 0.001164 0.119830 0.072145
三十九0.002020 0.001237 0.123207 0.075427
40 0.002118 0.001340 0.127066 0.080422
41 0.002258 0.001445 0.133232 0.085232
四十二0.002410 0.001560 0.139778 0.090455
43 0.002615 0.001696 0.149075 0.096649
四十四0.002843 0.001853 0.159228 0.103761
45 0.003105 0.002011 0.170771 0.110606
46 0.003401 0.002191 0.183635 0.118300
四十七0.003742 0.002403 0.198314 0.127342
四十八0.004108 0.002647 0.213613 0.137656
49 0.004532 0.002894 0.231133 0.147577
50 0.004994 0.003194 0.249696 0.159718
51 0.005473 0.003487 0.268191 0.170880
52 0.005993 0.003794 0.287656 0.182103
53 0.006565 0.004104 0.308561 0.192871
54 0.007159 0.004428 0.329324 0.203676
55 0.007799 0.004767 0.350946 0.214498
56 0.008475 0.005153 0.372902 0.226729
57 0.009179 0.005534 0.394696 0.237972
58 0.009856 0.005889 0.413944 0.247347
59 0.010575 0.006272 0.433558 0.257150
60 0.011350 0.006683 0.453991 0.267338
61 0.012209 0.007180 0.476135 0.280016
62 0.013061 0.007720 0.496330 0.293355
63 0.013921 0.008339 0.515084 0.308537
64 0.014814 0.009029 0.533320 0.325041
65 0.015831 0.009839 0.554094 0.344371
66 0.016981 0.010741 0.577354 0.365197
67 0.018300 0.011752 0.603909 0.387812
68 0.019778 0.012879 0.632894 0.412117
69 0.021443 0.014142 0.664734 0.438397
70 0.023384 0.015613 0.701513 0.468376
71 0.025547 0.017271 0.740873 0.500852
72 0.027877 0.019047 0.780560 0.533320
73 0.030384 0.020918 0.820374 0.564797
74 0.033098 0.022938 0.860535 0.596385
75 0.036256 0.025299 0.906400 0.632465
76 0.039868 0.028043 0.956841 0.673035
77 0.043883 0.031127 1.009299 0.715914
78 0.048257 0.034590 1.061657 0.760984
79 0.053128 0.038456 1.115692 0.807583
80 0.058709 0.043007 1.174177 0.860145
81 0.065070 0.048186 1.236322 0.915536
82 0.072149 0.053762 1.298691 0.967712
83 0.079906 0.059769 1.358409 1.016065
84 0.088524 0.066380 1.416378 1.062085
85 0.098157 0.073823 1.472348 1.107351
86 0.108904 0.082381 1.524651 1.153334
87 0.120889 0.092180 1.571556 1.198344
88 0.134134 0.103305 1.609607 1.239664
89 0.148707 0.115744 1.635778 1.273180
90 0.164522 0.129477 1.645220 1.294772
91 0.181584 0.144435 1.634254 1.299911
92 0.199903 0.160621 1.599225 1.284970
93 0.219362 0.177816 1.535534 1.244713
94 0.239881 0.196194 1.439286 1.177165
95 0.260293 0.214694 1.301463 1.073469
96 0.280129 0.233056 1.120515 0.932225
97 0.299042 0.251152 0.897125 0.753456
98 0.316317 0.268235 0.632634 0.536471
99 0.332667 0.284442 0.332667 0.284442
100 0.348651 0.301417 0.000000 0.000000

该表显示，90 岁男性的最高预期分数为 1.645220。

这个问题是在我的非赌博论坛“Diversity Tomorrow”中提出和讨论的。

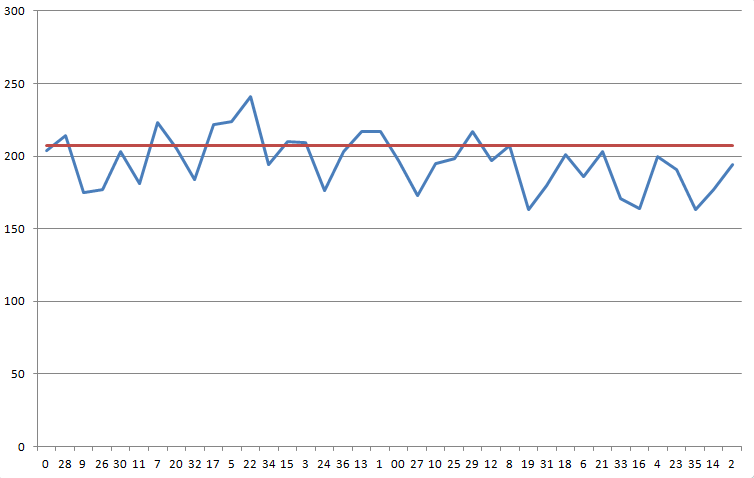
我记录了7456次轮盘赌的旋转。结果如下。我怀疑轮盘有偏差，但不确定数据是否足够确凿，可以玩这个游戏。

轮盘数据

获胜
数字		发生
0 204
二十八214
9 175
二十六177
三十203
11 181
7 223
20 205
三十二184
17 222
5 224
22 241
三十四194
15 210
3 209
24 176
三十六203
十三217
1 217
00 197
二十七173
10 195
二十五198
二十九217
12 197
8 207
19 163
31 180
18 201
6 186
21 203
33 171
16 164
4 200
23 191
三十五163
14 177
2 194
全部的7456

Bnitty

下图按顺序显示了您在轮盘上的结果。蓝线表示您的结果。红线表示您需要的数字 207.11，以克服 5.26% 的赌场优势。

对该分布进行卡方检验，结果显示自由度为 37，统计量为 68.1。出现这种或以上偏态分布的概率为 1/725。

我认为卡方检验并非适用于这种情况的最佳方法，因为它没有考虑结果的顺序，但我也不知道有更好的检验方法。有人建议使用Kolmogorov-Smirnov 检验，但我认为这并不合适。如果有其他合适的检验方法，我洗耳恭听。

我可以说，如果你押注围绕数字5的3个数字弧，那么你记录的旋转次数将获得10.57%的利润。然而，如果你押注围绕数字5的7个数字弧，利润率就会下降到2.84%。

如果非要用通俗易懂的语言来回答，我会说轮盘确实存在偏见，但并非确凿无疑的证据。然而，这种偏见可能不足以显著且自信地克服赌场优势。假设赌场不在赌桌之间调换轮盘，我认为在下大注之前应该收集更多数据。很抱歉，我的回答如此模棱两可。

这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。

两位玩家，山姆和丹，各有五枚硬币。两人都必须选择将一到五枚硬币放在手中。同时，两人必须透露所掷硬币的数量。如果两人选择的硬币数量相同，则山姆获胜并收集所有掷出的硬币。如果两人选择的硬币数量不同，则丹将收集所有掷出的硬币。假设两位玩家都是完美的逻辑学家，那么丹的最佳策略是什么？

ThatDonGuy

丹应该按如下方式随机化他的策略：

  • 挑选一枚硬币的概率 = 77/548。
  • 挑选一枚硬币的概率 = 107/548。
  • 挑选一枚硬币的概率 = 117/548。
  • 挑选一枚硬币的概率 = 122/548。
  • 挑选一枚硬币的概率 = 125/548。

采用这种策略，无论 Sam 挑选多少硬币，Dan 都有望每回合赢得 3.640510949 个硬币。

可以在我的数学问题网站问题 230 中找到解决方案。

在我的“拉斯维加斯巫师”论坛中可以找到与此相关的问题。

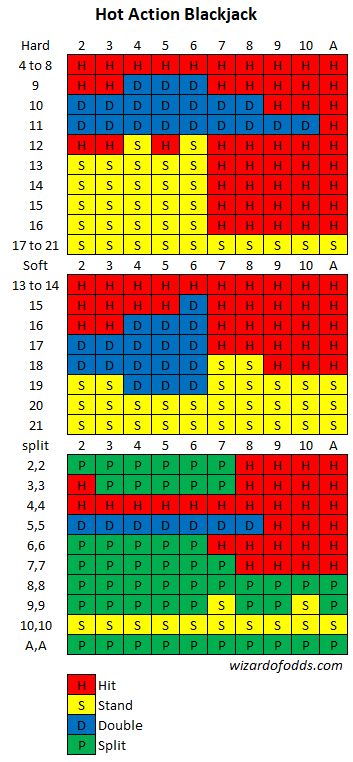
旧金山加州大赌场（California Grand Casino）正在推出一款名为“Hot Action Blackjack”的二十一点游戏。游戏规则如下：

  • 连续洗牌机中有六副牌，另外还有 18 张鬼牌，面值为 2。
  • 庄家拿到软 17。
  • 前两张牌加倍。
  • 重新分成四手。
  • 禁止抽牌或重新分割 A 牌。
  • 不投降。
  • 二十一点的赔率为 6 比 5。
  • 如果玩家的前两张牌是百搭牌，那么他将获得 4 比 1 的奖金。
  • 如果玩家的前两张牌是同花色的 A，那么他将获得 5 比 1 的奖金。
  • 玩家必须支付 5% 的佣金才能玩。

基本策略和庄家优势是什么？

JPClav

首先，这是我根据这些规则制定的基本策略：

综合考虑，我根据初始投注给出的赌场优势是 6.01%（哎哟！）。换句话说，如果玩家下注 100 美元（不计 5 美元佣金），那么他预计会损失 6.01 美元。这也解释了为什么在加州我建议远离玩家坐庄的游戏，除非你坐庄。

这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。