请问巫师 #270
我在一家允许无限次分牌的赌场玩。这条规则有什么作用?
我指出,与最多分牌至四手牌相比,无限次重新分牌的价值,如果该规则适用于所有对子(包括A),则价值为0.05%;如果不包含A,则价值为0.02%。这个问题是在我的配套网站“拉斯维加斯巫师”(Wizard of Vegas)的论坛上提出并讨论的。
显然,LVH 已经开出了一张 10 美元的弗吉尼亚联邦大学夺冠赔率 5000:1 的全国冠军票。如果弗吉尼亚联邦大学夺冠,那将支付 5 万美元。*如果*你持有这张票,你目前愿意接受的最低交易价格是多少?(最后 4 场明天开始)
我看到Pinnacle网站上弗吉尼亚联邦大学夺冠的赔率是:是+604,否-750。让我们算一下,你需要押注弗吉尼亚联邦大学不赢,才能锁定相同的赔率,以及最终的赔率是多少。设x为投注金额。胜率 = 50,000 - x
输的结果 = x*(100/750) = (2/15)x 设这些数相等 50000-x = (2/15)x 50000 = (17/15)xx = 50000×(15/17) x = $44,117.65 看看这样对不对……如果弗吉尼亚联邦大学赢了,结果是 $50,000 减去希尔顿的赔付,再减去 $44,117.65 给 Pinnacle,结果就是 $5,882.35 如果弗吉尼亚联邦大学输了,希尔顿什么也得不到,但是 Pinnacle 的赔率是 $44,117.65 × (100/750) = $5,882.35。不过,我怀疑押注弗吉尼亚联邦大学输球的赔率是否公平。如果老板极度厌恶风险,并且急于出售彩票,那么我认为 $6,000 左右比较公平。不过,我会根据弗吉尼亚联邦大学获胜的赔率+604来计算他们的获胜概率,这意味着获胜概率为100/704 = 14.2%。这样一来,这张彩票的价值就约为7100美元。这还不包括税收影响。这个问题是在我的配套网站 “拉斯维加斯巫师”(Wizard of Vegas)的论坛上提出并讨论的。
当不进行庄家游戏时,您在牌九扑克中能拿到的最好牌是什么?
不庄的时候,似乎没有什么牌是不可战胜的。所以,我们来考虑两手牌。第一手牌在高牌中既不能被击败,也不能被打平。第二手牌在低牌中既不能被击败,也不能被打平。
(1)AAAAW/KK(W=百搭)
五张 A 在高牌中无人能敌,但一对 K 在低牌中却可能打成平手。两张 K 的组合数为combin (44,5) = 1,086,008。剩余 46 张牌中,7 张牌的组合数总计为 53,524,680。因此,两张 K 的概率为 1,086,008/53,524,680 = 2.03%。由于这些组合很多,庄家不会在低牌中打出 KK。根据我的牌九扑克附录 1 ,庄家在高牌中拿到一对 A 或更小的牌的概率为 74.93%。这意味着他会组成两对或更好的牌,这让他有 25.07% 的概率在低牌中打出 K。因此,玩家获得两张 K 并能够将其打出低牌的概率为 2.03% × 25.07% = 0.51%,即 196 分之一。
(2)AWQJT(同花)/AA
皇家牌可以与高牌打平,但 A 不能与低牌打平。这里我用百搭牌代替 K 组成皇家牌,但它也可以代替 Q、J 或 T。我不想用它代替 A,因为那样一来牌堆里就剩下两张 A 让庄家打平低牌了。这样,庄家就只能用另一张皇家牌来与高牌打平。这种情况的几率是多少?皇家牌剩下三种花色,另外两张牌可以是任何花色。所以平局的组合数是 3×combin(41,2) = 2,460。玩家从原来的 43 张牌中拿走 7 张后,我从剩下的 46 张牌中得到 41 张,然后再减去庄家皇家牌中的 5 张牌中的 5 张。分母为 combin(46,7) = 53,524,680。因此,与 Wild Royal/AA 打平的概率为 2,460/53,524,680 = 0.004596%,即 21,758 分之一。
在某个完美主义者给我写信之前,我可能会遇到一些奇怪的情况,比如荷官没有按照我的意图出牌。我的目的并非求出每种情况的确切概率,而是想证明为什么我认为狂野皇家/AA 是牌九扑克中不庄牌时能拿到的最佳牌型。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
除了同卵双胞胎之外,我与同胞兄弟姐妹的基因有多少比例是相同的?
1/2。
如果我们用基诺彩票来类比,每个人都有40个基因,每个基因都代表一个基诺球。然而,每个球都有唯一的编号。当两个没有血缘关系的人交配时,就像把他们两人的80个球组合成一个漏斗,然后随机选择40个基因作为交配后代的基因。
所以,当你受孕时,你得到了一半的彩球,另一半则被浪费了。当你的兄弟姐妹受孕时,他/她得到了你出生时抽取的彩球的一半,以及另一半未被抽取的彩球。所以,你们的基因有50%是相同的。这和基诺彩票如果抽取40个号码,连续两次抽取平均会有20个相同的彩球的原因是一样的。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
一家生产桌椅的工厂配备了10台锯、6台车床和18台砂光机。制作一把椅子需要锯10分钟、车床5分钟和砂光5分钟才能完成。制作一张桌子需要锯5分钟、车床5分钟和砂光20分钟才能完成。一把椅子售价10美元,一张桌子售价20美元。工厂每小时应生产多少张桌椅才能获得最高收益?收益是多少?
设c代表每小时制作的椅子数量,t代表桌子数量。每小时收入为10×c + 20×t。
10把锯子每小时锯600分钟。已知一把椅子锯10分钟,一张桌子锯5分钟。因此,每小时产量限制为:
(1)10c + 5t <= 600
6台车床每小时加工时间共计360分钟。我们已知,锯一把椅子需要5分钟,锯一张桌子需要5分钟。因此,每小时产量限制为:
(2)5c + 5t <= 360
18台砂光机每小时可进行1080分钟的砂光作业。我们假设一把椅子需要锯5分钟,一张桌子需要锯20分钟。因此,每小时的产量限制为:
(3)5c + 20t <= 1080
下图显示了三组机器所施加的三个约束。工厂可以生产符合所有三条线的任意椅子和桌子组合。问题是,在三条线下,哪个组合能带来最大的收益。
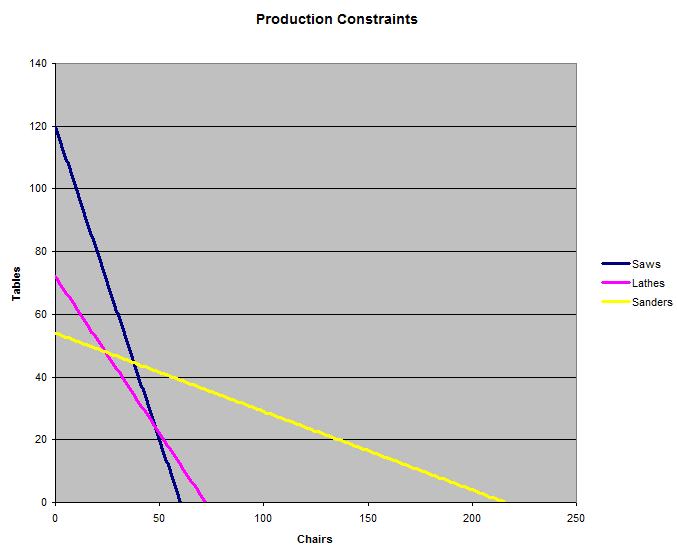
按理说,答案应该是两条线的交点、所有椅子或所有桌子。那么,让我们找出这两条线的交点。首先,让我们找出公式 (1) 和公式 (2) 的交点。我们可以将 <= 表达式改为 =,以最大限度地发挥机器的潜力。
(1)10美分+5吨=600
(2)5c + 5t = 360
从 (1) 中减去 (2):
5美分=240
c = 48
将 48 代入公式 (1) 中,得到 c:
10×48 + 5t = 600
5t = 120
t = 24
因此,等式 (1) 和 (2) 在 48 把椅子和 24 张桌子处相交。
接下来,让我们找出方程 (2) 和 (3) 的交点:
(2)5c + 5t = 360
(3)5c + 20t = 1080
从 (3) 中减去 (2):
15吨=720
t = 48
将其代入 (2) 或 (3) 中,我们可以解出 c,即 24。
因此,等式 (2) 和 (3) 在 24 把椅子和 48 张桌子处相交。
我们不需要费心寻找方程 (1) 和 (3) 的交点,因为我们可以从图中看到锯线和砂光机线的交点在车床约束之外。
也可能只做椅子才是正确答案。图表显示,锯子是只做椅子的最大限制因素。根据公式 (1),如果我们将桌子数量代入 0,则 c=60。
另一种可能性是只做桌子。图表显示,砂磨机将是最大的限制因素。将0把椅子代入公式(3),我们发现最多只能做54张桌子。
下图显示了每个可行答案的总收入。记住,每把椅子的收入是10美元,每张桌子的收入是20美元。
每小时总收入
| 椅子 | 表格 | 收入 |
| 0 | 54 | 1,080美元 |
| 24 | 四十八 | 1,200美元 |
| 四十八 | 24 | 960美元 |
| 60 | 0 | 600美元 |


