请问巫师 #267
如果您不确定答案,那么在游戏节目《百万美元大洒千里》中分配资金的最佳策略是什么?
为了其他读者的利益,让我先回顾一下规则。
- 一支球队的起步资金为 1,000,000 美元。
- 团队需要回答一道选择题。
- 团队要把钱分给所有可能的答案。所有投在正确答案上的钱都会进入下一个问题。
- 团队必须完全排除至少一个可能的答案,不投入任何资金。
- 这个过程重复几轮。玩家也有一次改变主意的机会。
显然,如果团队确定答案,那么他应该把所有钱都押在正确答案上。如果团队能把答案缩小到两个,但每个答案都有50%的正确概率,那么他们应该把钱平均分配给这两个选项。
如果团队倾向于某个答案,但又不完全排除其他一个或多个答案,情况就会变得更加困难。我们来看一个例子。假设团队确定每个正确答案的概率如下:A 10%,B 20%,C 30%,D 40%。他们应该如何分配他的钱?
我认为答案是遵循凯利准则。简而言之,团队应该在每次提问时最大化其财富对数。要做到这一点,你必须考虑你已经拥有多少财富。
假设您现有的财富(独立于节目本身积累)为 100,000 美元。这是您的第一个问题,因此您需要分配 1,000,000 美元的游戏节目奖金。首先,排除概率最低的选项,以符合节目规则。然后,您需要最大化 0.2×log(100,000+b*1,000,000) + 0.3×log(100,000+c*1,000,000) + 0.4×log(100,000+d*1,000,000),其中小写的 a、b 和 c 分别代表每个答案的分配比例。
这可以用微积分和解三项式方程、反复试验,或者我更喜欢用Excel的“目标搜索”功能来解答。无论你用什么方法,正确答案都是B占18.9%,C占33.3%,D占47.8%。
当然,节目里没人能在规定时间内完成所有这些数学题,更别提你还得在这段时间内转移一大堆现金。我更实际的建议是,根据你对答案正确概率的评估来分配资金,假设最不可能的选项不存在。在这个例子中,B选项分配22.2%,C选项分配33.3%,D选项分配44.4%。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
我听说过一家赌场,如果庄家爆牌,他会假定所有未出牌的玩家都赢了。游戏发牌时牌面朝上,但双倍下注的牌面朝下。所以,如果双倍下注的牌导致玩家爆牌,而庄家也爆牌,那么玩家就赢了。赌场这样做是因为他们担心算牌者,不想让玩家看到他们认为无关紧要的牌。在这条规则下,正确的基本策略是什么?赌场优势又是什么?
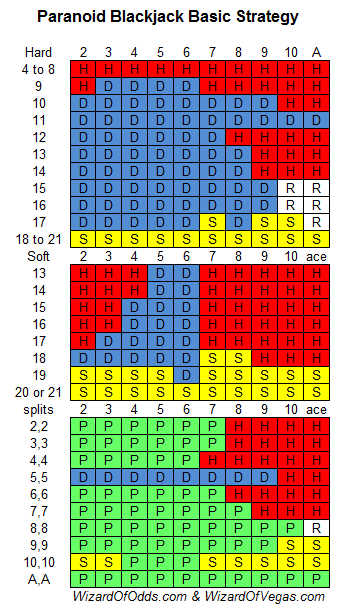
我假设有六副牌,庄家拿到软17,分牌后加倍,投降,然后重新分牌。如果不允许小牌加倍,那么我的玩家优势是4.9%。这是正确的策略。显然,这个策略可能会引发一些危险信号。
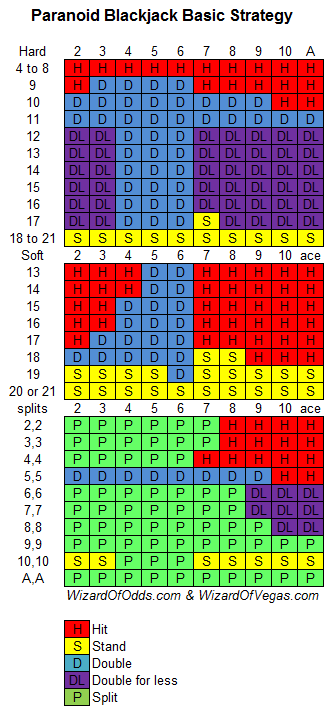
如果允许小额加倍,那么我采用以下策略可以获得最高9.4%的玩家优势。小额加倍时,尽量少下注,最好只加一分钱。我的9.4%是基于小额加倍下注的假设。实际上,大多数赌场都要求至少达到赌桌最低投注额才能加倍。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
在维也纳赌场,二十一点游戏有附加赌注。游戏使用六副牌,庄家在软17点时停牌。如果庄家爆牌,无论原始赌注结果如何,赔率为2赔5。
我的二十一点附录2B就是为这类问题而编写的。它显示,在这些规则下,庄家爆牌的概率是28.19%。也就是说,赌场优势是1.33%。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
您在2010年12月14日的专栏中写道,赌场特别提到的“AAAAAKK”牌型在扑克历史上可能从未出现过。据另一位荷官说,一位玩家在2010年11月在主街车站(Main Street Station)拿到了这手牌。
有意思。我之前写过,我估计内华达州每23.7年就会出现一次这种手。我想那次就是其中一次。


