请问巫师 #265
我试用了你们的精算计算器。为什么我达到预期死亡年龄的概率不到 50%?
你混淆了平均值和中位数。我们以我的情况为例。我是一名45岁的男性。我的预期寿命是78.11岁,但我活到80岁的概率是50.04%。
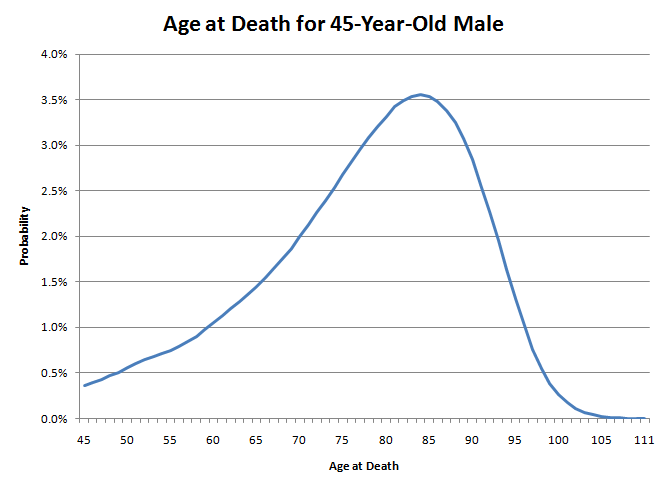
我的死亡年龄就像向这张图投掷飞镖一样。注意左尾比右尾粗得多。这意味着我现在死亡的概率很低。然而,随着年龄的增长,明年死亡的概率会越来越高。例如,对于一个45岁的男性来说,活到46岁的概率相当高,达到99.64%。然而,到了85岁,活到86岁的概率只有89.21%。这就像大自然慢慢地在你的背后捅刀子。起初它可能不会杀死你,但随着时间的流逝,它杀死你的概率会慢慢增加。然而,一旦你到了七十多岁后期,大自然就会对你不再玩命,开始真正地捅刀子。
因此,如果许多45岁的男性向这张图投掷飞镖,49.96%的人将在45岁至79岁之间命中,50.04%的人将在80岁至111岁之间命中。然而,幸运地落在图表右侧的那一半人可能活不过80岁。男性一旦达到80岁,预期寿命也只有7.78年。与此同时,那些不幸活不到80岁的人,许多人的寿命会比80岁短得多。因此,正是大量年轻人的死亡拉低了平均预期寿命。
对于类似的情况,考虑一个数字为 10、20、30、31、32、33 的骰子。平均值是 26,但掷出大于该值的概率为 2/3。
举个例子来说明平均值和中位数的不同之处,假设我们在样本中再增加两个死亡病例。一个在46岁时死亡,另一个在81岁时死亡。活到80岁的概率保持不变,但45岁时的平均预期寿命会下降。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
为什么赌场要费心列出用一对K分开五张A的例外情况?这种情况发生的频率有多高?如果发生,这种例外情况产生影响的概率有多大?
问得好。赌场规则是,五张A分开,低牌出两张A。例外情况是,如果你能出两张K,高牌中五张同点牌就保留。我的牌九扑克页面列出了拉斯维加斯和大西洋城的七种赌场规则,所有规则都包含这个例外。而这两座城市以外的三家赌场规则则没有。
拿到四张A、一张Jow和两张K的概率是25,690,513分之一。假设庄家押庄,这个例外唯一有用的情况是玩家的高牌是四张同点牌或更好的牌。这种情况的概率约为300分之一。两者同时发生的概率约为76亿分之一。
根据内华达州博彩管理委员会的数据,2009 年内华达州共有 306 张牌九扑克赌桌。如果我们慷慨地假设每小时 60 手,每桌两名玩家,每张赌桌全天候开放,那么这种例外情况需要 23.7 年才会发生,并对结果产生影响。
所以赌场要求每一位牌九扑克荷官记住这个例外,尽管它在游戏历史上可能从未对结果产生过影响。我猜想,提出增加这条规则的人,和决定将A2345顺子(即所谓的“轮盘”)定为第二大顺子的人是同一个人。
需要掷多少次骰子才能有 50/50 的概率掷出至少一个 12 点?
这是概率论史上的一个经典问题。很多人错误地认为答案是 18,因为掷出 12 的概率是 1/36,而 18×(1/36)=50%。然而,按照这个逻辑,掷 36 次得到 12 的概率应该是 100%,这显然不是。以下是正确答案。设 r 为掷骰次数。掷出非 12 的概率是 35/36。掷 r 次骰子中没有掷出 12 的概率是 (35/36) r 。因此,我们需要用以下公式解出 r:
(35/36) r = 0.5
对数(35/36) r = 对数(0.5)
r × log(35/36) = log(0.5)
r = log(0.5)/log(35/36)
r = 24.6051
所以没有一个整数答案。24次掷骰子中掷出12的概率是1-(35/36) 24 = 49.14%。25次掷骰子中掷出12的概率是1-(35/36) 25 = 50.55%。
如果你想押注,比如说你能在25轮中掷出12点,或者其他人在24轮中掷不出。无论哪种情况,你都能在均等投注中占据优势。
拉斯维加斯一家体育博彩公司公布的大学橄榄球比赛总分明显有误。市场数字是43,但他们开出的赔率是53。所以我押了大约20次小注,每次金额都很少,以免引起注意或影响赔率。不出所料,我赢了。现在我有点担心要不要把赌注提交给对方支付。赌场拒绝支付是否合理?
我赌10比1你一定会赢,尽管他们可能会先跟你聊几句。我之所以有些怀疑,是因为体育博彩公司在获得博彩管理委员会的许可后,可以撤销明显错误的投注。
“未经主席事先书面批准,博彩公司不得单方面撤销任何赌注。”——内华达州法规 22.115
虽然根据传闻证据,这项权利确实存在,但很少被援引。请告诉我发生了什么。
附言:提问者后来通知我,他很顺利地就拿到了报酬。
想象一条无限弹性的橡皮筋,未拉伸时长1公里。它以每秒1公里的速度膨胀。接下来,想象橡皮筋的一端有一只蚂蚁。当橡皮筋开始膨胀时,蚂蚁以相对于当前位置每秒1厘米的速度向另一端爬行。蚂蚁最终会到达另一端吗?如果会,什么时候?
是的, 100,000 -1秒后就会了。请参阅我的mathproblems.info网站,问题 206,其中有两个答案。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。


