请问巫师 #230
今天的新闻是，大西洋城的一名女子在Borgata 赌场连续掷骰子 154 次才掷出 7 点。这意味着她掷了 154 次骰子，没有一次掷出 7 点。所以我取 (30/36) 154 ，得出的概率超过 1.5 万亿分之一。赢得超级百万彩票的概率比连续掷 154 次非 7 点骰子马拉松的概率高出约 9,000 倍。考虑到这种情况发生的可能性微乎其微，而且人们被定罪的 DNA 证据中存在虚假匹配的概率仅为数十亿分之一，您会怀疑这是作弊行为吗？您会就此事咨询 Borgata 赌场吗？我已经打电话给他们，告诉他们我的名字，并告诉他们想怎么处理就怎么处理。我很想知道您的想法。
首先，她总共掷了 154 次骰子，第 154 次掷出了 7（ 来源：NJ.com ）。但是，这并不意味着她在前 153 次掷骰子中从未掷出过 7。她可以在 come out 掷骰子时掷出很多 7。正如我在2003 年 5 月 3 日的专栏中指出的那样，掷到第 154 次的概率是 56 亿分之一。赢得超级百万大奖的概率是 1 / (56,5)*46 = 175,711,536。因此，掷 154 次或更多次的难度大约是 32 倍。如果有足够的时间和表格（我认为是存在的），这样的事情迟早会发生。所以，我不会怀疑有人作弊。我粗略估计这种情况在任何一年发生的概率约为 1%。
另请参阅我在mathproblems.info上以矩阵表示的解决方案，问题 204。
Station Casinos 根据宾果游戏玩家的消费金额，向其提供免费的“Mini X”宾果卡，具体如下：
消费 1-19 美元 = 1 张免费卡
消费 20-29 美元 = 2 张免费卡
消费 30-39 美元 = 3 张免费卡
消费 $40-$49 = 4 张免费卡
消费 50-59 美元 = 5 张免费卡
消费满 60 美元即可获得 6 张免费卡
每张卡片上有五个数字，分别对应BINGO中的一个字母。奖品如下：
封面卡上有 5 个数字 = 10,000 美元
6 个数字的封面卡 = 3,000 美元
封面卡上有 7 个数字 = 500 美元
如果没有人用 7 个或更少的数字覆盖，则第一个覆盖的玩家将获得 50 美元的安慰奖。
下表显示每张卡的基本奖金价值为 1/5 美分。
Mini X卡的预期价值
| 呼叫 | 支付 | 可能性 | 返回 |
| 5 | 10000 | 0.00000006 | 0.00057939 |
| 6 | 3000 | 0.00000029 | 0.00086909 |
| 7 | 500 | 0.00000087 | 0.00043455 |
| 全部的 | 0.00000122 | 0.00188303 |
每张牌的安慰奖价值为50/n，其中n为参赛牌的数量。例如，如果有1000张参赛牌，那么每张牌的安慰奖价值为5美分。
在您的视频扑克双倍奖金扑克策略页面上，您声明如果您得到 5
6 7 8 9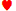
，持有顺子是正确的。这对我来说似乎违反直觉，但如果你能更详细地解释一下为什么持有同花顺是一个糟糕的策略，我将不胜感激。
在双倍奖金游戏中，同花顺赔率为 50，同花赔率为 6，顺子赔率为 4。凑成同花顺的概率为 2/47，凑成同花的概率为 7/47，凑成顺子的概率为 5/47。因此，弃掉 9 的预期回报为 (2/47)×50 + (7/47)×6 + (5/47)×4 = 3.4468。4 点顺子的预期收益要大得多。
拉斯维加斯的 3-5-7 纸牌游戏怎么了？我怎么也找不到。
我听说这款游戏因为侵犯了专利权，不得不从美国赌场下架。根据内华达州博彩管理委员会2008年第四季度的统计报告，以下是克拉克县的赌桌游戏数量。
克拉克县桌上游戏计数
| 游戏 | 表格 |
|---|---|
| 21 | 2537 |
| 轮盘赌 | 405 |
| 掷骰子 | 334 |
| 其他 | 243 |
| 百家乐 | 233 |
| 三张牌扑克 | 208 |
| 牌九扑克 | 194 |
| 迷你百家乐 | 143 |
| 任逍遥 | 98 |
| 牌九 | 80 |
| 命运之轮（六大） | 三十七 |
| 加勒比扑克 | 22 |
| 骰宝 | 1 |
| 恰克运气 | 1 |
不幸的是，他们没有说明这 243 款“其他”游戏是什么，所以这对回答您的问题没有多大帮助，但仍然值得一提。
先生，我玩了8672场自动单零轮盘游戏。我预设的号码竟然出现了278次。我选择这个号码是因为口袋的磨损。我怎么确定这个号码的概率高于1/37呢？
如果我的术语正确的话，“预测轮盘”是指根据球速、球位置和轮盘速度来预测球的落点。听起来你的做法是在利用偏向性轮盘，这是一种不同的优势玩法。既然我们讨论的是这个话题，那么第三种优势玩法就是利用“荷官签名”，荷官的玩法非常稳定，以至于每次旋转球和轮盘的速度几乎都相同。这使得玩家能够根据球的位置和过往结果来预测球的落点。
回答你的问题，你预期中奖的次数是 8672/37=234.38。方差是 8672×(1/37)×(36/37)=228.04。标准差是方差的平方根，即 15.10。你的中奖次数比预期多了 278-234.38=43.62。也就是 (43.62-0.5)/15.10 = 2.8556 个标准差。减去 0.5 的原因很难解释。简而言之，这是一个使用连续函数估计离散函数的调整因子。进行高斯近似，中奖次数达到或超过这个数字的概率是 0.21%。所以，你很有可能遇到了一个有偏差的轮盘。然而，仍有 1/466 的可能性，这只是运气好而已。