请问巫师 #227
三年前,您在“问问巫师”专栏中写道:“您说得对,500次掷骰子太少,不足以充分论证影响骰子结果的合理性,但500次掷骰子总比零次好。” 您能否描述一下,在实验中,您需要对所谓的骰子影响者进行哪些操作,才能让您有足够的信心开始对他进行大额投注?我之所以问这个问题,是因为在某些二十一点模拟游戏中,10亿轮掷骰子是“可靠”结果的良好基准。在最高效(即需要最少掷骰次数)的实验设计下,投掷者需要掷多少次才能确信自己能够影响结果?我知道答案取决于投掷者的技能,但您明白我的意思。即使在最好的情况下,如果也需要掷一百万次,那么这项尝试就不值得了。
信心的建立没有明确的标准,关键在于程度。首先,我会问测试的目的是什么,以及射手对结果的估计。任何测试都可能出现两种错误。一个熟练的射手可能会因为运气不好而失败,或者一个随机的射手可能会因为运气好而通过。在这两种情况下,我更倾向于避免假阳性。我认为合理的测试应该将假阴性的概率设定在5%左右,将假阳性的概率设定在1%左右。
例如,假设索赔人声称他平均每掷七次骰子就能掷出一个七。而随机掷骰子的人平均每掷六次就能掷出一个七。通过反复试验,我发现,要同时满足这两个条件,测试需要掷骰子3600次,并且需要547个或更少的七才能通过,或者每6.58次掷出一个七。
一位七分之一的射手平均应该能打出514.3个七分,标准差为21.00。使用高斯近似,这位技术娴熟的射手投出548个或更多七分(假阴性)的概率为5.7%。一位随机射手平均应该能打出600个七分,标准差为22.36。一位随机射手通过测试(假阳性)的概率为0.94%。下图显示了技术娴熟和随机射手的可能结果。如果结果在绿线左侧,那么我认为该射手通过了测试,我会押注他获胜。
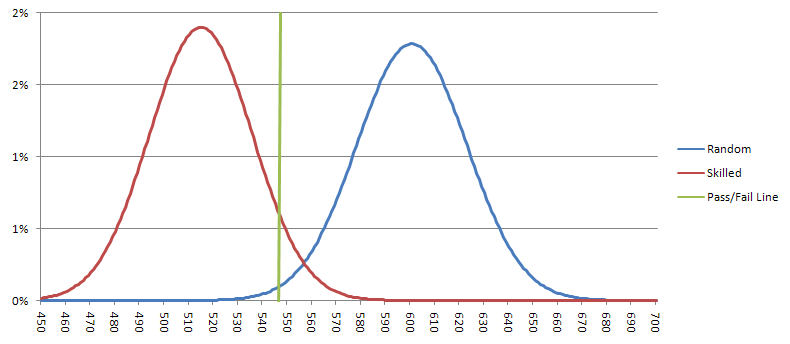
实际的难题是,如果我们假设每分钟投掷两次,那么进行测试将需要30个小时。或许我可以更自由地设定显著性水平,以减少时间要求,但结果可能不那么令人信服。我确实认为,现在是时候进行比500次投掷的黄氏实验更大规模的测试了。
如果“幸运女士”边注只在真实点数达到(比如说)10或以上时才进行,玩家能赢过赌场优势吗?如果能,那么最低真实点数是多少才能用这个边注赢过赌场优势?
我自己还没有研究过算牌对那个赌注的影响。不过,阿诺德·斯奈德研究过,他的研究成果可以在他的《二十一点大全》中找到。书中他提到,在六副牌的游戏中,如果最后两副牌的点数为+10或更大,使用红七点数,你就应该下注。在两副牌的游戏中,他建议用最后一副牌下注,并且点数为+6或更大。
如果庄家在6副牌的牌盒上允许玩家后期投降,如果庄家拿到软17点,如果庄家在软17点停牌,玩家能从中得到什么好处?如果是8副牌的牌盒呢?
类似问题的答案可以用我的赌场优势计算器来找到,只需修改一条规则,并记录对赌场优势的影响即可。通常我会让你这么做,但今天我比较耐心,所以就给你:
6副牌,庄家在软17点停牌:0.0726%
8副牌,庄家在软17点停牌:0.0758%
6副牌,庄家拿到软17点:0.0882%
8副牌,庄家拿到软17点:0.0916%
我想知道是否有办法计算出在百家乐中押注玩家时,从任何给定点平均需要多少次尝试才会输掉十个单位。
假设有八副牌,那么“闲”注的赌场优势为 1.2351%。预期输掉 10 个单位所需的手数为 10/0.012351 = 809.66。
最近我和家人在家玩扑克牌(奥马哈双双牌)。当时有五个人,最后只剩下两个人。我是其中之一。另一个人整晚都在赢。我终于拿到了一手好牌。我看了她一眼,嘲讽地叫了一声“四个七”。她说她有四张A,然后开始把筹码都掏走。然后我改口说我拿到了同花顺。她又说我已经跟注了四个七。我亮出了我的牌,她仍然坚持说我已经跟注了四个七,我的牌已经不行了。那么问题是谁赢了?显然,同花顺比四条强。但我说了那番话,是不是就弃牌了?钱还在桌上呢。
最终,牌会说话。你本应赢下这手牌。


