循环调度
本周的主题是如何安排循环赛。首先,我要先解释一下循环赛是一种比赛赛制,即每位选手与其他选手进行比赛。如果比赛有 n 位选手,比赛场次为 n(n-1)/2。
列出 n 位玩家的所有 n(n-1)/2 种可能的配对很容易。然而,理想情况下,每轮游戏一次,即每个玩家每轮玩一次。以下是如何在玩家人数为偶数的情况下做到这一点。我们以八人的情况为例。在下图中,我们将玩家标记为 A 到 H,并在四个矩形中显示两名玩家的比赛。这四场比赛将构成第一轮。注意每个人的比赛方式。
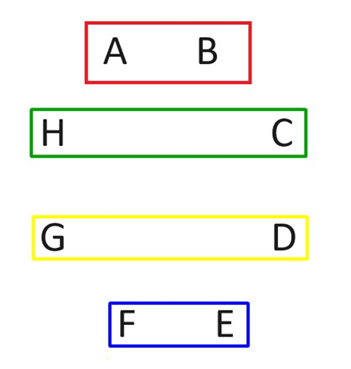
第二轮,保持玩家A的位置不变。然后其他人顺时针旋转,如下图所示。
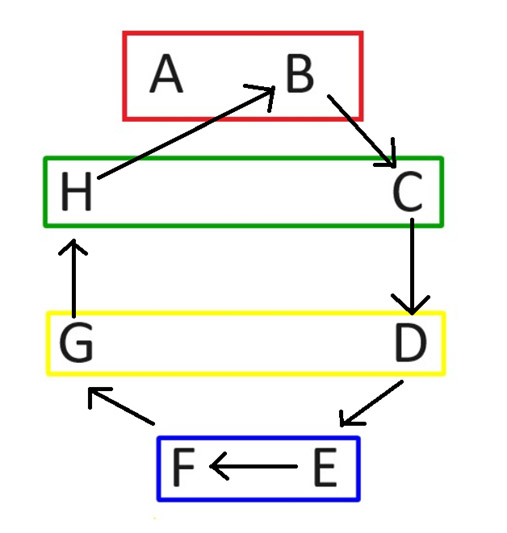
经过轮换,第二轮比赛安排如下:
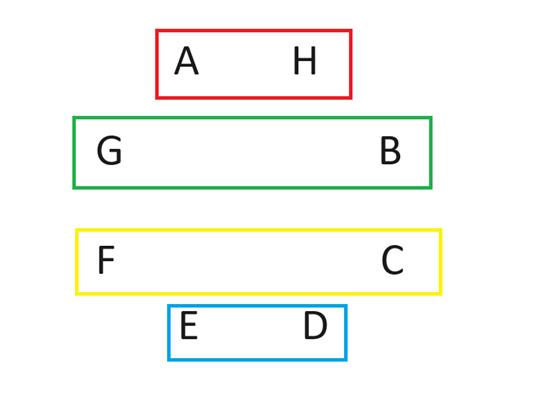
重复此操作,直到每个人都和玩家 A 交手。我无法解释为什么这种方法有效,但它确实有效。这种方法适用于任何偶数玩家。想了解更多相关讨论,请搜索“循环法”和“循环赛”。
下表列出了八人情况下的所有对阵情况。注意,每个人都只与其他人交手一次。
| 圆形的 | 玩家 1 | 玩家 2 |
|---|---|---|
| 1 | 一个 | B |
| 1 | 哈 | C |
| 1 | 格 | D |
| 1 | F | 埃 |
| 1 | 一个 | 哈 |
| 2 | 格 | B |
| 2 | F | C |
| 2 | 埃 | D |
| 3 | 一个 | 格 |
| 3 | F | 哈 |
| 3 | 埃 | B |
| 3 | D | C |
| 4 | 一个 | F |
| 4 | 埃 | 格 |
| 4 | D | 哈 |
| 4 | C | B |
| 5 | 一个 | 埃 |
| 5 | D | F |
| 5 | C | 格 |
| 5 | B | 哈 |
| 6 | 一个 | D |
| 6 | C | 埃 |
| 6 | B | F |
| 6 | 哈 | 格 |
| 7 | 一个 | C |
| 7 | B | D |
| 7 | 哈 | 埃 |
| 7 | 格 | F |
如果玩家人数为奇数,只需在锦标赛中添加一名虚拟玩家,即可获得偶数。与虚拟玩家对战的玩家将获得该轮轮空资格,这意味着该玩家无需参加比赛。因此,每个人都会有一轮轮空。以下是七人锦标赛的轮空规则。
| 圆形的 | 玩家 1 | 玩家 2 |
|---|---|---|
| 1 | 一个 | B |
| 1 | 再见 | C |
| 1 | 格 | D |
| 1 | F | 埃 |
| 2 | 一个 | 再见 |
| 2 | 格 | B |
| 2 | F | C |
| 2 | 埃 | D |
| 3 | 一个 | 格 |
| 3 | F | 再见 |
| 3 | 埃 | B |
| 3 | D | C |
| 4 | 一个 | F |
| 4 | 埃 | 格 |
| 4 | D | 再见 |
| 4 | C | B |
| 5 | 一个 | 埃 |
| 5 | D | F |
| 5 | C | 格 |
| 5 | B | 再见 |
| 6 | 一个 | D |
| 6 | C | 埃 |
| 6 | B | F |
| 6 | 再见 | 格 |
| 7 | 一个 | C |
| 7 | B | D |
| 7 | 再见 | 埃 |
| 7 | 格 | F |
最后,假设这是一场网球锦标赛,每个球场都有好球面和坏球面。坏球面可能朝向太阳。有什么公平的方法可以确保每个球员获得好球面和坏球面的次数相同?
为了解决这个问题,我提议使用《生活大爆炸》中解释的“蜥蜴史波克扩展”。这种石头剪刀布的玩法适用于任何奇数个符号。为了公平地确定哪位玩家拿到了好牌,我们考虑七人的情况。下图显示了哪位玩家拿到了好牌,箭头指向拿到坏牌的玩家。
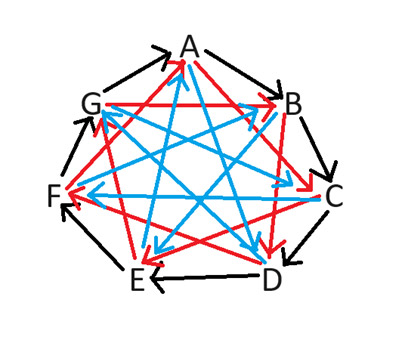
例如,如果玩家 B 和 D 玩牌,B 会占好牌,因为他们之间的箭头指向 D。不难看出我是如何画图的。箭头总是顺时针方向。我们需要为从 1 到 3 的所有可能的空位数都画出箭头。
然而,我们不需要画出这样的图,只需要画一个字母环即可。考虑两种顺时针绕圈从一个玩家到另一个玩家的方法。步数较少的路线将获得好方。考虑B和F之间的一局游戏。顺时针方向,从B到4需要四步,从F到B需要三步。由于三小于四,所以F获得好方。
下表显示了七人循环赛中所有可能的对阵情况,包括哪些球员占据优势,哪些球员占据劣势。
| 圆形的 | 好的一面 | 坏的一面 |
|---|---|---|
| 1 | 一个 | B |
| 1 | C | 再见 |
| 1 | D | 格 |
| 1 | 埃 | F |
| 2 | 一个 | 再见 |
| 2 | 格 | B |
| 2 | C | F |
| 2 | D | 埃 |
| 3 | 格 | 一个 |
| 3 | F | 再见 |
| 3 | B | 埃 |
| 3 | C | D |
| 4 | F | 一个 |
| 4 | 埃 | 格 |
| 4 | D | 再见 |
| 4 | B | C |
| 5 | 埃 | 一个 |
| 5 | D | F |
| 5 | 格 | C |
| 5 | B | 再见 |
| 6 | 一个 | D |
| 6 | C | 埃 |
| 6 | F | B |
| 6 | 格 | 再见 |
| 7 | 一个 | C |
| 7 | B | D |
| 7 | 埃 | 再见 |
| 7 | F | 格 |
不幸的是,这种平衡策略在玩家人数为偶数时不起作用。这是因为当两名玩家位于圆圈正对面时,圆圈周围的距离是相同的。如果必须如此,可以将这种方法用于所有其他比赛,但玩家必须在圆圈上相距180度时随机分配。
我暂时就此话题进行探讨。我保留在未来的新闻通讯中进一步阐述的权利。未来可能讨论的主题包括三名或三名以上球员的比赛,以及使用多块球场以平衡每位球员在每块球场上的出场频率。
最后,祝大家光明节快乐!


