能被 3 整除的证明
本周我打算暂时放下总统冷知识,尝试一些新的东西。我一直很喜欢数学证明。在灵感枯竭之前,我会讲解一些著名的数学定理,并尽可能用通俗易懂的方式解释它们的正确性。首先,本周我将证明:如果一个整数的各位数字之和能被3整除,那么这个整数本身也能被3整除。不过,在此之前,我先奉上每周例行的逻辑谜题。
逻辑谜题
桌上有四张牌。你可以看到正面朝上的牌分别标有 D、K、3 和 7。你知道每张牌的一面是字母,另一面是数字。据说有一条生产规则:一面是 D 的牌,另一面必须是 3。为了验证这条规则是否得到遵守,你需要翻开哪两张牌?
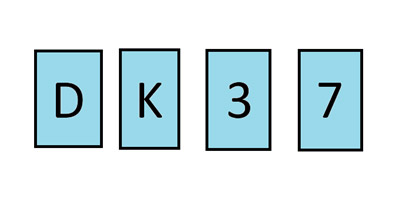
答案将在简报末尾揭晓。
能被 3 整除的证明
如引言所述,可以按如下方式检验一个整数是否能被 3 整除:
- 求各位数字之和。
- 如果根据规则 1 计算出的和能被 3 整除,那么原数也能被 3 整除。同样地,如果和不能被 3 整除,那么原数也不能被 3 整除。
例如,我们来看白宫的电话号码,即 2024567041。这几个数字之和为 2+0+2+4+5+6+7+0+4+1 = 31。31 不能被 3 整除,因此原号码也不能被 3 整除。
为了证明这种方法有效,请按如下方式分解原始数字:
6; font-family: 'Open Sans', sans-serif; color: #313131 !important; ">2024567041 = (2*1000000000) + 0 + (2*10000000) + (4*1000000) + (5*100000) + (7*1000) + 0 + (4*10) + (1*1)接下来,将 10 的幂分成两部分,一部分是 1,另一部分是其余部分:
= (2*(999999999+1)) + 0 + (2*(9999999+1)) + (4*(999999+1)) + (5*(99999+1)) + (7*(9999+1)) + 0 + (4*(9+1)) + (1*(0+1))
显然,任何由 9 组成的数字都能被 3 和 9 整除。例如,99999 = 3 * 33333。
也就是说,让我们重新排列上面数字中的各项。
= (2*999999999) + (2*9999999) + (4*999999) + (5*99999) + (7*9999) + (4*9) + (1*0) + (2*1) + (2*1) + (4*1) + (5*1) + (7*1) + (4*1) + (1*1)
前七项中的每一项显然都能被 3 整除,因为它们都能被一个由 9 组成的数整除。换句话说,(2*999999999) + (2*9999999) + (4*999999) + (5*99999) + (7*9999) + (4*9) + (1*0) 能被 9 整除,所以我们可以去掉 9 的部分。剩下:
(2*1) + (2*1) + (4*1) + (5*1) + (7*1) + (4*1) + (1*1) = 2+0+2+4+5+6+7+0+4+1 = 31
这是各位数字之和,等于 31。由于剩余部分不能被 3 整除,所以整个数字也不能被 3 整除。
这条规则同样可以用来判断一个数是否能被9整除。如果一个数的各位数字之和能被9整除,那么这个数也能被9整除。反之亦然,如果一个数的各位数字之和不能被9整除,那么这个数也不能被9整除。
逻辑谜题解答
我们将 3 必须位于 D 规则的对面这一规则称为“D-3”规则。
- • 很明显,我们必须翻开D牌,以确保另一面是3。
- • K 卡的背面必须有数字。由于对方不可能有 D,所以这张牌并不能帮助我们反驳 D-3 规则被遵守的事实。
- • 卡片背面必须有一个字母。如果这个字母是 D,则符合 D-3 规则。如果背面是其他字母,则对我们没有帮助。因此,这张卡片要么符合 D-3 规则,要么无关紧要。无论如何,我们正在寻找一张违反该规则的卡片,以使 D-3 规则失效。背面的任何字母都无法推翻 D-3 规则,因此无需检查。
- • 7号牌的另一面必须有一个字母。如果这个字母是D,那么这张牌就推翻了D-3规则。因此,必须检查它是否是D-7牌,因为D-7牌与D-3规则相矛盾。
因此,只有 D 和 7 这两张牌需要检查。


