在这一页
有机轮盘实验
简介
2016年9月,我听到有人指控Interblock生产的有机轮盘赌机对轮盘计时玩家采取了激进的反制措施。作为一名公平公正博彩的倡导者,这个话题引起了我的关注。在六个月的时间里,我参加了许多关于这个话题的会议,收集了数千次旋转的数据。本页讲述了调查的经过。
游戏
有机轮盘机在拉斯维加斯的许多赌场都有。它的运作方式与赌桌游戏相同。玩家大约有30秒的时间下注。通常情况下,球会在玩家还剩1到5秒的时间时射出。下注结束后,球还需要几秒钟才能落地。然后,赢家将获得赔付,整个过程将重复进行。从开始到结束大约需要一分钟多一点的时间。
指控
如果从球发射到投注结束之间有足够的时间,就有可能赢得比赛。投注结束前可以分析球和轮盘的速度。轮盘计时员可以估算球发射时的速度、轮盘的位置,从而预测球最终会落在轮盘的哪个位置。
我将提到这个问题的玩家称为S先生。据他所说,娱乐型玩家可能觉得游戏公平,因为每个号码的中奖概率是1/38。然而,如果出现某些危险信号,游戏就会进入他所说的“威胁模式”。对于轮盘赌玩家来说,危险信号通常包括:
- 大额赌注。“大额”的定义尚不明确,但总计 20 美元被认为足够了。
- 后期投注。具体来说,就是从球发出到时间窗口关闭之间的五秒钟。
- 区域投注。对轮盘上相邻的单个数字进行投注。
据称,如果游戏感到受到威胁,机器就会采取激进的反制措施。这些反制措施的目的是让球落到轮盘计时员所设定的区域之外。具体是如何做到的尚不清楚,但 S 先生有一些理论,他让我不要透露。
S先生与我分享了他的数据和分析,这绝对足以激起我的好奇心。然而,S先生要求我不要透露任何细节。
全球游戏博览会
在我参与此事的早期阶段,我参加了2016年在拉斯维加斯举办的全球游戏博览会。Interblock在那里占据了一个非常宽敞醒目的位置。在S先生的鼓励下,我请求与Interblock展位的一位工程师交谈。最初与我互动的女销售员找到了一位工程师,他走了过来并做了自我介绍。我坐在一台类似于有机轮盘赌的机器前,这台机器在球发射后也允许玩家在大约五秒钟内完成下注。介绍完毕后,我们的对话如下,我转述如下:
- 沙克尔福德:我注意到在这台机器上,球在投注停止前几秒钟就被释放了。
- Interblock:然后呢?
- 沙克尔福德:你不认为它容易受到计时轮盘团队的攻击吗?
- Interblock:我们很清楚这个问题。
他的肢体语言和语气表明他不想再说了,所以我感谢他抽出时间,然后高高兴兴地继续前行。
按照你的想法来理解这次谈话。
第一次实验
在听完S先生的演示后,我非常好奇到底发生了什么。首先,我和另一位感兴趣的人(我称之为C先生)收集了299次旋转的数据。我们的投注方式是每次在五个连续的数字上投注2美元。S先生不确定总共10美元的投注是否足以让游戏感到威胁,但他觉得在激怒游戏和在实验过程中不损失太多钱之间取得了良好的平衡。
我和C先生都不是玩轮盘赌的人,所以我们会系统地投注,把投注弧的中心点作为第二轮的获胜数字。我们的目标是看看轮盘上的获胜位置与我们投注弧的中心点相比如何。
图 1 和表 1 显示了我们的中心投注位置和中奖号码之间的每次偏移频率。
png" />表 1
| 抵消 | 观察 | 期望 |
|---|---|---|
| -18 | 5 | 7.87 |
| -17 | 9 | 7.87 |
| -16 | 十三 | 7.87 |
| -15 | 7 | 7.87 |
| -14 | 11 | 7.87 |
| -13 | 12 | 7.87 |
| -12 | 7 | 7.87 |
| -11 | 10 | 7.87 |
| -10 | 8 | 7.87 |
| -9 | 10 | 7.87 |
| -8 | 6 | 7.87 |
| -7 | 8 | 7.87 |
| -6 | 9 | 7.87 |
| -5 | 10 | 7.87 |
| -4 | 3 | 7.87 |
| -3 | 7 | 7.87 |
| -2 | 7 | 7.87 |
| -1 | 6 | 7.87 |
| 0 | 8 | 7.87 |
| 1 | 4 | 7.87 |
| 2 | 4 | 7.87 |
| 3 | 8 | 7.87 |
| 4 | 7 | 7.87 |
| 5 | 4 | 7.87 |
| 6 | 18 | 7.87 |
| 7 | 6 | 7.87 |
| 8 | 9 | 7.87 |
| 9 | 6 | 7.87 |
| 10 | 8 | 7.87 |
| 11 | 4 | 7.87 |
| 12 | 十三 | 7.87 |
| 十三 | 3 | 7.87 |
| 14 | 8 | 7.87 |
| 15 | 12 | 7.87 |
| 16 | 6 | 7.87 |
| 17 | 7 | 7.87 |
| 18 | 9 | 7.87 |
| 19 | 7 | 7.87 |
| 全部的 | 299 | 299.00 |
卡方拟合优度检验结果显示,卡方统计量为45.29,自由度为37。随机游戏产生比此更偏斜结果的概率为16.5%。
表2显示了在第一次实验中,以中心数字投注为中心的各种弧长进行高斯检验的结果。对于我们涵盖的五个数字的弧长,公平轮盘的预期中奖次数为39.3次。我们实际中奖次数只有29次。在公平游戏中,出现如此糟糕或更差结果的概率为3.84%。
表 2
| 圆弧尺寸 | 观察 | 期望 | 标准尺寸 偏差 | 标准数量 偏差 | 可能性 |
|---|---|---|---|---|---|
| 1 | 8 | 7.87 | 2.77 | 0.05 | 0.518957 |
| 3 | 18 | 23.61 | 4.66 | -1.20 | 0.114658 |
| 5 | 二十九 | 39.34 | 5.85 | -1.77 | 0.038417 |
| 7 | 四十四 | 55.08 | 6.70 | -1.65 | 0.049187 |
| 17 | 124 | 133.76 | 8.60 | -1.14 | 0.128074 |
虽然我们的结果确实低于预期,但这也可能只是普通的运气不好。不过,我计算了一下,如果我一直以同样的速度输,就需要更大的样本量来证明游戏不公平。经过多次会议和邮件沟通,我们决定进一步进行第二次实验。
第二次实验
为了证明赌场游戏不公平,必须进行可重复的实验来证明这一点。经过大量讨论,我们决定测试在五个数字组成的弧线中每个数字下注5美元,以判断是否存在赢钱不足的情况。我们决定在三个不同的轮盘上进行1000次旋转。除了S先生在场外,至少还有一位证人,要么是我,要么是C先生。我们决定在游戏结束后,检查数据并决定下一步行动。如果看起来我们玩的是非随机游戏,并且排除合理怀疑,我们计划公开证据。
故事结束时,我们收集了1204次旋转的数据。我们知道结果略低于预期,但据S先生说,游戏大多数时候表现都很随机,只有部分时间处于“受威胁”模式。
根据对数据的审查,我们认为我们的损失还不足以保证继续比赛。
以下是第二个实验的结果和分析。首先,下面的图表和表3显示了球落点与球的落点之间的每次偏移频率。
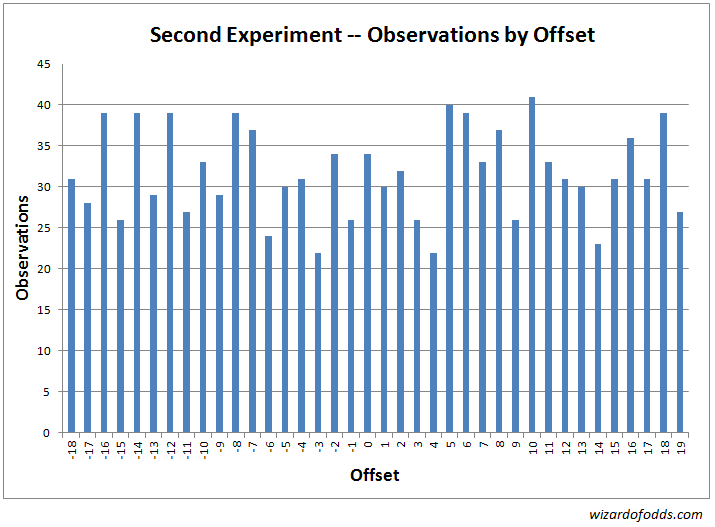
表 3
| 抵消 | 观察 | 期望 |
|---|---|---|
| -18 | 31 | 31.68 |
| -17 | 二十八 | 31.68 |
| -16 | 三十九 | 31.68 |
| -15 | 二十六 | 31.68 |
| -14 | 三十九 | 31.68 |
| -13 | 二十九 | 31.68 |
| -12 | 三十九 | 31.68 |
| -11 | 二十七 | 31.68 |
| -10 | 33 | 31.68 |
| -9 | 二十九 | 31.68 |
| -8 | 三十九 | 31.68 |
| -7 | 三十七 | 31.68 |
| -6 | 24 | 31.68 |
| -5 | 三十 | 31.68 |
| -4 | 31 | 31.68 |
| -3 | 22 | 31.68 |
| -2 | 三十四 | 31.68 |
| -1 | 二十六 | 31.68 |
| 0 | 三十四 | 31.68 |
| 1 | 三十 | 31.68 |
| 2 | 三十二 | 31.68 |
| 3 | 二十六 | 31.68 |
| 4 | 22 | 31.68 |
| 5 | 40 | 31.68 |
| 6 | 三十九 | 31.68 |
| 7 | 33 | 31.68 |
| 8 | 三十七 | 31.68 |
| 9 | 二十六 | 31.68 |
| 10 | 41 | 31.68 |
| 11 | 33 | 31.68 |
| 12 | 31 | 31.68 |
| 十三 | 三十 | 31.68 |
| 14 | 23 | 31.68 |
| 15 | 31 | 31.68 |
| 16 | 三十六 | 31.68 |
| 17 | 31 | 31.68 |
| 18 | 三十九 | 31.68 |
| 19 | 二十七 | 31.68 |
| 全部的 | 1204 | 1204.00 |
卡方拟合优度检验结果显示,卡方统计量为34.79,自由度为37。随机游戏产生比此更偏斜结果的概率为57.32%。
表4显示了以投注中心数字为中心的各种弧长的高斯检验结果。所有弧长均在正常范围内。
表 4
| 圆弧尺寸 | 观察 | 期望 | 标准尺寸 偏差 | 标准数量 偏差 | 可能性 |
|---|---|---|---|---|---|
| 1 | 三十四 | 31.68421053 | 5.55 | 0.42 | 0.661637 |
| 3 | 90 | 95.05263158 | 9.36 | -0.54 | 0.294599 |
| 5 | 156 | 158.4210526 | 11.73 | -0.21 | 0.418235 |
| 7 | 204 | 221.7894737 | 13.45 | -1.32 | 0.092997 |
| 17 | 536 | 538.6315789 | 17.25 | -0.15 | 0.439385 |
综合结果
以下是第一次和第二次实验的综合数据。首先,下图和表5显示了弧线中心与球落地位置之间每次偏移的频率。
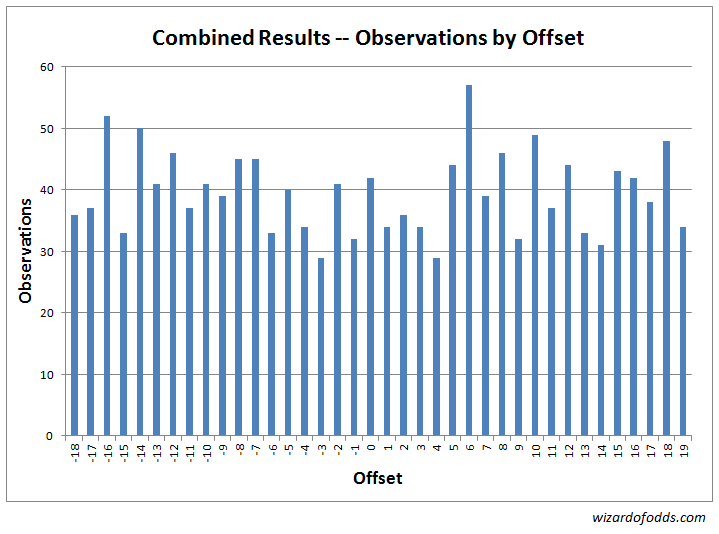
表 5
| 抵消 | 观察 | 期望 |
|---|---|---|
| -18 | 三十六 | 39.55 |
| -17 | 三十七 | 39.55 |
| -16 | 52 | 39.55 |
| -15 | 33 | 39.55 |
| -14 | 50 | 39.55 |
| -13 | 41 | 39.55 |
| -12 | 46 | 39.55 |
| -11 | 三十七 | 39.55 |
| -10 | 41 | 39.55 |
| -9 | 三十九 | 39.55 |
| -8 | 45 | 39.55 |
| -7 | 45 | 39.55 |
| -6 | 33 | 39.55 |
| -5 | 40 | 39.55 |
| -4 | 三十四 | 39.55 |
| -3 | 二十九 | 39.55 |
| -2 | 41 | 39.55 |
| -1 | 三十二 | 39.55 |
| 0 | 四十二 | 39.55 |
| 1 | 三十四 | 39.55 |
| 2 | 三十六 | 39.55 |
| 3 | 三十四 | 39.55 |
| 4 | 二十九 | 39.55 |
| 5 | 四十四 | 39.55 |
| 6 | 57 | 39.55 |
| 7 | 三十九 | 39.55 |
| 8 | 46 | 39.55 |
| 9 | 三十二 | 39.55 |
| 10 | 49 | 39.55 |
| 11 | 三十七 | 39.55 |
| 12 | 四十四 | 39.55 |
| 十三 | 33 | 39.55 |
| 14 | 31 | 39.55 |
| 15 | 43 | 39.55 |
| 16 | 四十二 | 39.55 |
| 17 | 三十八 | 39.55 |
| 18 | 四十八 | 39.55 |
| 19 | 三十四 | 39.55 |
| 全部的 | 1503 | 1503.00 |
卡方拟合优度检验结果显示,卡方统计量为41.75,自由度为37。随机游戏产生比此更偏斜结果的概率为27.19%。
表6展示了以投注中心数字为中心的不同弧长进行高斯检验的结果。所有测试结果均在公平游戏的合理范围内。
表 6
| 圆弧尺寸 | 观察 | 期望 | 标准尺寸 偏差 | 标准数量 偏差 | 可能性 |
|---|---|---|---|---|---|
| 1 | 四十二 | 39.55263158 | 6.21 | 0.39 | 0.653346 |
| 3 | 108 | 118.6578947 | 10.45 | -1.02 | 0.153986 |
| 5 | 185 | 197.7631579 | 13.11 | -0.97 | 0.165050 |
| 7 | 248 | 276.8684211 | 15.03 | -1.92 | 0.027374 |
| 17 | 660 | 672.3947368 | 19.28 | -0.64 | 0.260114 |
第一次实验和第二次实验结果之间的相关系数为 0.153853。简单来说,这意味着存在轻微的相关性,但完全在两组随机数据的预期范围内。
结论
我需要非常高标准的证据才能断言任何游戏没有按照公平游戏的自然概率进行。在本案中,这一标准并未得到满足。换句话说,我没有理由指责有机轮盘赌机的玩法不公平。
回应
在向公众发布之前,我邀请 S 先生预览一下这个页面。他提出了很多很好的建议和修改意见。但最终,他对我的措辞还是有些意见。所以我给了他发表回复的机会,他也照做了。回复的标题是《S 先生对Interblock 实验结果的另一种看法》。
我总是喜欢说最后一句话,所以我发表了一篇反驳文章,题为《对 S 先生对迈克尔·沙克尔福德的有机轮盘实验的回应》 。



